Die Lichtbrechung bzw. die Brechung des Lichts (auch Refraktion genannt) ist ein Phänomen, das auftritt, wenn eine Welle am Übergang in ein anderes Medium ihre Wellengeschwindigkeit ändert.
Da sich Licht wie eine Welle verhält, ändert sich die Ausbreitungsgeschwindigkeit des Lichts z.B. beim Übergang von Luft zu Wasser oder umgekehrt. Brechung kommt bei allen Arten von Wellen vor: Licht, Schallwellen, Wasserwellen, Erdbebenwellen etc.
Die Lichtbrechung ist die Grundlage für Linsen, mit welchen Lichtstrahlen gezielt gesammelt oder gestreut werden können.
Das Wichtigste in Kürze
Wenn das Licht an der Grenzfläche zweier transparenter Medien von einem Medium in ein anderes übertritt, erfolgt Brechung des Lichtstrahls. Sie ist eine direkte Folge der unterschiedlichen Wellengeschwindigkeiten des Lichts in den beiden Medien.
Das Brechungsgesetz sagt uns, unter welchem Winkel ein Strahl gebrochen wird. Dabei ist \(\alpha_1\) der Einfallswinkel zum Lot auf die Grenzfläche im Medium 1 (Brechungsindex \(n_1\)) und \(\alpha_2\) der Brechungswinkel im Medium 2 mit \(n_2\).
Brechungsgesetz Formel:
\[ \frac{\sin(\alpha_1)}{\sin(\alpha_2)} = \frac{n_2}{n_1} \]
Trifft der Strahl senkrecht auf die Grenzfläche (Einfallswinkel \(\alpha_1 = 0^\circ\)), dann ist der Brechungswinkel ebenfalls \(\alpha_2 = 0^\circ\).
Je grösser der Brechungsindex, desto langsamer ist das Licht im entsprechenden Medium und desto kleiner ist der Einfallswinkel bzw. Brechungswinkel in diesem Medium, d.h. der Strahl ist im langsameren Medium steiler zur Grenzfläche als im schnellen Medium.
Beim Übergang von einem Medium mit grösserem Brechungsindex in ein optisch weniger dichtes Medium gibt es den Extremfall, in welchem der Brechungswinkel 90° beträgt. Ab diesem Punkt tritt Totalreflexion auf.
Häufigste Fragen
Lichtbrechung an der Grenzfläche
“Der Lichtstrahl wählt jenen Weg, für welchen er zwischen zwei Punkten eine extremale Zeit benötigt (maximal oder minimal).”
Im Bild oben sehen wir, wie der Lichtstrahl beim Eintreffen ins Glas einen charakteristischen “Knick” macht und seine Richtung ändert.
Der Einfallswinkel (zum Lot) ist in der Luft grösser als der entsprechende Winkel im Glas. Dieser “Knick” ist eine Folge des Fermat’schen Prinzips. Gemäss diesem Gesetz wählt das Licht im Fall der Brechung den Weg mit minimaler Laufzeit.
Mit Hilfe der Brechungsindizes wird die Wellengeschwindigkeit im Medium berechnet: Je grösser der Brechungsindex, desto langsamer ist das Licht im entsprechenden Medium.
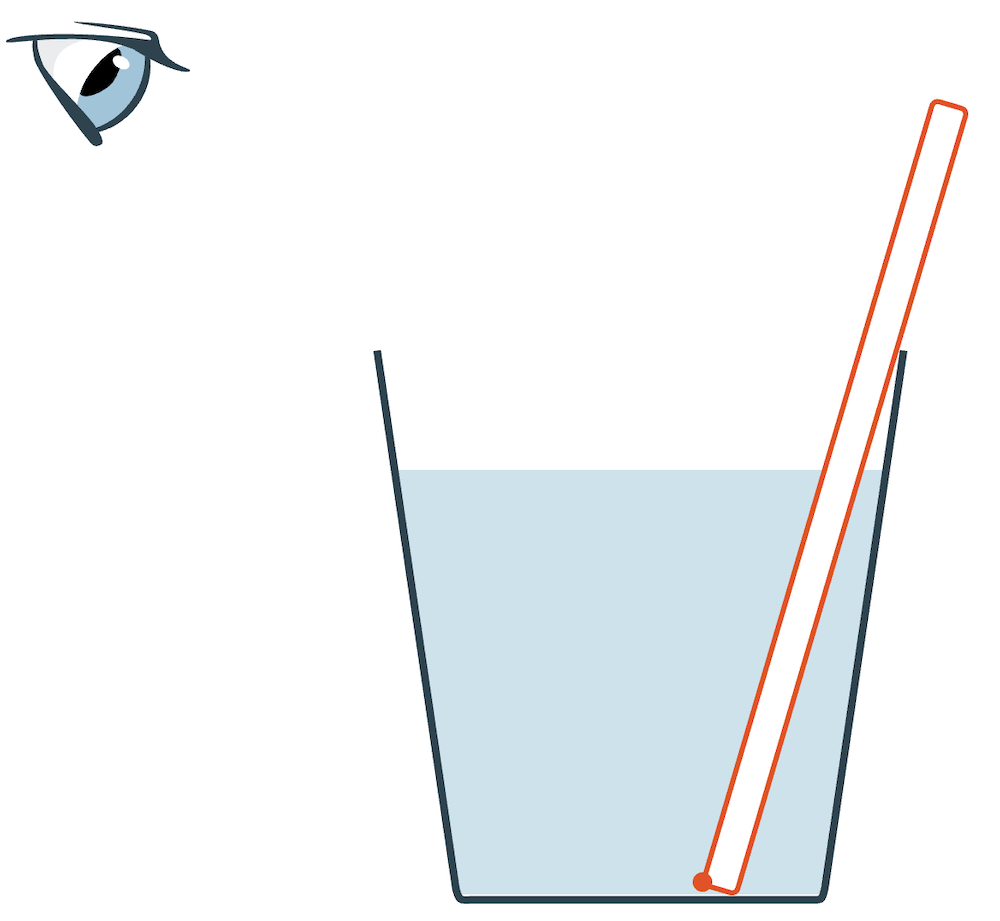
Beispiel: Lichtbrechung eines Strohhalms im Wasser
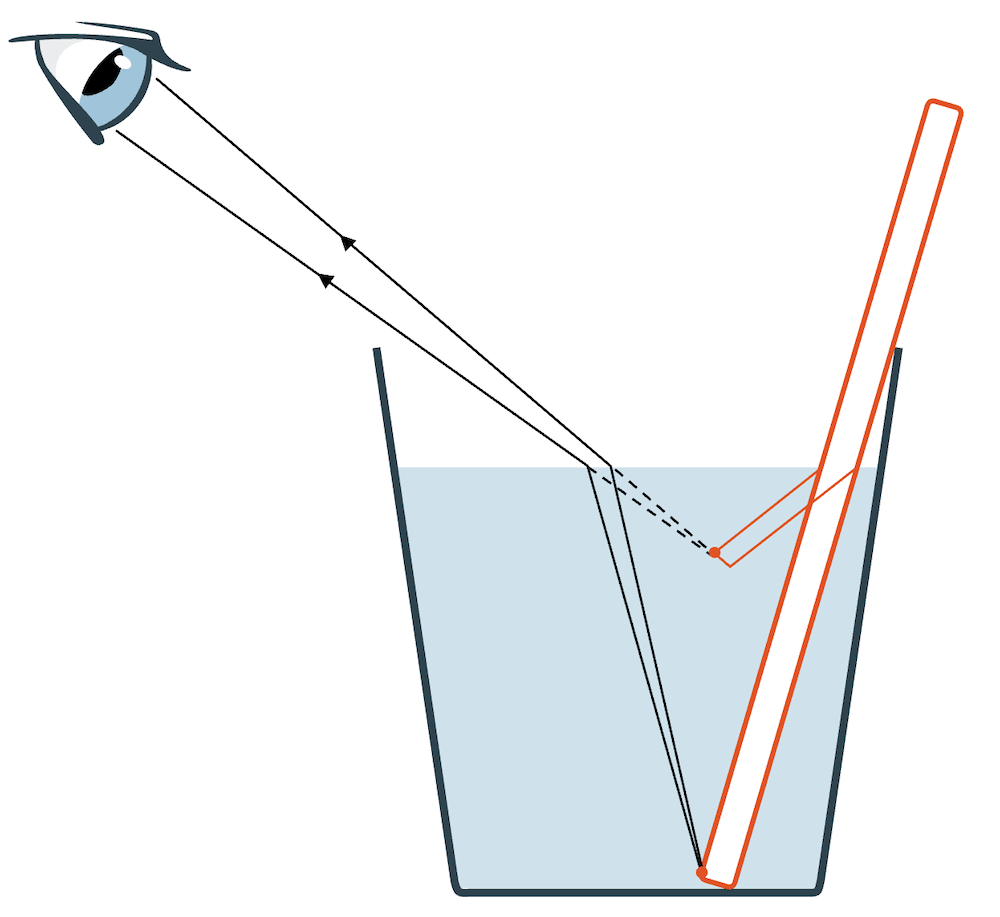
Der Betrachter sieht einen geknickten Strohhalm. Zeichne einen denkbaren Verlauf für zwei gestreute Lichtstrahlen, ausgehend vom Punkt am Ende des Strohhalms. Wie sieht der Beobachter diesen Punkt?
Durch die Brechung von Licht in Wasser bei der Grenzfläche zu Luft entsteht ein Knick.
Der Brechungsindex Wasser (\(n_{Wasser} \approx 1.33\)) ist grösser als der Brechungsindex Luft (\(n_{Luft} \approx 1\)), d.h. Licht ist im Wasser langsamer als in der Luft. Dadurch nimmt das Licht im Wasser einen, bezüglich der Grenzfläche steileren Weg ein, als in der Luft.
Der Beobachter sieht einen virtuellen Bildpunkt weiter oben im Wasser. Dadurch erscheint der Strohhalm verkürzt und zum Beobachter hin geknickt.
Brechungsgesetz
Das Brechungsgesetz nach Snellius beschreibt den Einfalls- und Brechungswinkel im jeweiligen Medium in Abhängigkeit der Brechungsindizes \(n_1\) (Medium 1) und \(n_2\) (Medium 2):
\[ \frac{\sin(\alpha_1)}{\sin(\alpha_2)} = \frac{n_2}{n_1} \]
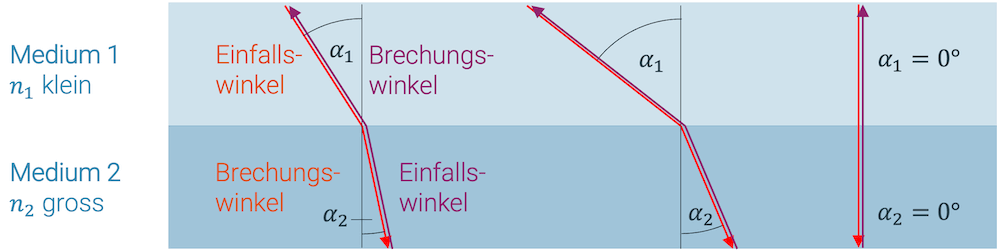
Beachte, dass das Gesetz für beide Laufrichtungen des Lichts gilt: Der Winkel \(\alpha_1\) ist der Einfalls- oder Brechungswinkel im Medium 1, je nach Laufrichtung.
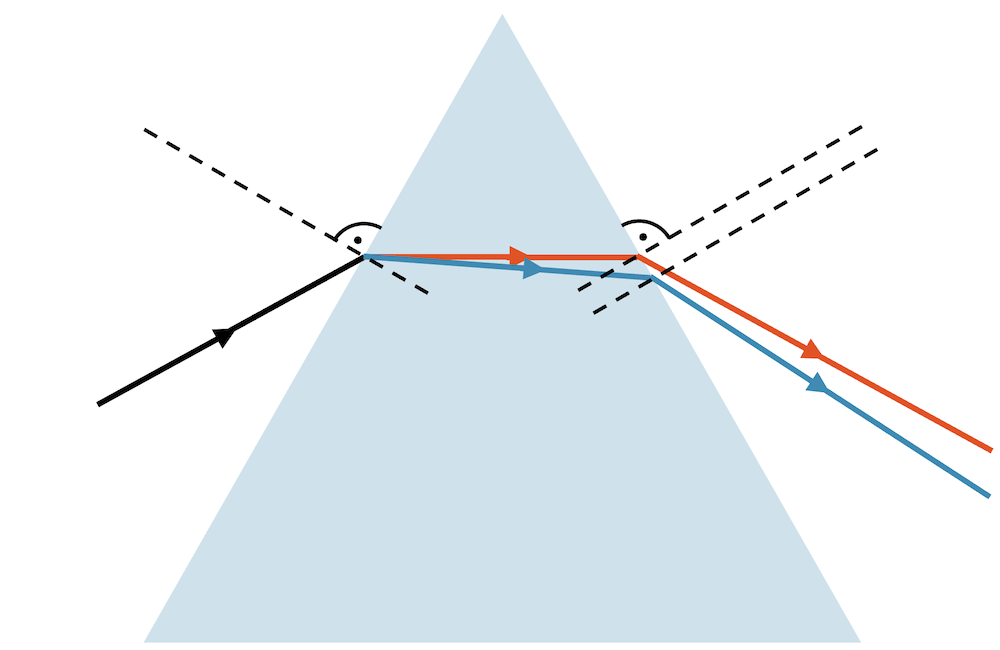
“Je grösser sich die beiden Brechungsindizes unterscheiden, desto stärker ist der Knick. Ein Übergang in ein anderes Medium mit (fast) gleichem Brechungsindex findet praktisch ohne Brechung statt.”
Je grösser der Unterschied der beiden Brechungsindizes, desto stärker ist der “Knick”. Der langsamere Lichtstrahl nimmt gegenüber der Grenzfläche einen steileren Winkel ein als der schnellere Lichtstrahl.
Senkrecht einfallende Lichtstrahlen brechen nicht, da Einfalls- und Brechungswinkel beide \(\alpha_1\) = \(\alpha_2\) = 0 ° betragen.
Im Extremfall kann der grössere Winkel im Medium mit kleinerem Brechungsindex 90° erreichen. In diesem Fall kann der Lichtstrahl nicht mehr aus dem optisch dichteren Medium austreten und es tritt Totalreflexion auf.
Beispiel: Anwendung Brechungsgesetz
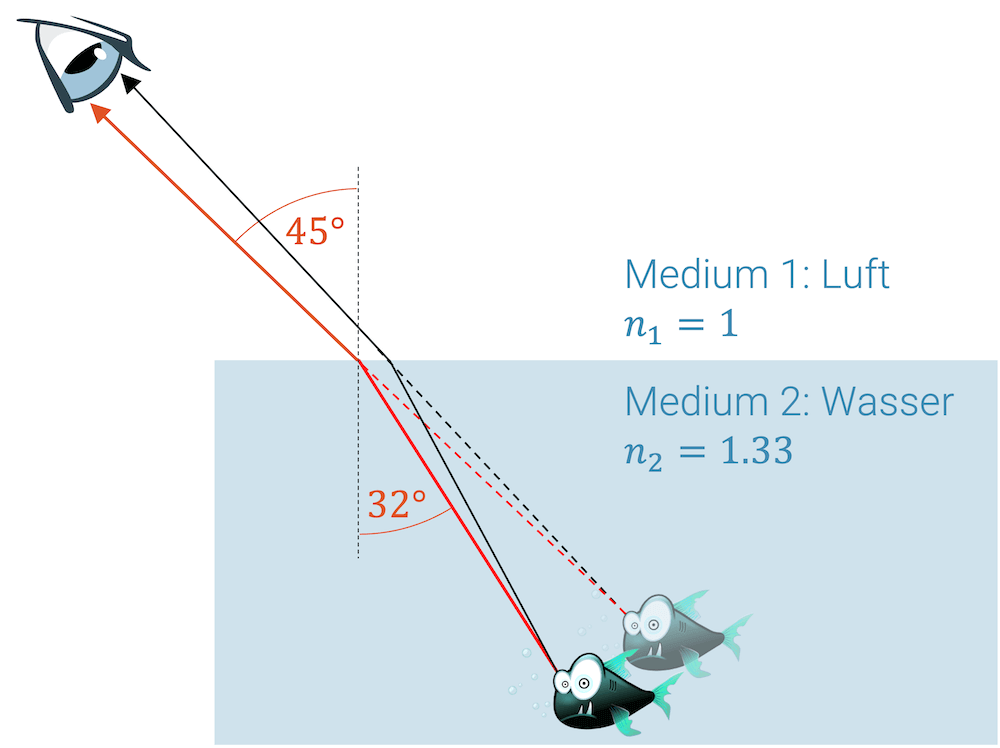
Ein Betrachter sieht einen Fisch unter einem Brechungswinkel von 45°.
Wie gross ist der Einfallswinkel im Wasser ()? Erscheint der Fisch weiter oben oder weiter unten im Wasser als er wirklich ist?
- Brechungsindex Luft: \(n_1\) = 1
- Brechungsindex Wasser: \(n_2\) = 1.33
Da der Betrachter immer annimmt, die vom Fisch kommenden Lichtstrahlen wären gerade, sieht er den Fisch weiter rechts und in geringerer Tiefe, als er wirklich ist.
Mit Hilfe des Brechungsgesetzes und den beiden Brechungsindizes \(n_1\)=1 für die Luft und \(n_2\)=1.33 für das Wasser, kann er den Einfallswinkel \(\alpha_2\) berechnen:
\[ \frac{\sin(\alpha_1)}{\sin(\alpha_2)} = \frac{\sin(45^\circ)}{\sin(\alpha_2)} = \frac{n_2}{n_1} = \frac{1.33}{1} \]
Wir lösen nach \(\sin(\alpha_2)\) auf:
\[ \sin(\alpha_2) = \frac{\sin(45^\circ)}{1.33} \]
Jetzt nehmen wir die Umkehrfunktion des Sinus (Arkussinus) auf beide Seiten der Gleichung und nutzen den Umstand aus, dass dadurch der Sinus links verschwindet:
\[ \arcsin(\sin(\alpha_2)) = \arcsin \left( \frac{\sin(45^\circ)}{1.33} \right) \]
\[ \alpha_2 = \arcsin \left( \frac{\sin(45^\circ)}{1.33} \right) \approx \underline{32^\circ} \]
Herleitung
Licht, das im Medium 1 auf eine Grenzfläche trifft, verhält sich wie eine Wellenfront mit der Wellenlänge \(\lambda_1\). Die Wellenfront trifft unter dem allgemeinen Einfallswinkel \(\alpha_1\) ein.
Da der Brechungsindex von Medium 2 grösser ist, als derjenige von Medium 1 (\(n_2 > n_1\)), ist die Welle im Medium 2 langsamer. Die regelmässig auf die Grenzfläche auftreffenden Wellenberge und -täler pflanzen sich im anderen Medium fort.
Durch die kleinere Wellengeschwindigkeit sind die Wellenberge und -täler aber näher zusammengerückt: Die Wellenlänge im Medium 2 ist kürzer als im Medium 1 (\(\lambda_2 < \lambda_1\)).
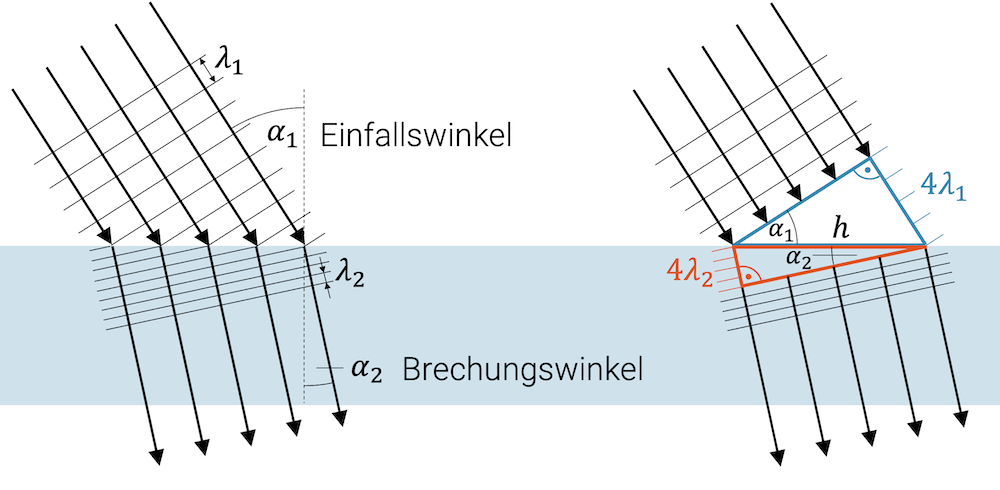
Betrachte nun die beiden rechtwinkligen Dreiecke in der Grafik rechts. Das blaue Dreieck hat eine Hypothenuse \(h\) und eine Gegenkathete mit der Länge von vier Wellenlängen \(4 \lambda_1\). Für den Einfallswinkel \(\alpha_1\) gilt deshalb:
\[ \sin(\alpha_1) = \frac{4 \lambda_1}{h} \]
Da der erste Strahl von links genau vier Wellenlängen früher auf die Grenzfläche auftrifft als der fünfte Strahl, ist er im Medium 2 auch schon vier Wellenlängen voraus, wenn der fünfte Strahl erst beginnt.
Die Gegenkathete im roten Dreieck beträgt ebenfalls vier Wellenlängen \(4 \lambda_2\) und es gilt analog:
\[ \sin(\alpha_2) = \frac{4 \lambda_2}{h} \]
Lösen wir die beiden Ausdrücke nach \(h\) auf, erhalten wir:
\[ h = \frac{4 \lambda_1}{\sin(\alpha_1)} = \frac{4 \lambda_2}{\sin(\alpha_2)} \]
Wir wissen, dass die Lichtgeschwindigkeit \(u_1\) im Medium 1 der Lichtgeschwindigkeit im Vakuum entspricht, die um den Faktor des Brechungsindex’ \(n_1\) verkleinert ist:
\[ u_1 = \frac{c}{n_1} \]
Ab dem Zeitpunkt, in welchem der erste Strahl von links auf die Grenzfläche trifft, verstreicht eine gewisse Zeit, bis auch der fünfte Strahl die Grenzfläche erreicht. Wir geben vor, diese Zeit zu kennen und schreiben für sie einfach \(\Delta t\).
Da die Welle in der Zeit \(\Delta t\) genau vier Wellenlängen \(4 \lambda_1\) kommt, können wir für die Wellengeschwindigkeit schreiben:
\[ u_1 = \frac{4 \lambda_1}{\Delta t} \]
Wir setzen beide Ausdrücke für die Wellengeschwindigkeit \(u_1\) gleich:
\[ \frac{c}{n_1} = \frac{4 \lambda_1}{\Delta t} \]
Nun können wir die obige Gleichung nach \(4 \lambda_1\) auflösen. Das Gleiche tun wir analog für das Medium 2. Wir erhalten somit:
\[ 4 \lambda_1 = \frac{c}{n_1} \cdot \Delta t \qquad \textrm{und} \qquad 4 \lambda_2 = \frac{c}{n_2} \cdot \Delta t \]
Eingesetzt in die Gleichung für die Hypothenuse ergibt:
\[ h = \frac{c \cdot \Delta t}{n_1 \cdot \sin(\alpha_1)} = \frac{c \cdot \Delta t}{n_2 \cdot \sin(\alpha_2)} \]
Nun lassen wir \(h\) weg, dividieren die Gleichung durch die Lichtgeschwindigkeit \(c\) und die Zeitperiode \(\Delta t\), so dass sie sich herauskürzen. Dann multiplizieren wir mit \(n_2\) und mit \(sin(\alpha_1)\). Wir erhalten so das Brechungsgesetz:
\[ \frac{\sin(\alpha_1)}{\sin(\alpha_2)} = \frac{n_2}{n_1} \]
Simulation
Weitere Links
Aufgabensammlung
Lernziele
- Du verstehst, dass der Ursprung der Lichtbrechung in der Änderung der Wellengeschwindigkeit des Lichts im betreffenden Material/Medium liegt. In Materialien mit einem grösseren Brechungsindex ist die Lichtgeschwindigkeit um diesen Faktor verlangsamt, im Vergleich zum Vakuum.
- Du kannst das Brechungsgesetz qualitativ und quantitativ anwenden, d.h. du kannst mit dem Brechungsgesetz rechnen und kannst aber auch Aussagen zur Grösse der Winkel machen, z.B. der Winkel muss grösser/kleiner sein, weil der Brechungsindex kleiner/grösser ist etc.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Kommentar oder Frage schreiben
Du musst angemeldet sein, um einen Kommentar abzugeben.