Auftrieb

Auftriebskraft

Den Effekt des Auftriebs erfahren wir durch das Auftreten einer Auftriebskraft \(F_A\), die nach oben zeigt. Diese Auftriebskraft bewirkt, dass z.B. ein Stück Holz oder ein Schiff im Wasser schwimmen. Auftrieb gibt es auch in Gasen. Er bewirkt, dass z.B. ein Ballon oder auch warme Luft aufsteigen.

In diesem Artikel geht es nur um den statischen Auftrieb. Die zweite Art von Auftrieb ist der dynamische Auftrieb, der z.B. an einem Flugzeugflügel entsteht.

Steigen und Sinken

Wenn ein Körper in ein Fluid (Flüssigkeit oder Gas) eingetaucht wird, erfährt er Auftrieb, d.h. es wirkt eine nach oben gerichtete Auftriebskraft \(F_A\).

Für einen leichten Körper ist die Gewichtskraft \(F_g\) klein und damit vielleicht sogar kleiner als die Auftriebskraft \(F_A\). In so einem Fall ist die resultierende Kraft \(F_res\) auf den Körper nach oben gerichtet und der Körper wird deshalb gemäss Newtons Zweitem Gesetz nach oben beschleunigt: Er steigt im Fluid auf (siehe Bild links).

Bei schweren Körpern ist die Gewichtskraft grösser als die Auftriebskraft und deshalb zeigt die resultierende Kraft nach unten. Sie macht, dass der Körper sinkt.

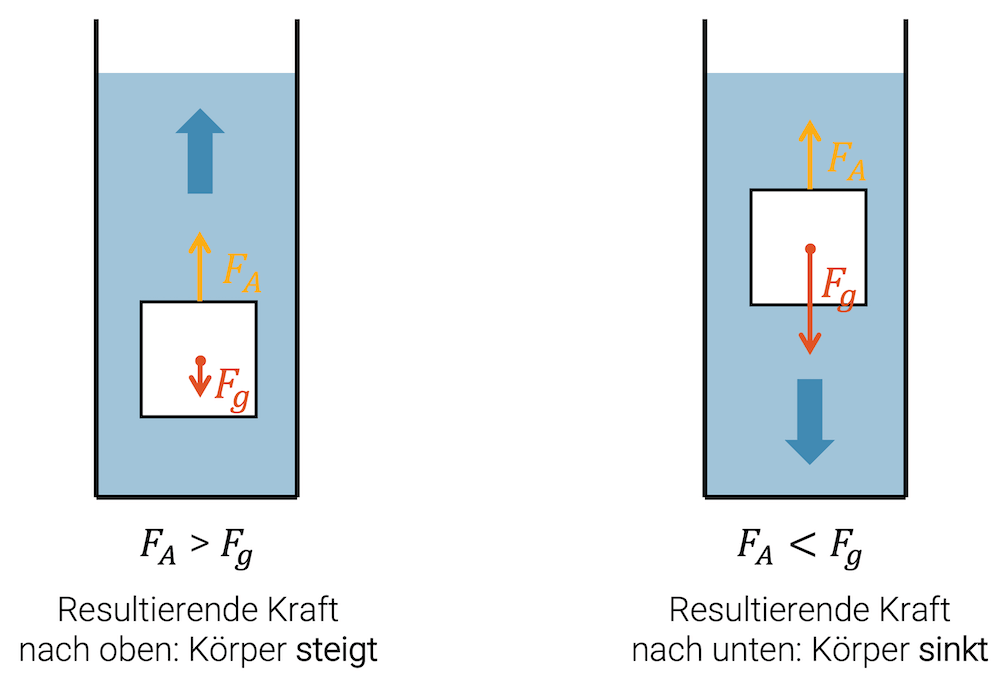
Beachte, dass die Auftriebskraft nur vom Volumen des Körpers abhängt, d.h. zwei gleich grosse Klötze werden die gleiche Auftriebskraft erfahren, egal ob sie aus ultraleichtem Balsaholz oder als Blei gefertigt sind.

Das genau gleiche Prinzip gilt auch bei Gasen: Ein Ballon ist “eingetaucht in Luft”. Er steigt auf, wenn die Auftriebskraft \(F_A\) grösser ist als seine Gewichtskraft \(F_g\).

Beachte: Ein Ballon, der gleich gross ist, wie ein Haus, wird die gleich starke Auftriebskraft erfahren, wie das Haus. Ja, auch die Auftriebskraft wirkt auch auf das Haus. Allerdings ist der Ballon so leicht, dass seine Gewichtskraft kleiner als die Auftriebskraft ist und er so fliegen kann.

Schweben und Schwimmen

In der Physik sagen wir: “Fische schweben. Nur tote Fische schwimmen.”

Wenn die Auftriebskraft gleich gross ist, wie die Gewichtskraft, heben sich beide Kräfte auf und wir haben Kräftegleichgewicht. Der Körper – in diesem Fall der Fisch – steigt weder auf, noch sinkt er ab. Er behält seine Position und schwebt.

Mit seiner Fischblase kann der Fisch sein Volumen leicht verändern und damit auch die Auftriebskraft leicht vergrössern oder verkleinern.

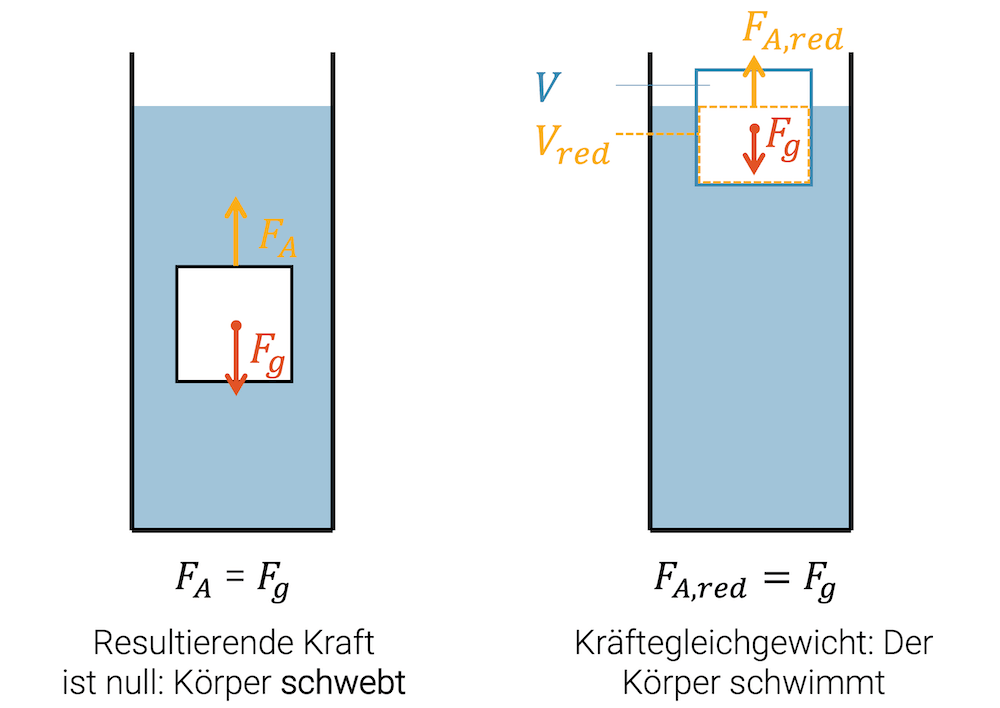
Wenn ein Körper leichter ist \((F_g < F_A)\), steigt er und schwimmt dann oben auf. Dabei ragt ein Teil des Körpers aus dem Fluid heraus, das für die Auftriebskraft verantwortlich ist.

Nun behält er seine Position und steigt nicht weiter auf, d.h. er ist jetzt im Kräftegleichgewicht.

Wie ist das möglich? Hatte er doch gerade vorhin noch kein Kräftegleichgewicht. Die Auftriebskraft \(F_A\) war grösser als die Gewichtskraft \(F_g\), was ihn ja zum Aufsteigen gebracht hat:

\[ F_A > F_g \]

Der Grund liegt darin, dass nur noch ein reduziertes Volumen \(V_{red}\) im Fluid eingetaucht ist.

Wenn die Auftriebskraft vom Volumen abhängig ist, dann ist diese Kraft bei kleinerem Volumen ebenfalls kleiner: Wir haben nunmehr eine reduzierte Auftriebskraft \(F_{A.red}\).

Der Körper ragt genau so viel aus der Flüssigkeit heraus, so dass das reduzierte Volumen \(V_{red}\) zu einer reduzierten Auftriebskraft \(F_{A,red}\) führt, die jetzt aber gleich gross ist, wie die Gewichtskraft:

\[ F_{A,red} = F_g \]

Beachte, dass der Teil des Körpers, der aus der Flüssigkeit herausragt, meistens in der Luft (oder sonst einem Gas) eingetaucht ist. Natürlich erfährt dieser Teil dadurch auch eine Auftriebskraft. Jedoch ist eine Auftriebskraft in einer Flüssigkeit immer viel grösser als eine Auftriebskraft in einem Gas. Wir können deshalb den Auftriebseffekt für das Stück, das herausragt, vernachlässigen.

Entdeckung des archimedischen Prinzips

Archimedes von Syrakus (287 v. Chr. – 212 v. Chr.) war ein griechischer Mathematiker, Physiker und Ingenieur und gilt als einer der bedeutendsten Mathematiker der Antike.

Der Legende nach soll der damalige König Hieron II ihn beauftragt haben zu testen, ob eine neu gefertigte Krone das ganze Gold beinhaltete, die der König einem Goldschmied in Auftrag gegeben hatte. Eine genaue Menge an Gold war dem Goldschmied übergeben worden und dieser kam eines Tages zurück mit der angefertigten Krone.

Hatte er wirklich alles Gold für die Krone verwendet? Natürlich zeigte die Krone das erwartete Gewicht auf der Waage. Vielleicht hatte der Goldschmied aber eine bestimmte Menge Gold mit der gleich schweren Menge an unedlem Metall ersetzt und im Inneren der Krone versteckt.

Archimedes sollte dies überprüfen, ohne jedoch die Krone in irgendeiner Weise aufzubohren oder sonst wie zu beschädigen.

Die Legende erzählt, dass Archimedes, in seiner Badewanne sitzend, plötzlich die entscheidende Idee hatte. Er soll nackt durch die Strassen von Syrakus gerannt und «Heureka!» geschrien haben, was “ich habe gefunden!” heisst.

Archimedes legte die Krone und die ursprüngliche Menge an Gold auf eine Balkenwaage. Da beide das gleiche Gewicht hatten, war die Waage im Gleichgewicht. Nun tauchte er die Waage mitsamt den Gewichten in Wasser ein.

Plötzlich zeigte die Waage ein Ungleichgewicht. Das Gold war jetzt scheinbar schwerer als die Krone.

Damit zeigte er, dass die Krone ein grösseres Volumen hatte als der Klumpen Gold. Wenn das Volumen grösser ist, obwohl die gleiche Masse sich darin befindet, muss die Dichte der Krone kleiner sein, als die Dichte von reinem Gold.

Die Krone bestand nicht mehr zu 100% aus Gold und Archimedes überführte so den betrügerischen Goldschmied.

Berechnung der Auftriebskraft – Archimedisches Prinzip

Bis hierhin wissen wir nur, dass die Auftriebskraft vom Volumen abhängt und dass sie bei Flüssigkeiten grösser ist als bei Gasen. Tatsächlich ist die Auftriebskraft proportional zum Volumen des Fluids, das durch den Körper verdrängt wird und ist auch proportional zur Dichte dieses Fluids.

Archimedisches Prinzip: Die Auftriebskraft \(F_A\) entspricht der Gewichtskraft \(\,F_g = m\,g\,\) des vom Körper verdrängten Fluids.

\[ F_A = m\,g = \rho_{Fl}\,V\,g \]

Dabei ist \(\rho_{Fl}\) die Dichte des Fluids und \(V\) das Volumen des Körpers.

Beachte auch, dass die Erdbeschleunigung \(g\) in der Formel vorkommt, d.h. bei Schwerelosigkeit haben wir keinen Auftrieb. Das ist eigentlich auch logisch, denn die Auftriebskraft zeigt nach oben. Bei Schwerelosigkeit gibt es kein “oben” und kein “unten” mehr.

Herleitung Auftriebskraft

Um die Auftriebskraft herzuleiten, betrachten wir einen einfachen Würfel, den wir in eine Flüssigkeit, z.B. Wasser, eintauchen. Wir wissen, dass die Wasserteilchen in Bewegung sind und somit einen Druck ausüben.

Aufgrund des Schweredrucks (hydrostatischer Druck) ist der Druck an der oberen Würfelfläche kleiner, als der Druck an der unteren Würfelfläche, weil wir dort in einer etwas grösseren Tiefe uns befinden.

\[ p_o = \rho_W\,g\,h_o, \quad p_u = \rho_W\,g\,h_u \]

Dabei ist \(\rho_W\) die Dichte von Wasser und \(h_o\) die Höhe der Wassersäule über der Würfelfläche oben und \(h_u\) die etwas grössere Tiefe für die untere Würfelfläche.

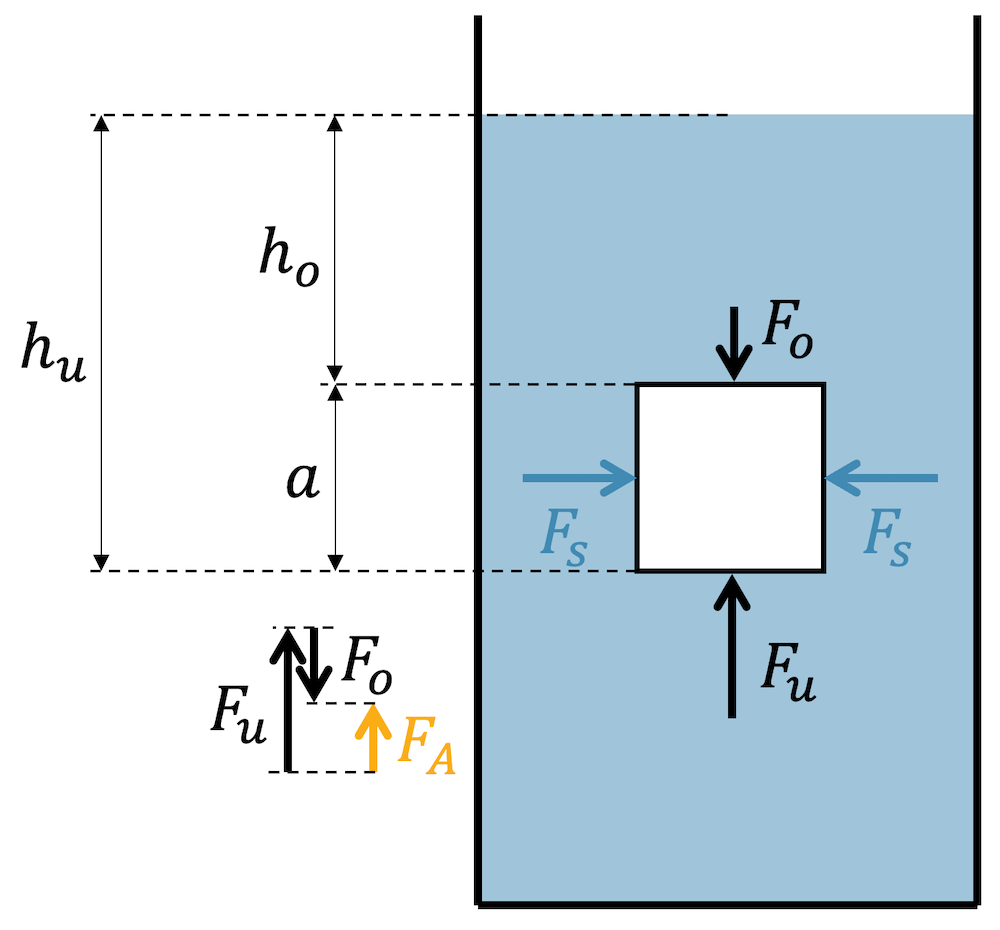
Der Druck wirkt mit einer Kraft auf die Würfelfläche, d.h. mit \(F_o\) oben und mit \(F_u\) unten.

Auf die Seitenflächen wirkt die Kraft \(F_S\) links und die gleich grosse Kraft \(F_S\) rechts. Aus Symmetrieüberlegungen gibt es keinen Grund, warum die eine Kraft grösser sein sollte als die andere. Beide Seitenflächen sind gleich gross und somit erwarten wir, dass beide Kräfte auch gleich gross sein sollten. Da sie einander entgegengesetzt sind, heben sie sich auf.

Mit der Fläche \(A\) erhalten wir die Kraft \(F_o\) bzw. \(F_u\). Wir wissen vom Schweredruck, dass die Höhe entscheidend ist. Somit muss \(p_u\) grösser sein als \(p_o\) und damit auch \(F_u > F_o\). Wir bilden deshalb die Differenz, die wir Auftriebskraft nennen:

\[ F_A = F_u – F_o = \rho_W\,g\,h_u \cdot A \; – \; \rho_W\,g\,h_o \cdot A \]

Jetzt können wir den gemeinsamen Faktor \(\rho_W\,g\,A\) ausklammern:

\[ F_A = (\rho_W\,g\,A) \cdot (h_u – h_o) \]

Wir nennen die Differenz der beiden Höhen \((h_u – h_o) = a\) und erhalten so:

\[ F_A = \rho_W\,g\,A\,a \]

Dabei ist das Produkt von Seitenfläche \(A\) und Seitenkante \(a\) gleich dem Volumen des Würfels: \(V=A\,a\).

Die Multiplikation der Dichte mit dem Volumen ergibt die Masse: \(m_W = \rho_W\,V\). Wir kriegen dann für die Auftriebskraft:

\[ F_A = m_W\,g \]

Links haben wir die Auftriebskraft \(F_A\) und sie entspricht der Gewichtskraft von Wasser! Wir sprechen hier aber nicht vom Wasser im Gefäss. Wir haben ja das Volumen des Würfels benutzt.

Es ist die Gewichtskraft des vom Würfel verdrängten Wassers.