Das Wichtigste in Kürze
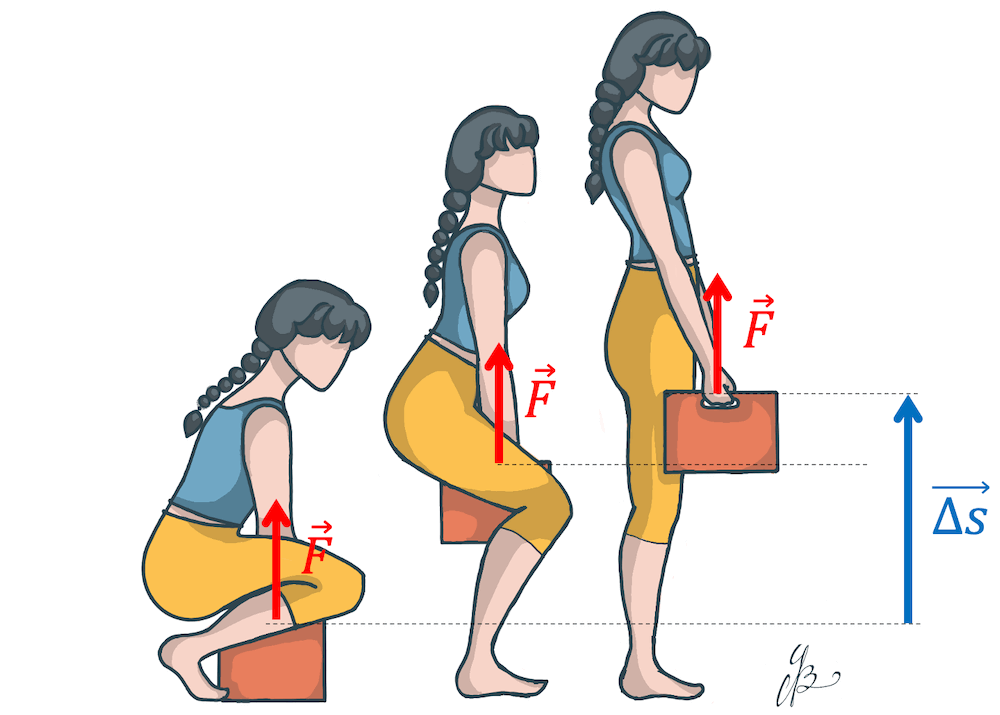
Die Hubarbeit ist eine Art von physikalischer Arbeit. Hubarbeit wird verrichtet, wenn eine Masse angehoben wird, d.h. entgegen der Gravitationskraft von der tieferen Lage auf Höhe $h_1$ auf eine höhere Lage bei Höhe $h_2$ gebracht wird.
Die verrichtete Hubarbeit ist nachher als potenzielle Energie gespeichert.
Hubarbeit Formel:
\[ W = m \cdot g \cdot h_2 – m \cdot g \cdot h_1 \]

Wenn wir für die Höhendifferenz (von \(h_1\) auf \(h_2\)) die Differenz \(\Delta h\) einsetzen, erhalten wir:
\[ W = m \cdot g \cdot \Delta h \]
Hubarbeit Beispiel: Pumpspeicherkraftwerk
Das Pumpspeicherkraftwerk Linth-Limmern (816 m.ü.M.) hat mehrere Speicherseen. Der höchst gelegene Muttsee liegt auf 2’446 m.ü.M. und fasst rund 9 Millionen Kubikmeter Wasser.
Wie viel Hubarbeit würde benötigt, um den Muttsee von einem Füllstand 50% auf 100% aufzufüllen?
Herleitung der Hubarbeit Formel
Für die physikalische Arbeit stellen wir die Grundgleichung auf:
\[ W=F \cdot \Delta s \]
Die Kraft, die aufgebracht werden muss, um eine Masse anzuheben, ist die Gewichtskraft. Wir ersetzen deshalb die Kraft \(F\) mit der Formel der Gewichtskraft \(F=F_g=mg\).
Die Höhe \(\Delta h\) ist die Wegstrecke \(\Delta s\) , die zu überwinden ist.
\[ \Delta s = \Delta h = h_2 – h_1 \]
Setzen wir den Ausdruck \(F=mg\) für die Kraft und \(\Delta s = h_2 – h_1\) für die Wegstrecke ein, erhalten wir den Ausdruck:
\[ W = mg \cdot (h_2 – h_1) = m \cdot g \cdot h_2 – m \cdot g \cdot h_1 \]
Aufgabensammlung
Weitere Links
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.