Wenn wir rechtwinklige Dreiecke analysieren, können wir mit den trigonometrischen Funktionen meistens alles berechnen. Leider sind die Dreiecke sehr oft nicht rechtwinklig. Mit dem Sinussatz können wir auch in einem allgemeinen Dreieck Gleichungen über die Winkel und Seitenlängen aufstellen und so, möglicherweise, das Dreieck berechnen.
In der folgenden Abbildung ist ein allgemeines Dreieck gezeichnet. Der Trick ist immer der Gleiche: Durch Einführen einer Höhe schaffen wir zwei rechtwinklige Dreiecke, für welche wir die trigonometrischen Funktionen hervornehmen können.
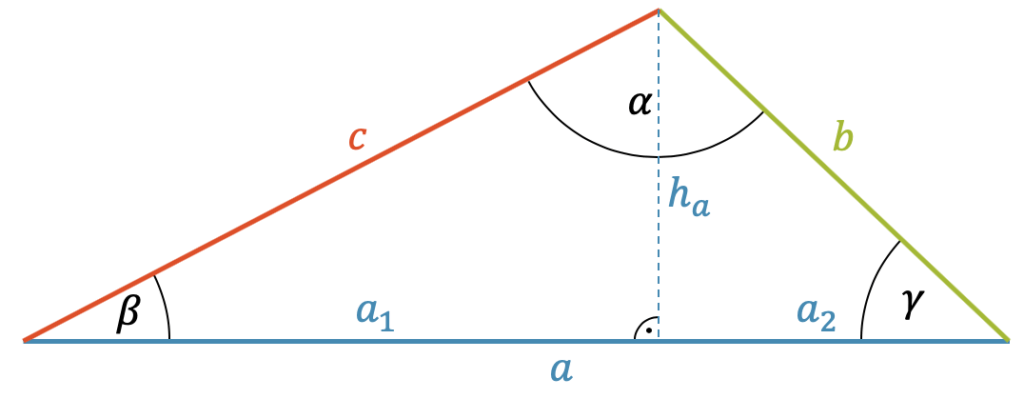
Wir stellen z.B. den Sinus für das linke und für das rechte rechtwinklige Dreieck auf:
\[ \text{links:}\;\;\sin(\beta) = \frac{h_a}{c} \quad \text{und} \quad \text{rechts:}\;\;\sin(\gamma)=\frac{h_a}{b} \]
Die Höhe \(h_a\) hat uns geholfen, rechtwinklige Dreieck zu erhalten. Wir kennen die Seiten nicht und mit der Höhe haben wir nur eine zusätzliche Unbekannte eingeführt. Allerdings haben wir jetzt zwei Gleichungen mit der gleichen Unbekannten \(h_a\) und können deshalb nach ihr auflösen und die beiden Gleichungen gleichsetzen, so dass \(h_a\) wieder verschwindet:
\[ h_a=c \cdot \sin(\beta) \quad \text{und} \quad h_a = b \cdot \sin(\gamma) \]
\[ c \cdot \sin(\beta) = b \cdot \sin(\gamma) \]
Jetzt dividieren wir durch \((bc)\) und erhalten:
\[ \frac{\sin(\beta)}{b} = \frac{\sin(\gamma)}{c} \]
Beachte, dass das Dreieck ein ganz allgemeines Dreieck war. Statt die Seiten \(a, b\) und \(c\) zu nennen, hätten wir sie ja auch \(b, c\) und \(a\) nennen können. Wir wenden die Umbenennungen \(a \rightarrow b\), \(b \rightarrow c\), \(c \rightarrow a\) und bei den Winkeln \(\alpha \rightarrow \beta\), \(\beta \rightarrow \gamma\) und \(\gamma \rightarrow \alpha\), auf die erhaltene Formel an und erhalten:
\[ \frac{\sin(\gamma)}{c} = \frac{\sin(\alpha)}{a} \]
Die Art, wie wir umbenannt haben, heisst zyklische Permutation. Sie ist in der Mathematik und Physik sehr üblich.
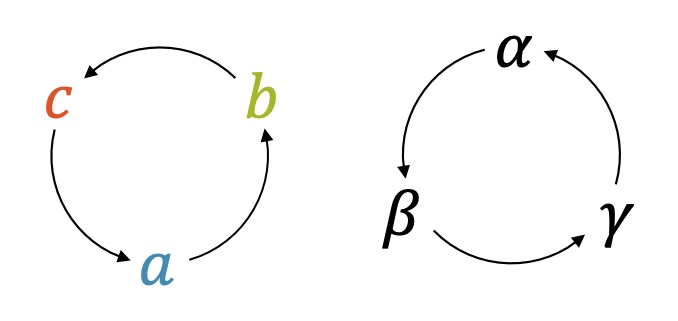
Schliesslich bilden wir den Kehrwert der Gleichung und erhalten:
Sinussatz:
\[ \frac{a}{\sin(\alpha)} \;\; = \;\; \frac{b}{\sin(\beta)} \;\; = \;\; \frac{c}{\sin(\gamma)} \;\; = \;\; 2R \]
Was wir an dieser Stelle nicht herleiten möchten, ist die Tatsache, dass die Brüche im Sinussatz auch mit dem Umkreisradius \(\boldsymbol{R}\) zusammenhängen, d.h. dem Radius des Umkreises um das Dreieck herum.
Beispiel
In einem Dreieck mit Seitenlänge a = 2.7 cm, sind die Winkel \(\alpha\)=116° und \(\beta\) = 26° gegeben. Wie gross sind die anderen Seiten?
Im Dreieck beträgt die Winkelsumme 180°, d.h. der dritte Winkel ist \(\gamma\) = 180°- 116° – 26° = 38°. Für die Seite \(b\) stellen wir den Sinussatz auf und lösen nach \(b\) auf:
\[ \frac{\sin(\beta)}{b} = \frac{\sin(\alpha)}{a} \]
\[ b = \frac{\sin(\beta)}{\sin(\alpha)} \cdot a = \frac{\sin(26°)}{\sin(116°)} \cdot 2.7\,\text{cm} \approx \underline{1.3\,\text{cm}} \]
Für die Seite \(c\) könnten wir analog vorgehen. Wir benutzen aber die zyklische Permutation und schreiben die Gleichung für \(b\) einfach um. Wir erhalten so direkt:
\[ c = \frac{\sin(\gamma)}{\sin(\beta)} \cdot b = \frac{\sin(38°)}{\sin(26°)} \cdot 1.3\,\text{cm} \approx \underline{1.8\,\text{cm}} \]
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.