Höhensatz

Der Höhensatz ist der zweite Satz in der Satzgruppe des Pythagoras. Er zeigt, wie die Höhe \(h\) die Grundseite in zwei Streckenabschnitte \(p\) und \(q\) aufteilt. Beachten Sie, dass es sich auch hier um ein rechtwinkliges Dreieck handeln muss.

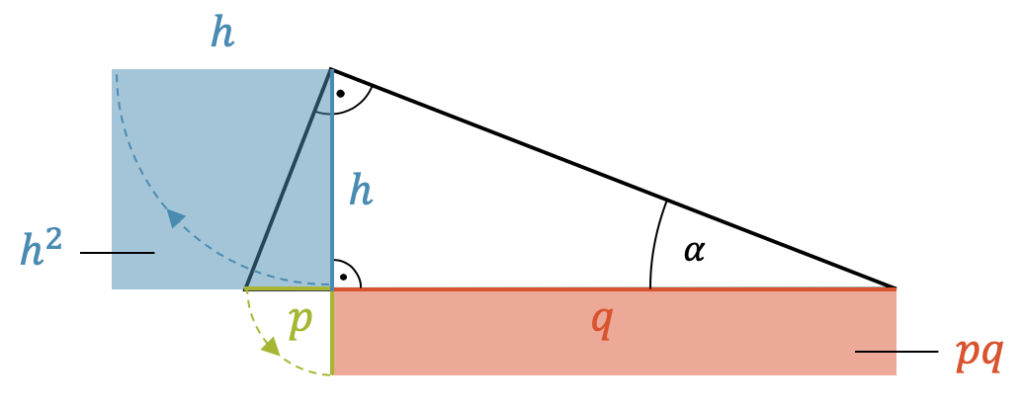
Wir können den Höhensatz wieder als Flächen darstellen. Für das Quadrat der Höhe \(h\) nehmen wir die Länge der Höhe in den Zirkel und tragen sie im rechten Winkel zur Höhe ab. Das Quadrat hat die Fläche \(h^2\).

Die Höhe \(h\) teilt die Grundseite in die beiden Streckenabschnitte \(p\) und \(q\). Wir machen jetzt das Gleiche mit dem Streckenabschnitt \(p\): Wir nehmen ihn in den Zirkel und tragen ihn senkrecht zu \(q\) ab. Damit erhalten wir ein Rechteck mit der Fläche \(p \cdot q\).

Die beiden Flächen in der Zeichnung sind, gemäss dem Höhensatz, gleich gross.

Beweis

Für den Beweis erinnern wir uns an die geometrische Ähnlichkeit. Die Höhe teilt nämlich das Dreieck in zwei Dreiecke.

Im linken Dreieck haben wir ganz links den Winkel \(\alpha’\). Rechts unten, am Fuss der Höhe, ist es natürlich ein rechter Winkel. Da die Summe alle Winkel in einem Dreieck \(180°\) ist, wissen wir, dass für den oberen Winkel \(\alpha\) gilt:

\[\alpha = 180° – \alpha’ – 90° = 90° –  \alpha’ \]

Der obere Winkel \(\alpha\) teilt den rechten Winkel des grossen ursprünglichen Dreiecks auf. Der Rest ist somit \(90° –  \alpha\) und das ist wiederum einfach \(\alpha’\), weil diese beiden Winkel zusammen \(90°C\) ergeben.

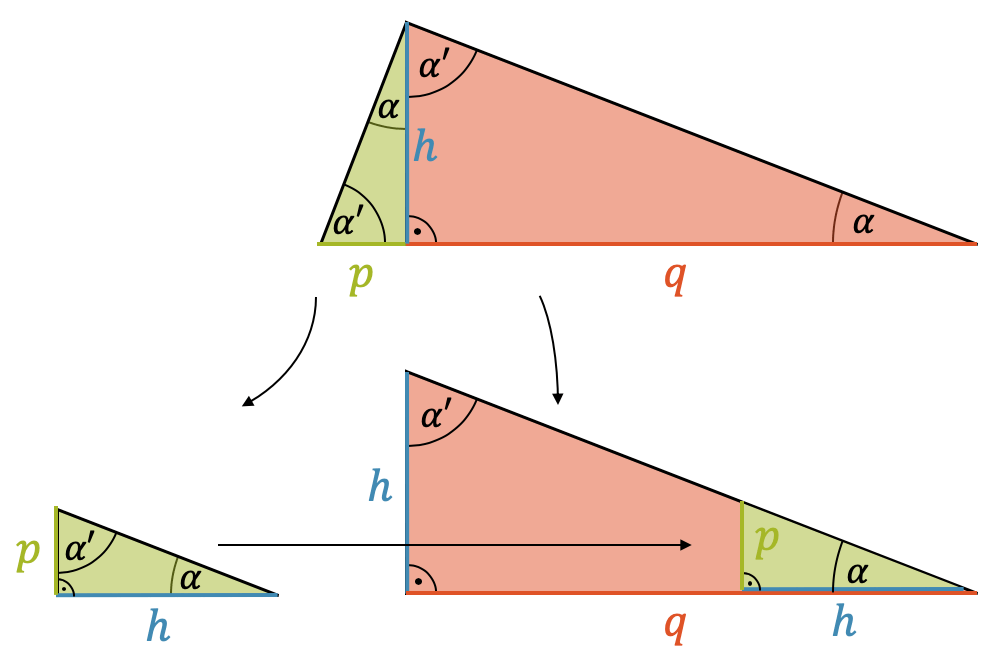
Das kleine Dreieck und das grosse Dreieck haben beide die Winkel \(\alpha’\) und \(\alpha\) und den rechten Winkel. Zwei Dreiecke, deren Winkel alle gleich sind, sind geometrisch ähnlich.

Wir wissen auch, dass für geometrisch ähnliche Figuren die Seitenverhältnisse proportional sind, wie uns das der Strahlensatz lehrt. Wir schauen uns beispielsweise das Verhältnis der kürzeren Kathete zur längeren Kathete an:

Im kleinen Dreieck ist die kürzere Kathete gleich dem Streckenabschnitt \(p\). Die längere Kathete ist die Höhe \(h\). Im grossen Dreieck haben wir die Höhe \(h\), die die kürzere Kathete bildet und der Streckenabschnitt \(q\) für die längere Kathete. Jetzt bilden wir die Verhältnisse als Bruch und setzen sie gleich:

\[\frac{p}{h} = \frac{h}{q} \]

Wir multiplizieren beide Seiten mit \(h\) und \(q\) und erhalten den Höhensatz

\[ \require{cancel} \frac{p}{\cancel{h}} \cdot \cancel{h}q = \frac{h}{\cancel{q}} \cdot h\cancel{q} \quad \rightarrow \quad pq = h^2 \]

Beispiel

Ein Tunnel hat den Querschnitt eines Halbkreises mit dem Radius \(r=4.35\,\text{m}\).

Wie hoch kann ein LKW der Breite \(b = 2.55\,\text{m}\) höchstens sein, wenn seine linke Seite \(30\,\text{cm}\) Abstand von der Tunnelmitte hat?

---

Wir machen eine Skizze des Tunnelquerschnitts und zeichnen den Lastwagen als Reckeck ein (blau).

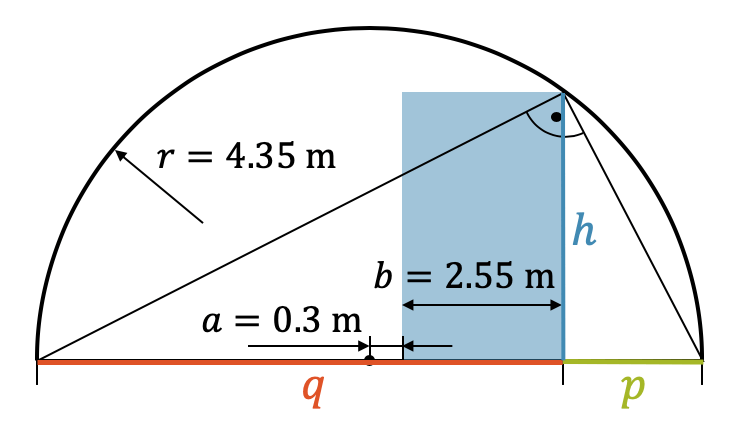
Wie immer bei der Anwendungen in der Satzgruppe des Pythagoras, brauchen wir ein rechtwinkliges Dreieck, um eine Gleichung aufzustellen. Hier bildet der Halbkreis einen Thaleskreis, d.h. wenn wir die Ecke des maximalen Lastwagens nehmen, die die Tunnelwand gerade berührt, so können wir von hier aus ein Dreieck bilden. Weil die Ecke auf dem Thaleskreis liegt, ist der Winkel automatisch ein rechter Winkel.

Die Höhe \(h\), die gesuchte Grösse, teilt die Grundseite in einen Streckenabschnitt \(p\) und \(q\). Mit Hilfe des Höhensatzes können wir \(h\) berechnen, wenn wir \(p\) und \(q\) kennen. Der Streckenabschnitt \(q\) setzt sich zusammen aus dem Radius \(r\), dem Abstand \(30\,\text{cm}\) und der Breite des Lastwagens.

\[q = 4.35\,\text{m} + 0.30\,\text{m} + 2.35\,\text{m} = 7.2\,\text{m} \]

Für den Streckenabschnitt \(p\) ist es einfach. Da \(p+q\) den doppelten Radius ergibt, können wir den eben berechneten Streckenabschnitt \(q\) abziehen:

\[p = 2r – q = (2 \cdot 4.35\,\text{m}) – 7.2\,\text{m} = 1.5\,\text{m} \]

Jetzt haben wir \(p\) und \(q\) und können den Höhensatz anwenden. Aus \(h^2 = pq\) machen wir \(h = \sqrt{pq}\):

\[h = \sqrt{pq} = \sqrt{1.5\,\text{m} \cdot 7.2\,\text{m}} = 3.28\,\text{m} \]

Beispiel

Konstruiere aus einem gegebenen gleichseitigen Dreieck ein flächengleiches Quadrat.

---

Das gleichseitige Dreieck hat drei gleiche Winkel von \(60°\). Es ist kein rechtwinkliges Dreieck und wir können so den Höhensatz noch nicht anwenden. Wenn wir aber eine Höhe einzeichnen, teilt sie das gleichseitige Dreieck in zwei rechtwinklige Dreiecke auf.

Wir wissen, dass die Höhe \(\frac{\sqrt{3}}{2}s\) beträgt. Die kurze Kathete beträgt \(\frac{s}{2}\). Multiplizieren wir die beiden Strecken, erhalten wir die Fläche eines Rechtecks.

\[A = \Big(\frac{\sqrt{3}}{2}s\Big) \cdot \Big(\frac{s}{2}\Big) \]

Dieses Rechteck hat die Fläche des gleichseitigen Dreiecks, denn wenn wir das Rechteck mit der Diagonale halbieren, erhalten wir zwei rechtwinklige Dreiecke, die zusammen wieder das gleichseitige Dreieck ergeben.

Im Höhensatz haben wir auch ein Rechteck, das die gleiche Fläche hat, wie das Quadrat aus der Höhe. Das Rechteck (mit Fläche \(pq\)) haben wir; das Quadrat (Fläche \(h^2\)) müssen wir konstruieren. Wir wählen die Höhe als unser \(q\) und die halbe Grundseite als unser \(p\).

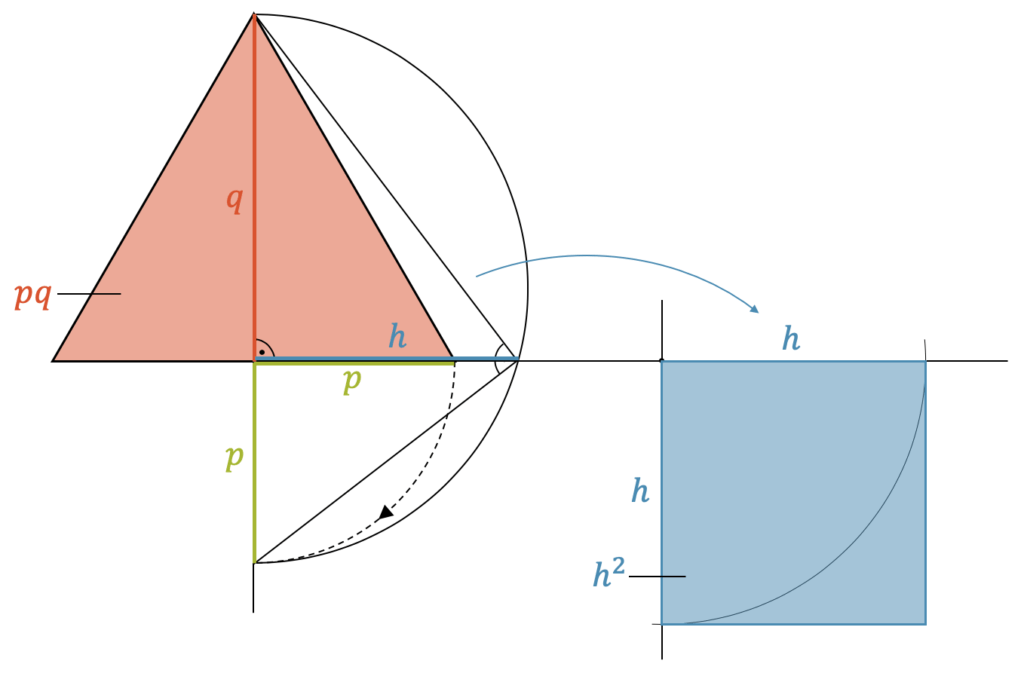
Jetzt nehmen wir die Länge von \(p\) in den Zirkel und tragen sie auf die Verlängerung von \(q\) ein. Wir erhalten so die Grundseite von einem neuen rechtwinkligen Dreieck.

Nun zeichnen wir einen Halbkreis, der als Thaleskreis dienen soll. Wir wissen, dass die gesuchte Höhe die Grundseite in die Teilstücke \(p\) und \(q\) aufteilt. Dort setzen wir an und verlängern so, dass wir einen Schnittpunkt mit dem Thaleskreis erhalten. Die neu erhaltene Höhe ist jetzt so, dass \(h^2\) der Fläche vom Rechteck \(pq\) entspricht. Dieses Rechteck hat ja die Fläche unseres gleichseitigen Dreiecks. Wir brauchen jetzt nur noch mit dem Zirkel die Höhe \(h\) abtragen und schon haben wir das gesuchte Quadrat.

Beispiel

Konstruiere ein Quadrat der Fläche \(12\,\text{cm}^2\).

---

Das Problem ist, dass \(12\) keine Quadratzahl ist, denn sonst könnten wir es sehr einfach konstruieren. Hier brauchen wir aber eine Seitenlänge von \(\sqrt{12}\,\text{cm} = \sqrt{4\cdot3}\,\text{cm} = 2\cdot\sqrt{3}\,\text{cm}\)

Einfacher wäre ein Rechteck, z.B. \(3\,\text{cm} \cdot 4\,\text{cm} = 12\,\text{cm}^2\)

Mit dem Höhensatz können wir sehr einfach ein Rechteck in ein flächengleiches Quadrat umwandeln. Wir zeichnen deshalb eine Dreiecksgrundseite von \(7\,\text{cm}\) und teilen sie auf in \(p = 3\,\text{cm}\) und \(q = 4\,\text{cm}\). Da das Dreieck ein rechtwinkliges Dreieck sein muss, benutzen wir wieder einen Thaleskreis und ziehen die Höhe \(h\) hoch.

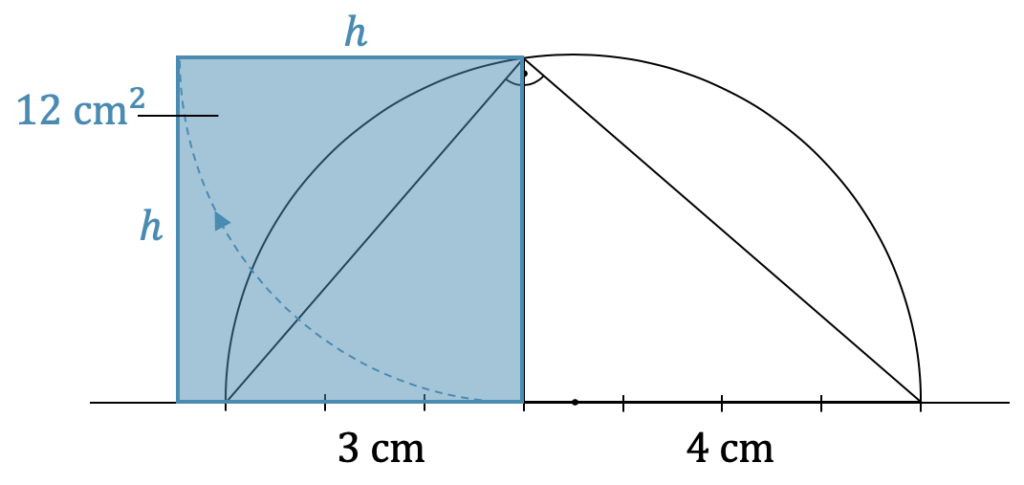
Die so erhaltene Höhe folgt dem Höhensatz, d.h. \(h^2 = pq = 12\,\text{cm}^2\). Wir brauchen jetzt nur noch aus der einen Höhe ein Quadrat zu konstruieren und wir haben genau die Fläche von \(12\,\text{cm}^2\) in quadratischer Form.