Lineare Gleichungssysteme (LGS)

Grundform

Ob wir Spannungen im Material von Brücken, Hochhäusern, in Maschinenteilen, im Flugzeugbau etc. berechnen oder an Klima- und Wettermodellen arbeiten. Wir haben immer mit Gleichungssystemen zu tun.

Was ist ein lineares Gleichungssystem? Ein lineares Gleichungssystem (LGS) besteht aus mehr als einer linearen Gleichung, die alle gleichzeitig erfüllt sein müssen und so ein System bilden. Mit der geschweiften Klammer wird angedeutet, dass die beiden Gleichungen zusammen ein System bilden, z.B.

\[ \begin{cases} \begin{array}{rcrcr} x & + & 2y & = & -1 \quad (1) \\ x & – & y & = & 2 \quad (2) \\ \end{array} \end{cases} \]

Die Lösung dieses Gleichungssystems wäre: \(x=1\) und \(y=-1\), denn nur wenn \(x\) und \(y\) genau diese Werte annimmt, sind beide Gleichungen erfüllt.

Die Gleichungsnummer in Klammern (nach der Gleichung) ist fakultativ und dient einer einfacheren Referenz. Sie wird vor allem beim Additionsverfahren nach Gauss nützlich sein.

Hier werden nur lineare Gleichungssysteme besprochen, d.h. die lineare Gleichung mit den Potenzen \(x^1\), \(y^1\) etc. enthalten, aber keine höheren Potenzen oder andere Funktionen.

Das nachfolgende Beispiel wäre ein nicht-lineares Gleichungssystem, weil die Potenzen der Unbekannten nicht immer 1 sind:

\[ \begin{cases} \begin{array}{cc} 2x + 3 \underline{\sqrt{y}} \;\; = \;\; 1 \\ \underline{-x^2} – y \;\; = \;\; \sqrt{3} \\ \end{array} \end{cases} \]

Die Grundform für ein allgemeines lineares Gleichungssystem mit zwei Unbekannten sieht wie folgt aus:

\[ \begin{cases} \begin{array}{cc} a_1 x + b_1 y = d_1 \quad (1) \\ a_2 x + b_2 y = d_2 \quad (2) \\ \end{array} \end{cases} \]

Allgemeines lineares Gleichungssystem mit drei Unbekannten:

\[ \begin{cases} \begin{array}{cc} a_1 x + b_1 y + c_1 z = d_1 \quad (1) \\ a_2 x + b_2 y + c_2 z = d_2 \quad (2) \\ a_3 x + b_3 y + c_3 z = d_3 \quad (3) \\ \end{array} \end{cases} \]

Lineare Gleichungssysteme können beliebig gross sein. Beachte, dass bei \(n\) Unbekannten und \(n\) Gleichungen, wir eine grosse Anzahl von \(n^2\) Koeffizienten auf der linken Seite der Gleichung haben werden. Der Rechenaufwand nimmt mit der Grösse des Gleichungssystems rasch zu. ????

Gleichungssysteme lösen

Für die Lösung von linearen Gleichungssystemen gibt es verschiedene Verfahren:

• Lösen durch Gleichsetzen
• Lösen durch Einsetzen
• Lösen mit dem Additionsverfahren nach Gauss

Einfache, übersichtliche Gleichungssysteme können mit Gleichsetzen oder Einsetzen schnell und unkompliziert gelöst werden.

Bei weniger einfachen linearen Gleichungssystemen, sicher ab 3 Gleichungen, ist das Additionsverfahren nach Gauss empfohlen, weil wir so mehr Überblick bewahren und unnötige Rechenfehler vermeiden können. ????

Graphische Darstellung eines Gleichungssystems

Zur Veranschaulichung hatten wir die folgende super-einfache Gleichung mit der graphischen Methode gelöst:

\[ x + 1 = 4 \]

Aus dieser einen Gleichung haben wir zwei lineare Gleichungen aufgestellt und in einem \(x,y\)-Diagramm dargestellt. Eine für die linke Seite und eine Zweite für die rechte Seite. Wir schreiben beide Gleichungen schon mal als Gleichungssystem:

\[ \begin{cases} \begin{array}{rcrr} y & = & x + 1 & \quad (1) \\ y & = & 4 & \quad (2) \\ \end{array} \end{cases} \]

Wenn wir die beiden Gleichungen etwas umstellen, so dass auf der linken Seite die Unbekannten sind und auf der rechten Seite nur Zahlen, erhalten wir die Grundform des linearen Gleichungssystems.

\[ \begin{cases} \begin{array}{rcrr} x – y & = & -1 & \quad (1) \\ y & = & 4 & \quad (2) \\ \end{array} \end{cases} \]

Im zweidimensionalen Koordinatensystem bildet jede Gleichung eine Gerade. ????

In unserem Fall schneiden sich die beiden Geraden in einem Schnittpunkt \(A\). Er entspricht dabei der gemeinsamen Lösung, denn er steht für ein bestimmtes Koordinatenpaar \((x,y) = (3,4)\), das beide Gleichungen gleichzeitig erfüllt.

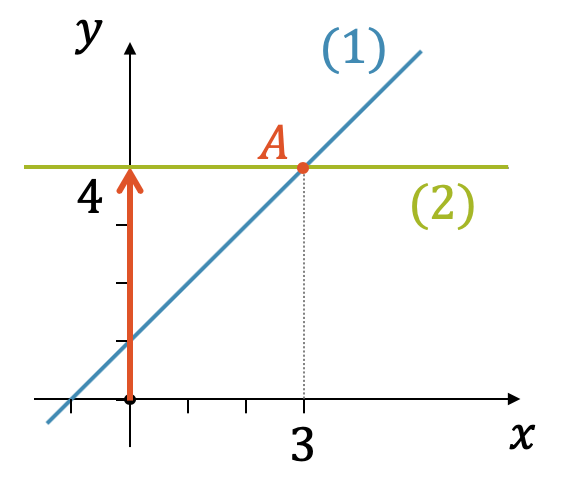
Die Kombination von zwei Zahlenwerten nennen wir ein sog. “2-Tupel”. Die Lösungsmenge des Gleichungssystems enthält eine Lösung, die ein 2-Tupel ist:

\[ \boldsymbol{L} = \Bigl \{ (3,4) \Bigr \} \]

Dreidimensionales lineares Gleichungssystem

Aufbauend auf dem vorigen Beispiel können wir leicht ein Gleichungssystem mit drei Unbekannten aufstellen. Wir fügen eine weitere Gleichung hinzu, beispielsweise:

\[ z = -y + 5 \quad (3) \]

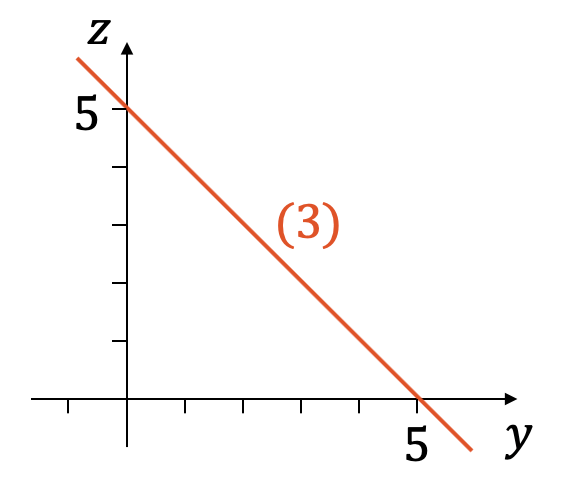
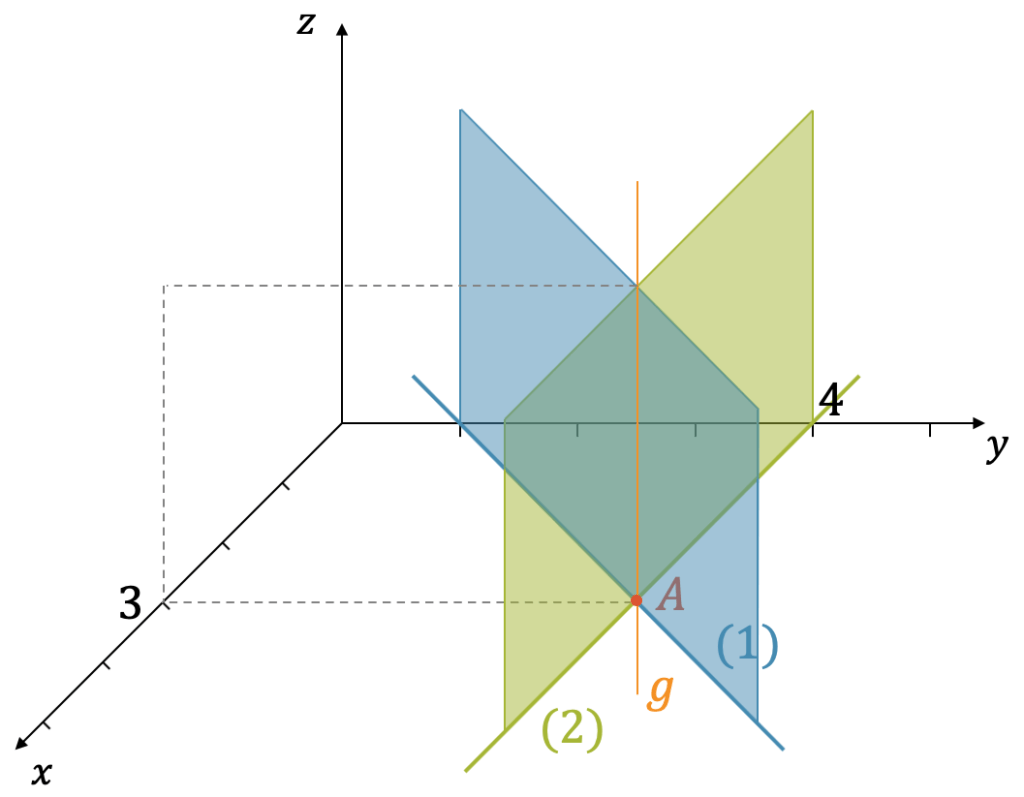
Damit erhalten wir das folgende lineare Gleichungssystem in Grundform:

\[ \begin{cases} \begin{array}{rrrcrr} x & – y & & = &-1 & \quad (1) \\ & y & & = & 4 & \quad (2) \\ & y & + z & = & 5 & \quad (3) \\ \end{array} \end{cases} \]

Beachte: Die ersten beiden Gleichungen machen keine Aussage über \(z\), d.h. sie sind für jeden Wert von \(z\) erfüllt.

Im dreidimensionalen Koordinatensystem entspricht eine lineare Gleichung einer Ebene. ????

Aus unserem Punkt \(A\) wird eine Gerade \(g\): Wir halten die \(x\)- und die \(y\)-Koordinaten fest. Hinzu kommt aber die \(z\)-Koordinate, die frei wählbar ist.

Die Gerade \(g\), die durch \(A\) geht und parallel zur \(z\)-Achse liegt, entspricht der Schnittmenge der beiden Ebenen, wenn wir die gleichzeitige Erfüllung beider Gleichungen (1) und (2) verlangen.

In der folgenden Grafik sind die Ebenen (1) und (2) und die Schnittgerade \(g\) gezeichnet. Aus darstellungstechnischen Gründen sind die Ebenen nicht unendlich gross dargestellt, obwohl sie das natürlich sind.

In gleicher Art können wir auch die neue Gleichung (3) für verschiedene \(x\)-Werte anschauen. \(x\) hat keinerlei Bedeutung für diese Gleichung, d.h. aus der roten Geraden wird eine Ebene für alle beliebigen \(x\)-Werte.

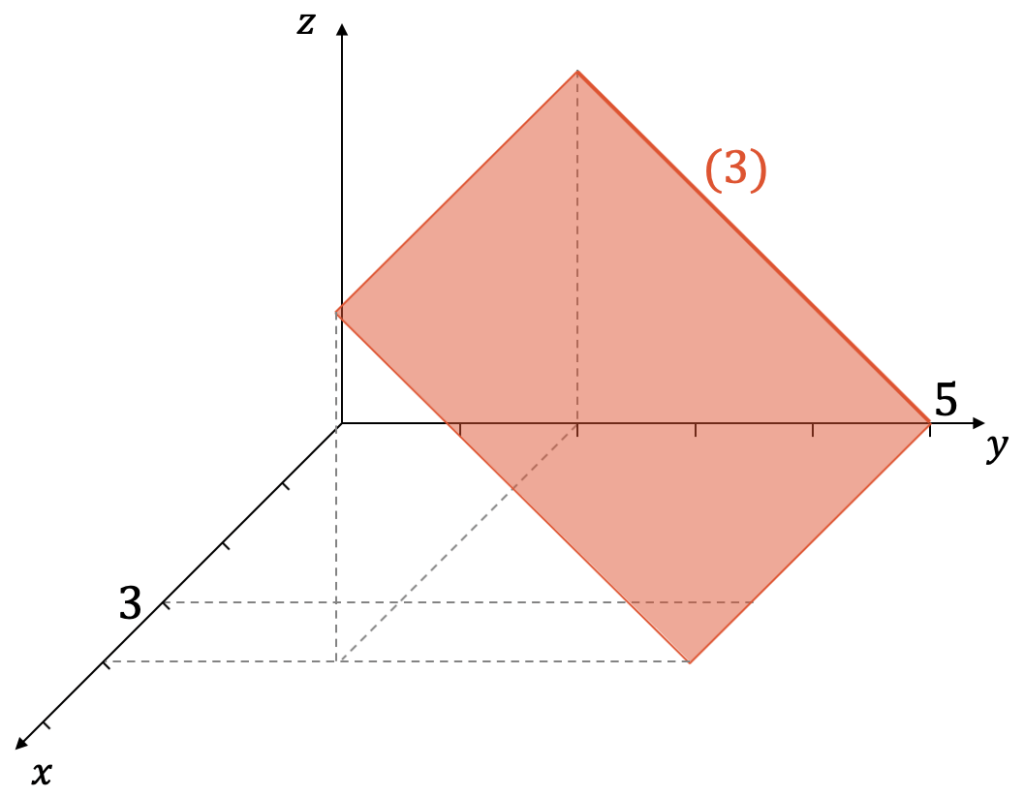
Jetzt verlangen wir, dass alle drei Gleichungen gleichzeitig erfüllt sind, d.h. wir suchen nach der Schnittmenge der drei Ebenen.

Darstellungstechnisch wird das sehr schwierig. Wir können aber die Schnittmenge der ersten beiden Ebenen (1) und (2) als die Gerade \(g\) übernehmen. Wir müssen nur noch die Schnittmenge von \(g\) mit der Ebene (3) finden. Auf diese Weise finden wir den Schnittpunkt \(P\).

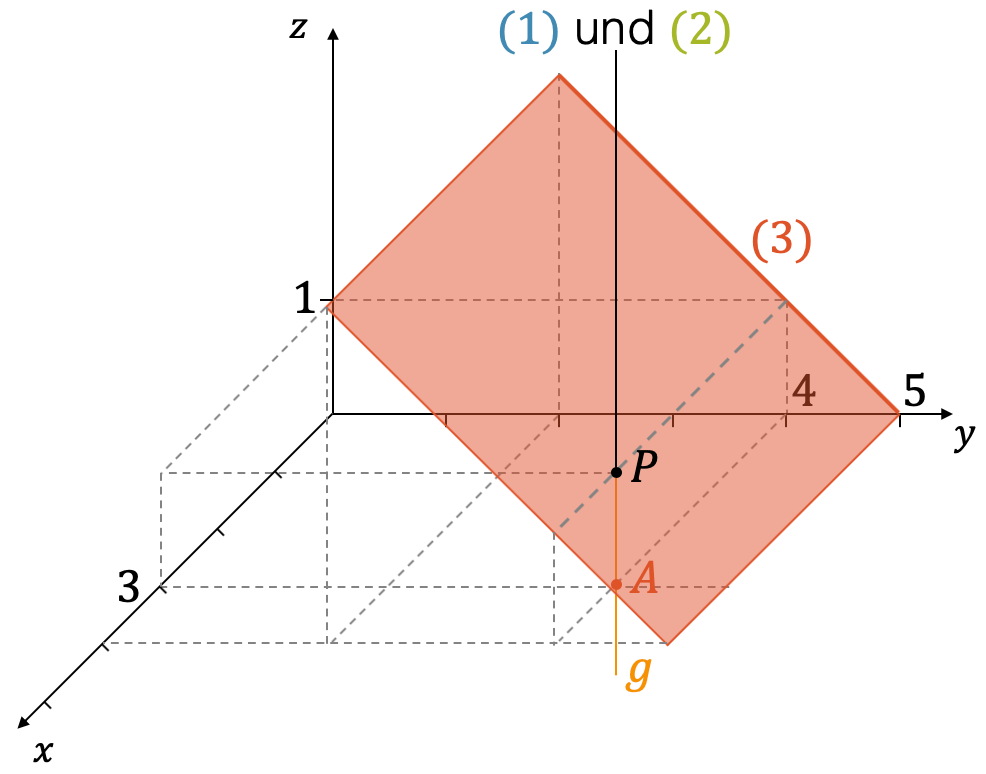
Der Schnittpunkt \(P\) entspricht der Schnittmenge der drei Gleichungen und damit der logischen UND-Verknüpfung der drei Gleichungen:

\[ P \;\;=\;\; (1) \cap (2) \cap (3) \;\;=\;\; g \cap (3) \]

Die Koordinaten von \(P\) geben uns die Zahlenwerte von \(x\), \(y\) und \(z\) und damit das 3-Tupel, das die Lösung des linearen Gleichungssystems ist:

\[ \boldsymbol{L} = \Bigl \{ (3,4,1) \Bigr \} \]

Wir können die Richtigkeit dieser Lösung durch Einsetzen in alle Gleichungen überprüfen: Alle Gleichungen sind erfüllt. ????

Dimension der Lösungsmenge

In den beiden obigen Beispielen haben wir jeweils einen Punkt erhalten als die Lösung des Gleichungssystems.

Damit ein Gleichungssystem lösbar ist, braucht es die gleiche Anzahl Gleichungen, wie die Anzahl Unbekannte, die wir bestimmen sollen. Wir verallgemeinern diese Aussage mit einer einer kleinen Gleichung:

\[ l = u – g \]

Dabei sind:

• Anzahl Unbekannte: \(u\)
• Anzahl Gleichungen: \(g\)

Das Resultat der Differenz ist die Dimension der Lösung \(l\).

Wenn wir genau gleich viele Gleichungen \(g\), wie Unbekannte \(u\) haben, dann ist \(l=0\): Die Lösung ist null-dimensional, d.h. es handelt sich um einen Lösungspunkt (wie oben).

Wenn wir nur die beiden Gleichungen (1) und (2) anschauen (Lösung \(P\)), diese aber im 3-dimensionalen Raum betrachten, d.h. drei Unbekannte haben, nämlich \(x\), \(y\) und \(z\), dann haben wir für (1) und (2) je eine Ebene und der Schnittpunkt von zwei Ebenen ist eine Gerade, d.h. eine eindimensionale Lösungsmenge \(l=1\).

Mit einer dritten Gleichung haben wir eine dritte Ebene. Drei allgemeine Ebenen zusammen schneiden sich in einem Punkt (siehe Abbildung).

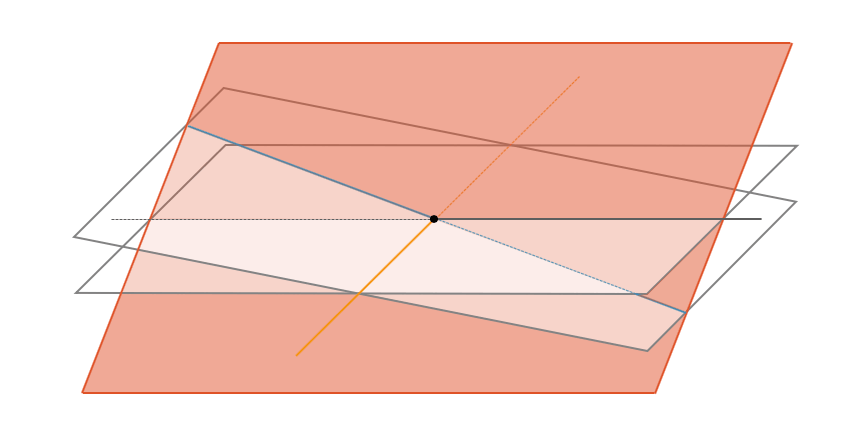
Soweit haben wir den allgemeinen Fall:

• 3 Unbekannte (\(x\), \(y\) und \(z\))
• 3 Gleichungen im Gleichungssystem
• Dimension der Lösung: \(l=u-g=3-3=0\): null-dimensional, d.h. ein Lösungspunkt

Jetzt gibt es aber Spezialfälle, die nicht zu einem Lösungspunkt führen. Wenn die dritte Ebene (rot) parallel zu einer der anderen Ebenen ist, werden wir keinen Lösungspunkt haben:

\[ \boldsymbol{L} = \big\{ \big\} \]

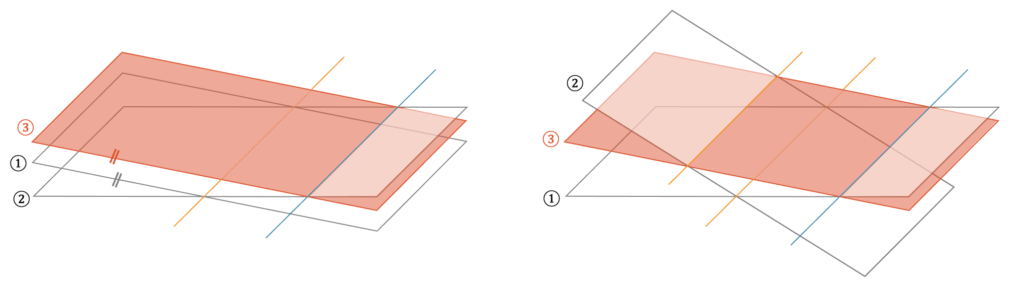
Bei Gleichungssystemen erhalten wir diese oder ähnliche Situationen bei sog. überbestimmten Gleichungssystemen.

Zwei unabhängige Gleichungen sind für zwei Unbekannte genug. Wenn wir aber drei Gleichungen haben für zwei Unbekannte, dann muss die dritte Gleichung mit der Lösung aus den ersten beiden Gleichungen ebenfalls erfüllt sein. Ist sie das nicht, haben wir die Situation in der oben Grafik rechts.

Liegt die dritte Ebene aber so, dass die gemeinsame Gerade der ersten beiden Ebenen sogar in der dritten Ebene liegt, erfüllt die ganze Punktschar der Geraden die Bedingung, alle drei Gleichungen zu erfüllen. Die Gerade liegt dann ja in allen drei Ebenen gleichzeitig und somit erfüllen alle Punkte der Geraden die drei Gleichungen gleichzeitig. Wir haben in diesem Fall unendlich viele Lösungspunkte

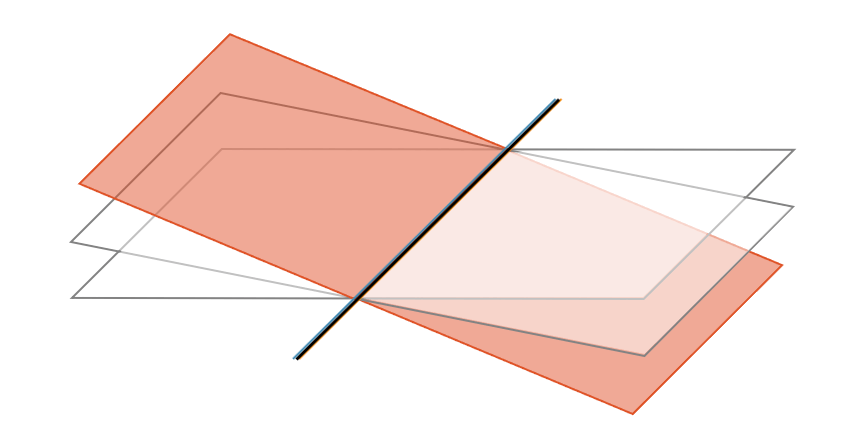
Dieses Prinzip gilt auch bei höheren Dimensionen, jedoch können wir uns das nicht mehr bildlich vorstellen.

Es gibt aber eine rein algebraische Methode mit Hilfe der sog. Determinante \(\det(A)\), mit welcher wir herausfinden können, ob unser lineares Gleichungssystem genau eine Lösung hat, oder keine bzw. \(\infty\)-lich viele Lösungen.

Determinante bestimmen und auswerten

Aus den Koeffizienten des linearen Gleichungssystems wird in einem ersten Zwischenschritt die Matrix \(A\) aufgestellt und für diese dann eine Determinante \(\det(A)\) berechnet. Sie ist eine Zahl mit den folgenden Bedeutungen:

• \(\det(A) \neq 0 \qquad \Leftrightarrow \qquad\) Das Gleichungssystem hat genau eine Lösung (Punktlösung)
• \(\det(A) = 0 \qquad \Leftrightarrow \qquad\) Das Gleichungssystem hat keine oder unendlich viele Lösungen.

Beachte, dass eine verschwindende Determinante die beiden Fälle (keine/\)\infty\)) nicht unterscheiden kann, denn das entscheiden die Koeffizienten auf der rechten Seite des Gleichungssystems, die nicht in \(A\) eingeflossen sind.

Andersrum: Eine verschwindende Determinante bedeutet, dass es mindestens zwei Gleichungen gibt, die ein Vielfaches von einander sind, d.h. diese Gleichungen sind Doppelgänger und sollten eigentlich nur als eine Gleichung gezählt werden. ????

So wird die Determinante berechnet:

\[ \begin{cases} \begin{array}{cc} a_1 x + b_1 y = d_1 \\ a_2 x + b_2 y = d_2 \\ \end{array} \end{cases} \qquad \rightarrow \qquad A = \begin{pmatrix} a_1 \;\; b_1 \\ a_2 \;\; b_2 \end{pmatrix} \]

\[ \det(A) = a_1 \cdot b_2 – a_2 \cdot b_1 \]

Die Berechnung der Determinante einer 3×3-Matrix ist etwas umfangreicher:

\[ A = \begin{pmatrix} a_1 \;\; b_1 \;\; c_1 \\ a_2 \;\; b_2 \;\; c_2 \\ a_3 \;\; b_3 \;\; c_3 \\ \end{pmatrix} \]

\[ \det(A) = a_1 \cdot (b_2 \cdot c_3 – c_2 \cdot b_3) – b_1 \cdot (a_2 \cdot c_3 – c_2 \cdot a_3) + c_1 \cdot (a_2 \cdot b_3 – b_2 \cdot a_3) \]

Determinanten können auch für grössere Matrizen berechnet werden, jedoch wird die Rechnung immer länger.

Wie wir mit einem Problem umgehen müssen, das keine oder unendlich viele Lösungen hat, siehst du in folgendem Beispiel: