Das Wichtigste in Kürze
Das dreidimensionale Koordinatensystem wird meistens wie folgt gezeichnet:
-
-
- \((x,y)\)-Ebene liegt gedreht vor uns
- Die Zeichenebene ist neu die \((y,z)\)-Ebene
- Die \(z\)-Achse übernimmt die Rolle der “Höhe”
- Die \(x\)-Achse zeigt perspektivisch aus der Zeichenebene heraus (Parallelperspektive mit 45°-Winkel, verkürzte Skala)
-
Punkte können eindeutig eingezeichnet werden, jedoch kann von einem Punkt nicht mehr eindeutig bestimmt werden, welche Koordinaten er hat.
Videos
-
Dreidimensionales-Koordinatensystem (Tutorial)
Dauer: 7 min 10 s
Für die räumliche Vektorgeometrie brauchen wir eine Möglichkeit, Vektoren, Geraden, Punkte usw. im Raum darzustellen. Dazu benutzen wir ein Koordinatensystem mit den drei Dimensionen \(x\), \(y\) und \(z\). Es ist üblich dafür die Parallelperspektive zu verwenden. Die Zentralperspektive würde zwar besser aussehen, wäre aber viel zu aufwendig. Auf der \(x\)-Achse werden die Abstände auf der Skala etwas verkürzt im Vergleich zu den Abständen auf der \(y\)- und \(z\)-Achse.
Die \(y\)- und die \(z\)-Koordinaten legen wir neu in die Zeichenebene. Das ist am Anfang etwas gewöhnungsbedürftig, denn hier sind wir gewohnt die \(x\)- und die \(y\)-Koordinate zu haben. Vor allem zeigt die \(y\)-Achse jetzt plötzlich horizontal nach rechts!
Die \(x\)-Koordinate haben wir nach vorne gelegt, also eigentlich räumlich aus der Zeichenebene heraus. Für die perspektivische Darstellung nehmen wir einen 45°-Winkel, weil der am einfachsten ist. Wir sehen jetzt, dass die \((x,y)\)-Ebene unten liegt (grün eingefärbt). Wir schauen irgendwie von oben darauf.
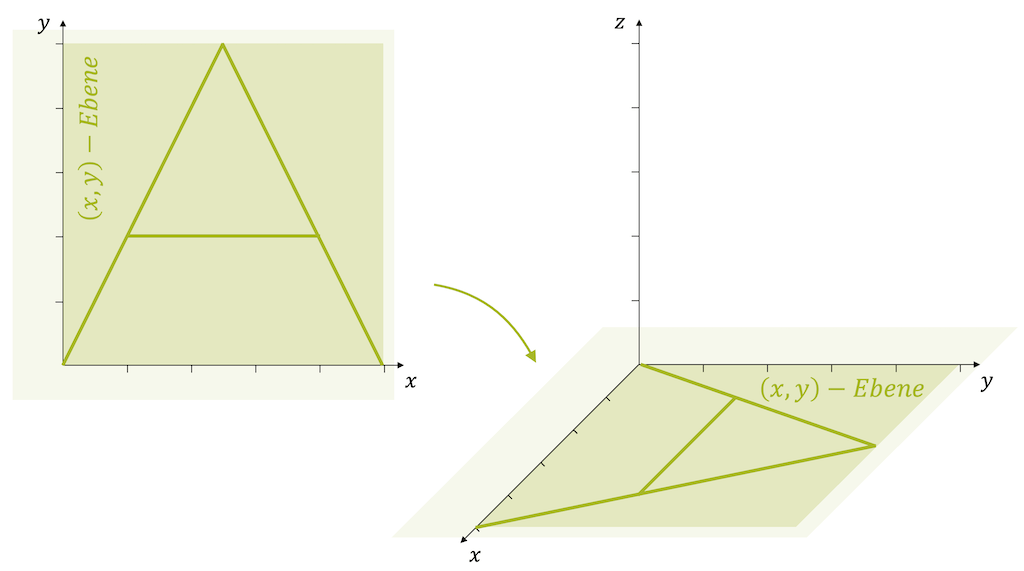
Das dreidimensionale Koordinatensystem wird meistens wie folgt gezeichnet:
- \((x,y)\)-Ebene liegt gedreht vor uns
- Die Zeichenebene ist neu die \((y,z)\)-Ebene
- Die \(z\)-Achse übernimmt die Rolle der “Höhe”
- Die \(x\)-Achse zeigt perspektivisch aus der Zeichenebene heraus (Parallelperspektive mit 45°-Winkel, verkürzte Skala)
Punkte können eindeutig eingezeichnet werden, jedoch kann von einem Punkt nicht mehr eindeutig bestimmt werden, welche Koordinaten er hat.
Beispiel
Zeichne die folgenden vier Punkte in ein dreidimensionales Koordinatensystem ein.
\[ A(2,-3,4), \quad B(3,2,-1), \quad C(-4-2,0) \quad D(0,0,2) \]
Zeichne anschliessend die Vektoren \(\overrightarrow{OA}\) und \(\overrightarrow{CD}\).
Die Lösung ist in der folgenden Grafik dargestellt. Für den Punkt \(A\) gehen wir vom Ursprung zuerst zwei Schritte in \(x\)-Richtung, d.h. zwei Schritte aus der Zeichenebene heraus, nach vorne. Dann gehen wir 3 Schritte nach links, d.h. der \(y\)-Achse entgegengesetzt. Schliesslich gehen wir die 4 Schritte nach oben (\(z\)-Richtung). Mit den Hilfslinien erkennen wir so etwas wie einen stehenden Quader, der uns bei der dreidimensionalen Vorstellung hilft.
Für den Punkt \(B\) haben wir die Hilfslinien absolut minimal gehalten. Wir gehen 3 Schritte in Richtung der \(x\)-Achse, d.h. 3 Schritte nach vorne (schräg nach unten). Dann geht es zwei Schritte nach rechts (\(y\)-Richtung) und einen nach unten (\(z\)-Richtung). Der Punkt \(B\) liegt gewissermassen im ersten Kellergeschoss unterhalb des Punkts \((3,2,0)\).
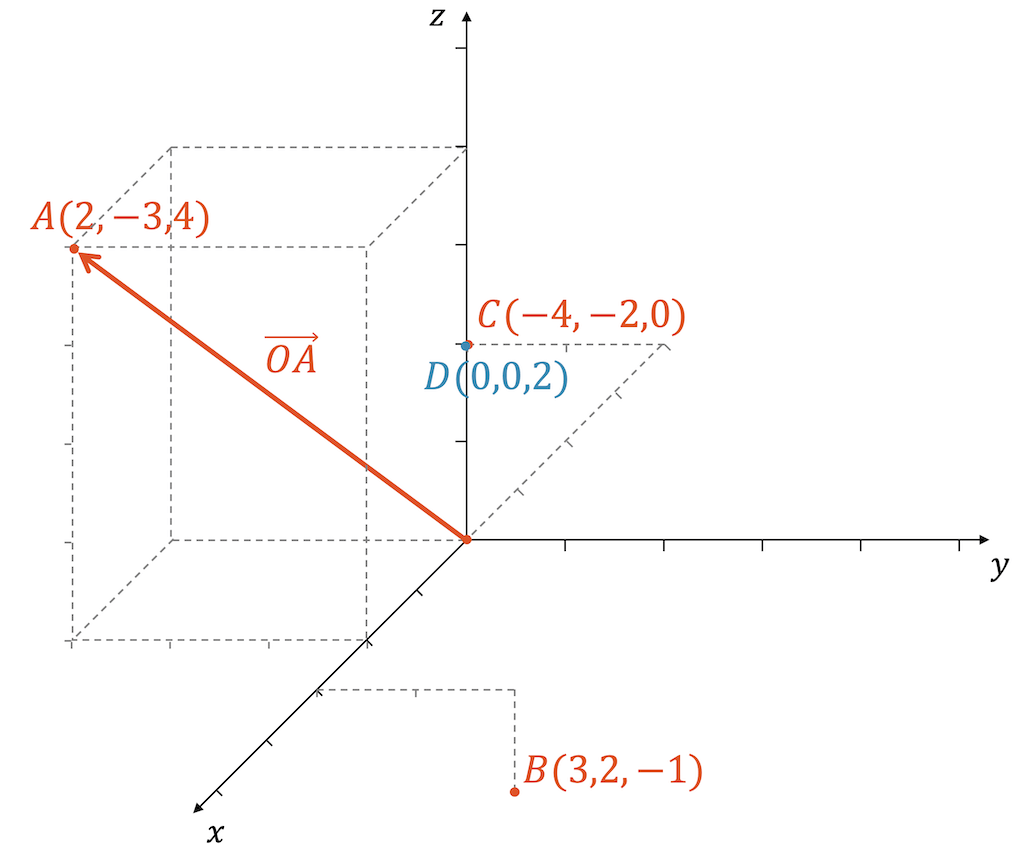
Der Punkt \(C\) ist noch von besonderem Interesse. Wir sehen, dass er mit dem Punkt \(D\) zusammenfällt. Das liegt aber nur an der perspektivischen Darstellung, denn die Koordinaten der beiden Punkte sind total verschieden:
\[ C(-4,-2,0) \quad \neq \quad D(0,0,2) \]
Der Punkt \(C\) liegt in der \((x,y)\)-Ebene. Er liegt dummerweise aber auch noch genau hinter der \(z\)-Achse, auf welcher der Punkt \(D\) liegt. Das ist eine der Schwächen des dreidimensionalen Koordinatensystems: Wir können zwar Punkte eindeutig einzeichnen. Wenn wir aber die Hilfslinien wegnehmen, können wir von einem Punkt unmöglich die Koordinaten ablesen. Da wir viele Punkte haben, die genau hintereinander liegen.
Mit den Vektoren ist das ähnlich: Der Ortsvektor von \(A\) (\(\overrightarrow{OA}\)) kann sehr gut dargestellt werden. Hingegen erscheint der Vektor \(\overrightarrow{CD}\) nur noch als Punkt, weil schon die beiden Punkte \(C\) und \(D\) hintereinander liegen. Wir können in dieser Darstellung nicht alles perfekt zeichnen und müssten im Notfall das Koordinatensystem drehen.
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.