Inhalt
Das Wichtigste in Kürze
Der Carnot-Wirkungsgrad \(\eta_C\) ist der physikalisch best-mögliche Wirkungsgrad einer idealen Wärmekraftmaschine (WKM). Reale Wärmekraftmaschinen erreichen max. etwa 2/3 von\(\eta_C\), da alle realen Prozesse mit Verlusten (z.B. Reibung) behaftet sind.
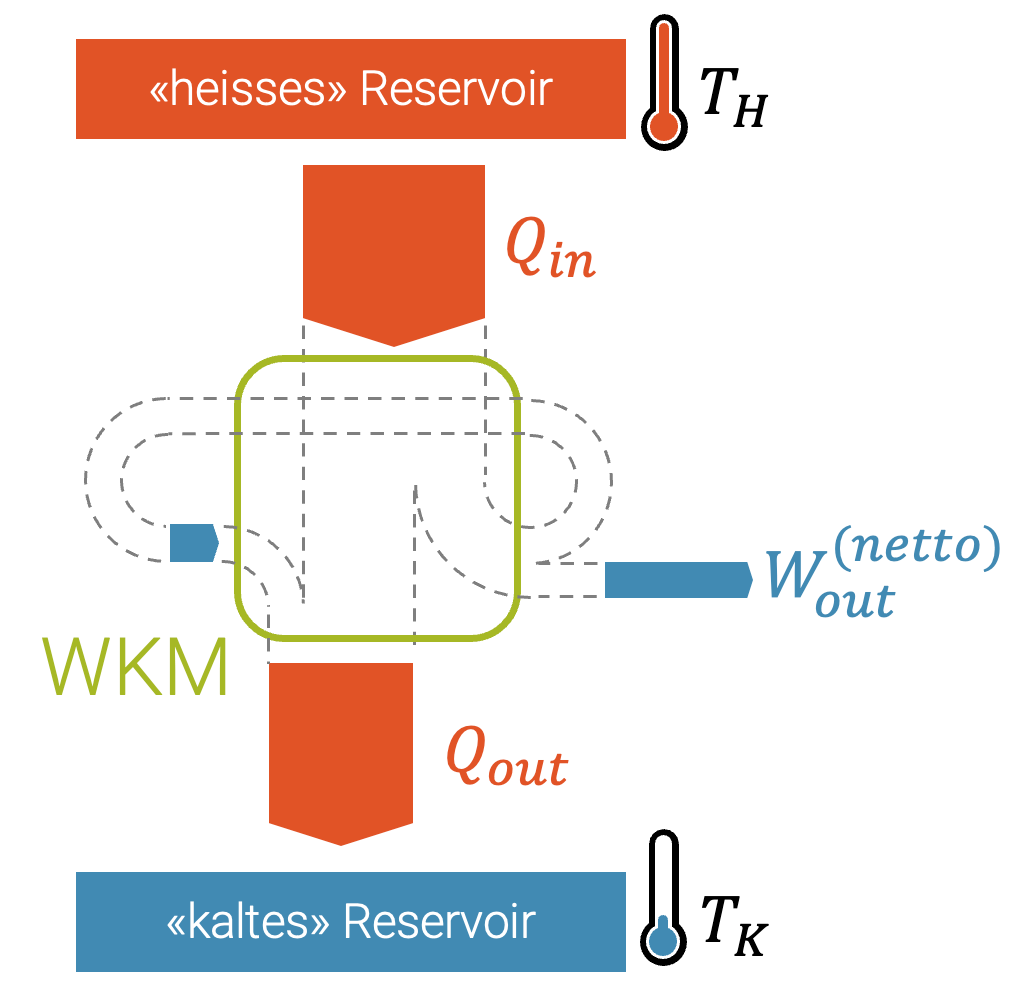
Der Carnot-Wirkungsgrad wird aufgrund der Temperaturen der beiden Wärme-Reservoirs der WKM berechnet: Die hohe Temperatur \(T_H\), bei welcher Wärme aufgenommen wird und die tiefe Temperatur \(T_K\), bei welcher die Abwärme abgegeben wird.
\[ \eta_C = 1 – \frac{T_K}{T_H} \]
Beachte, dass für \(T_H\) und \(T_K\) die absoluten Temperaturen in Kelvin eingesetzt werden müssen.
Nicolas Léonard Sadi Carnot (1796 – 1832) war französischer Physiker und Ingenieur. Er gilt als Begründer der Thermodynamik.
Der von ihm gefundene und nach ihm benannte Carnot-Wirkungsgrad ist der ideale Wirkungsgrad, den eine Wärmekraftmaschine (WKM) im theoretisch idealsten Fall erreichen kann.
Wie wir wissen, herrscht in sämtlichen realen Maschinen immer etwas Reibung, d.h. der Carnot-Wirkungsgrad gilt als theoretische Obergrenze, die real aber gar nicht erreicht werden kann.
Bei gewöhnlichen Maschinen liegt die theoretische Obergrenze für den Wirkungsgrad bei 100%. Maschinen nehmen Energie \(\Delta E_{\text{in}}\) auf und geben sie, meist als mechanische Arbeit \(W_{\text{out}}\) wieder ab.
Da Maschinen über eine längere Zeit einen konstanten Betrieb haben, können wir es ausschliessen, dass ein Energieüberschuss sich irgendwo in der Maschine akkumuliert oder dass die Maschine einen Energiespeicher entleert. Im stationären Betrieb ist die eintretende Energie gleich der aus der Maschine austretende Energie:
\[ \Delta E_{\text{in}} \;\; = \;\; W_{\text{out}} \]
Dies ist begründet durch die Energieerhaltung bzw. durch den Ersten Hauptsatz der Thermodynamik. Daraus folgt:
\[ \eta_{\text{ideal}} = \frac{W_{\text{out}}}{\Delta E_{\text{in}}}= 100\% \]
Für Wärmekraftmaschinen ist diese theoretische Obergrenze nicht durch den Ersten Hauptsatz, sondern durch den Zweiten Hauptsatz der Thermodynamik gegeben und damit deutlich tiefer.
\[ \eta_{\text{ideal}} = \eta_C = 1-\frac{T_K}{T_H} < 100\% \]
Der Zweite Hauptsatz berücksichtigt die Entropie, die von der jeweiligen Temperatur abhängig ist, bei welcher Wärme aufgenommen oder abgegeben wird.
Beispiel
Herleitung
Der Zweite Hauptsatz verbietet, dass Entropie vernichtet wird. Die Wärmekraftmaschine nimmt Entropie auf und erzeugt vielleicht auch Entropie durch irreversible Prozesse im Innern der Maschine (Reibung, Wirbel etc.).
Die Wärmekraftmaschine muss die aufgenommene und die erzeugte Entropie wieder abgeben. Sonst würde die Entropie in der Maschine immer mehr zunehmen.
Im idealsten Fall haben wir keinerlei Reibung, d.h. es entsteht in der Wärmekraftmaschine keine zusätzliche Entropie. In diesem Fall ist die aufgenommene Entropie \(S_{\text{in}}\) gleich der abgegebenen Entropie \(S_{\text{out}}\):
\[ S_{\text{in}} \;\;=\;\; S_{\text{out}} \]
Die abgegebene Arbeit \(W_{\text{out}}\) enthält keine Entropie, d.h. die ganze Entropie fliesst zusammen mit der Wärme, sowohl bei der aufgenommenen Wärme \(Q_{\text{in}}\), wie bei der abgegebenen Abwärme \(Q_{\text{out}}\).
Tatsächlich kommt jeder Wärmestrom immer mit Entropie daher, abhängig davon, bei welcher Temperatur die Wärme ausgetauscht wird.
\[ S_{\text{in}} = \frac{Q_{\text{in}}}{T_H} \]
\[ S_{\text{out}} = \frac{Q_{\text{out}}}{T_K} \]
\[ \frac{Q_{\text{in}}}{T_H} \;\; = \;\; \frac{Q_{\text{out}}}{T_K} \]
Wir erhalten daraus die Beziehung:
\[ \frac{Q_{\text{out}}}{Q_{\text{in}}} \;\; = \;\; \frac{T_K}{T_H} \]
Gemäss Erstem Hauptsatz der Thermodynamik (Energieerhaltung) gilt:
\[ Q_{\text{in}} = W_{\text{out}} + Q_{\text{out}} \]
\[ W_{\text{out}} = Q_{\text{in}} – Q_{\text{out}} \]
Der Carnot-Wirkungsgrad ist definiert als die durch die WKM gewonnene (nützliche) Arbeit \(W_{\text{out}}\) im Vergleich zur eingesetzten Wärme \(Q_{\text{in}}\):
\[ \eta_C = \frac{W_{\text{out}}}{Q_{\text{in}}} \]
Wir ersetzen im Zähler die Arbeit mit dem eben erhaltenen Ausdruck aus der Energieerhaltung:
\[ \eta_C = \frac{Q_{\text{in}} – Q_{\text{out}}}{Q_{\text{in}}} \]
\[ \eta_C = 1 – \frac{Q_{\text{out}}}{Q_{\text{in}}} \]
Jetzt setzen wir den Ausdruck ein, den wir aus \(S_{\text{in}}=S_{\text{out}}\) gefunden hatten und erhalten damit die Formel für die Berechnung des Carnot-Wirkungsgrads:
\[ \eta_C = 1 – \frac{T_K}{T_H} \]
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.