
Beim Hebelgesetz sind meistens zwei Drehmomente im Drehmomentgleichgewicht. Durch die unterschiedlichen Abstände sind die beiden beteiligten Kräfte unterschiedlich gross. Bei vielen Werkzeugen im Alltag (Schere, Zange, Locher, Nussknacker etc.) wird das Hebelgesetz ausgenutzt, um die Kraft des Menschen um ein Vielfaches zu vergrössern. Diese Werkzeuge gehören deshalb auch zu den Kraftwandlern.
Drehmomentgleichgewicht beim Hebel
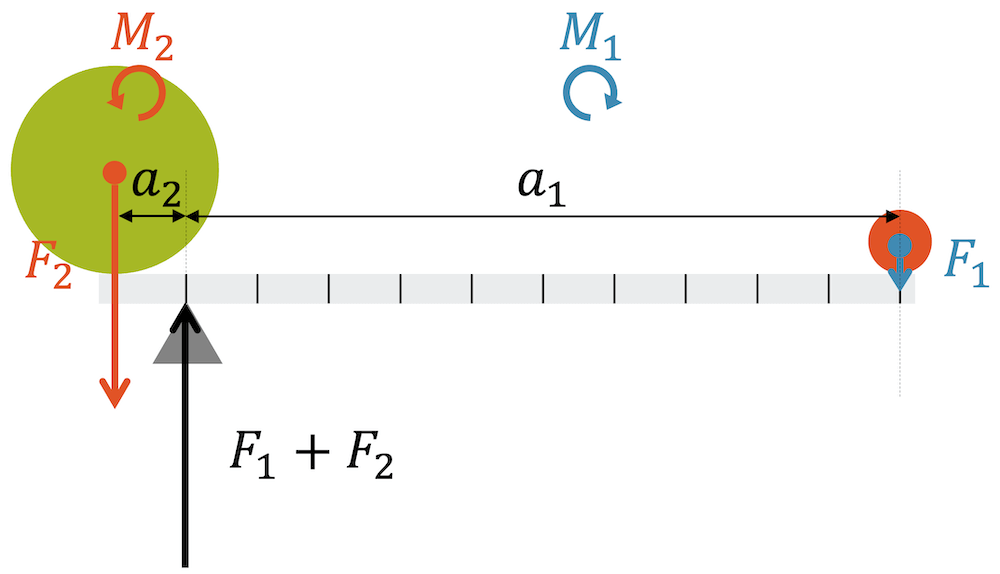
Um das Hebelgesetz zu erklären, schauen wir uns das Beispiel mit den ungleich grossen Kugeln auf einer “Balkenwaage” an. Als Betrachtungspunkt für das Drehmoment nehmen wir den Auflagepunkt. Wir sehen, dass die grosse Kraft \(F_2\) einen kleinen Abstand \(a_2\) zum Auflagepunkt und die kleine Kraft \(F_1\) einen grossen Abstand \(a_1\) haben. Addieren wir die beiden Drehmomente, so erhalten wir das resultierende Drehmoment \(M_{res}\). Im Fall des Drehmomentgleichgewichts wissen wir, dass das resultierende Drehmoment \(M_{res}\) null sein muss:
\[ \vec{M_{res}} = \vec{M_1} + \vec{M_2} = 0 \]
Wir kriegen deshalb:
\[ \vec{M_1} = -\vec{M_2} \]
Die beiden Drehmomente sind im Betrag gleich, haben jedoch eine umgekehrte Richtung. Für den Betrag können wir schreiben:
\[ M_1 = |\vec{M_1}| = |-\vec{M_2}| = M_2 \]
Setzen wir die Definition der Drehmomente \(M_1 = F_1 \cdot a_1\) bzw. \(M_2 = F_2 \cdot a_2\) oben ein, so erhalten wir:
\[ F_1 \cdot a_1 = F_2 \cdot a_2 \]
Jetzt lösen wir nach \(F_2\) auf und erhalten:
\[ F_2 = \frac{a_1}{a_2} \cdot F_1 \]
Das Verhältnis der beiden Abstände \(\frac{a_1}{a_2}\) ergibt den Faktor zwischen den beiden Kräften \(F_1\) und \(F_2\). Wenn wir ein viel grösseres \(a_1\) als \(a_2\) haben, so wird der Faktor gross. In diesem Beispiel ist der Abstand \(a_1\) 10 Einheiten lang und \(a_2\) nur eine Einheit lang. Damit ist \(\frac{a_1}{a_2}=10\) und für die Kräfte folgt \(F_2 = 10 \cdot F_1\), d.h. die Kraft \(F_2\) ist 10-mal grösser als die Kraft \(F_1\).
Mit Hilfe eines sog. Hebels, können wir durch das Verhältnis der beiden Abstände eine Kraft sehr stark vergrössern (oder abschwächen). Man nennt ein System, das aus einer Kraft eine andere um ein Vielfaches vergrösserte oder verkleinerte Kraft erzeugt, einen Kraftwandler.
Alltagsbeispiele
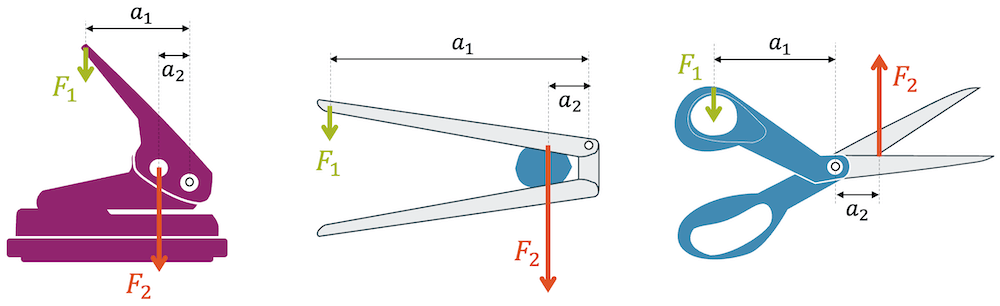
Viele Alltagsgegenstände nutzen das Hebelgesetz aus. Die Handkraft auf den Locher wird über den grossen Abstand \(a_1\) eingeleitet. Das eigentliche Werkzeug, das die Löcher aus dem Papier herausstanzt, steht bewusst im kleinen Abstand \(a_2\) vom Drehpunkt. Das Verhältnis \(\frac{a_1}{a_2}\) der beiden Abstände beträgt in diesem Beispiel etwa 4. Beim Betätigen des Lochers erreichen eine etwa vierfache Kraft auf dem Stanzwerkzeug. Ohne Hebelgesetz müssten wir die vierfache Kraft selber aufbringen!
Baumnüsse sind sehr hart und können nur mit einer grossen Kraft geknackt werden. Wir sehen, dass das Verhältnis \(\frac{a_1}{a_2}\) etwa 7-8 beträgt. Wir können daher unsere Muskelkraft um diesen Faktor vergrössern.
Bei der Schere wird das Hebelgesetz ganz deutlich: Schneiden wir bei stark geöffneter Schere, so schneidet sie besser als an der Spitze, obwohl sie überall gleich scharf geschliffen ist. Mit dem Hebelgesetz haben wir nahe am Drehpunkt einen kurzen Abstand \(a_2\) und damit einen grossen Faktor, der die Kraft \(F_2\) vergrössert. An der Spitze ist der Abstand \(a_2\) etwa gleich gross wie \(a_1\), so dass die Kraft \(F_2\) gegenüber \(F_1\) nicht vergrössert ist.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.