Drehmoment

Das Drehmoment \(M\) ist eine Vektorgrösse, die aus einer Kraft \(F\) und dem senkrechten Abstand \(a\) (Lot) von einem betrachteten Punkt zur Wirkungslinie dieser Kraft, zusammengesetzt ist:

\[ M=F \cdot a \]

Die Drehrichtung des Drehmoments wird im Uhrzeiger- bzw. Gegenuhrzeigersinn angegeben oder mit Hilfe der Rechten-Hand-Regel als einen geraden Vektor angegeben, der in der Drehachse liegt.

Mit Hilfe des Drehmoments kann das Kräftegleichgewicht mit dem Drehmomentgleichgewicht ergänzt werden, so dass mechanische Systeme in der Statik (z.B. Gebäude, Brücken, Türme etc.) korrekt berechnet werden können. Insbesondere werden damit die Kräfte erklärt, die das System auffangen muss, damit es weiterhin stabil bleibt.

Aus dem Drehmomentgleichgewicht folgt auch das Hebelgesetz, welches uns erlaubt Kräfte von Alltagsgegenständen zu vergrössern. Schliesslich folgt auch die Eigenschaft des Schwerpunkts aus dem Drehmomentgleichgewicht.

Definitionen

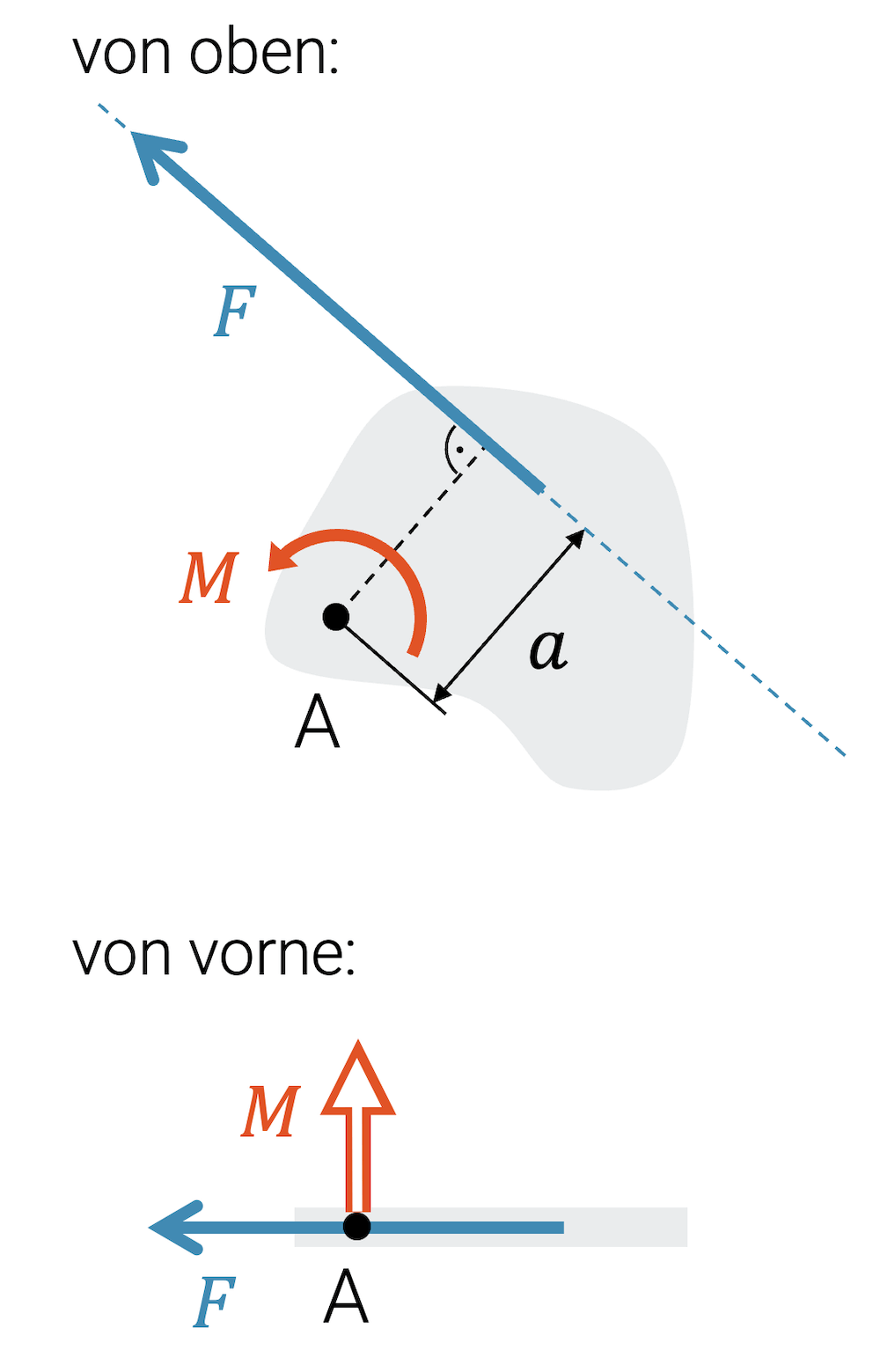
Abkürzung: \(\vec{M}\)

Einheiten: \([\,|\vec{M}|\,] = \mathrm{Nm}\)

Beachte, dass die Einheit \(\mathrm{Nm}\) üblicherweise nicht in \(\mathrm{J}\) (Joule) umgeschrieben wird.

Das Drehmoment \(M\) ist ein Produkt einer Kraft \(F\) und dem senkrechten Abstand \(a\) von einem Punkt zu der Wirkungslinie dieser Kraft. Somit ist das Drehmoment nicht nur abhängig von der Kraft, sondern auch vom betrachteten Punkt und v.a. vom Abstand zur Wirkungslinie der Kraft:

\[ M=F \cdot a \]

Die Richtung des Drehmoments wird in zweidimensionalen Problemen mit einem Drehpfeil gezeichnet oder mit Uhrzeigersinn bzw. Gegenuhrzeigersinn beschrieben, wobei der Drehsinn sich auf die Zeichnung bezieht. Betrachtet man eine Drehung, die nicht mit einem Drehpfeil gezeichnet werden kann, so zeigt ein gerader Pfeil mit doppelter Linie die Drehachse. Mit der Rechte-Hand-Regel können wir den Daumen in die Richtung dieses “Doppelpfeils” legen und an den anderen, leicht gekrümmten Fingern die Drehrichtung erkennen.

Beispiel 

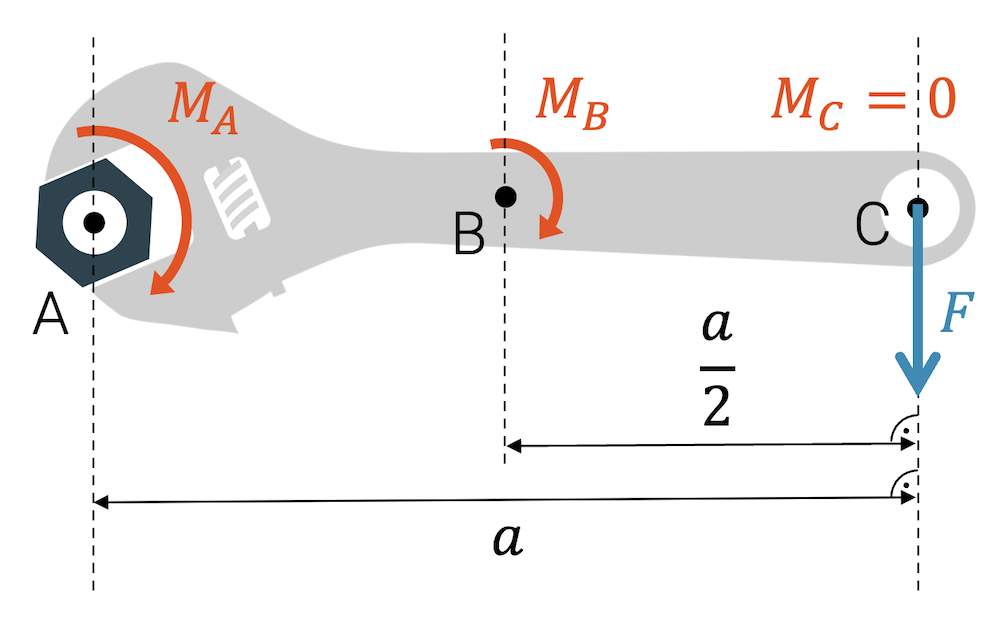
Die Kraft \(F\) beträgt 100 N und wirkt auf das rechte Ende des Gabelschlüssels. Der Abstand \(a\) beträgt 20 cm.

Wie gross sind die Drehmomente in den Punkten A, B und C?

Im Punkt A haben wir einen senkrechten Abstand zur Wirkungslinie der Kraft \(F\) von \(a\). Somit gilt für das Drehmoment:

\[ M_A=F \cdot a = 100\,\mathrm{N} \cdot 0.2\,\mathrm{m} = 20\,\mathrm{Nm}  \]

Für den Punkt B haben wir die gleiche Kraft, jedoch nur den halben Abstand \(\frac{a}{2}\). So erhalten wir:

\[ M_B=F \cdot \frac{a}{2} = 100\,\mathrm{N} \cdot 0.1\,\mathrm{m} = 10\,\mathrm{Nm}  \]

Im Punkt C verschwindet der Abstand zur Wirkungslinie der Kraft, da der Punkt C direkt auf ihr liegt. Das ist aber auch dann der Fall, wenn der Kraftvektor und der Punkt C sich nicht direkt berühren, C aber auf der Wirkungslinie, d.h. der Verlängerung der Kraft liegt.

\[ M_C = 0 \]

Beispiel 

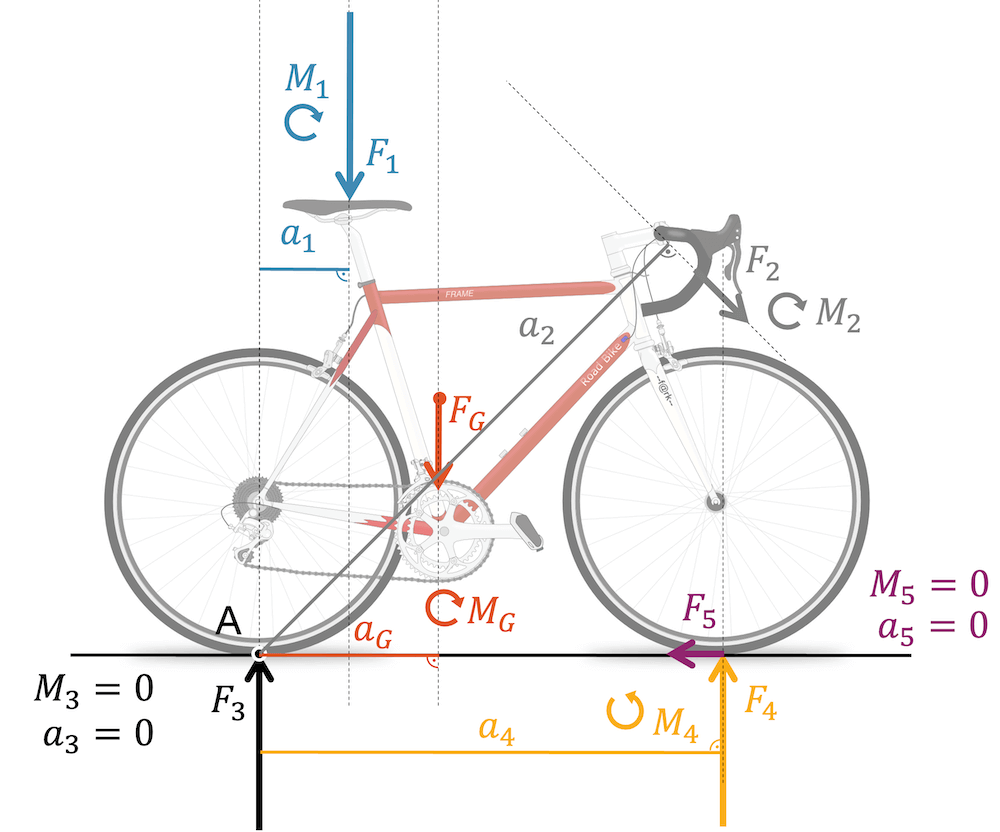
An einem Rennrad wirken verschiedene Kräfte. Der zu betrachtende Punkt A wurde in diesem Beispiel unter das Hinterrad gesetzt. Die für die Drehmomente wesentlichen Abstände werde durch ein Lot auf die Wirkungslinie der Kraft ermittelt.

Die Kraft \(F_1\) wirkt auf den Sattel. Die Wirkungslinie, die durch \(F_1\) geht, ist eine Vertikale, die rechts vom betrachteten Punkt A in den Boden verläuft. Der Abstand zu A ist in der Zeichnung mit \(a_1\) eingezeichnet. Nun könnten wir das Drehmoment mit \(M_1 = F_1 \cdot a_1\) berechnen. Für die Drehrichtung von \(M_1\) stellen wir uns vor, dass wir im Punkt A sitzen und der Kraftpfeil \(F_1\) wie eine kleine Eisenbahn auf ihrer Wirkungslinie vor uns von oben nach unten vorbeifährt. Diese imaginäre Bewegung gibt uns die Drehrichtung.

Die Kraft \(F_2\) wirkt am Lenker. Ihre Wirkungslinie verläuft von oben links in der Zeichnung, nach unten rechts. Das Lot auf die Wirkungslinie der Kraft hat den Betrag \(a_2\) und schneidet die Wirkungslinie beim Lenker selbst. Obwohl die Kraft \(F_2\) nicht sonderlich gross ist, wird das Drehmoment \(M_2\) aufgrund des grossen Abstands \(a_2\) vermutlich grösser ausfallen, als \(M_1\).

Die Kraft \(F_3\) wirkt direkt auf den Punkt A. Damit ist auch klar, dass der Abstand zur Wirkungslinie \(a_3 = 0\) sein muss und wir deshalb kein Drehmoment \(M_3\) haben.

Am untersten Punkt des Vorderrads wirkt die Kraft \(F_4\) in einem Abstand \(a_4\) zum Punkt A.

Die Kraft \(F_5\) hat eine Wirkungslinie, die durch den Punkt A geht und somit haben wir auch für diese Kraft keinen Abstand \(a_5\) und somit gilt auch: \(M_5=0\).

Die Gewichtskraft \(F_G\) wirkt am Schwerpunkt des Fahrrads. Ihre Wirkungslinie verläuft, wie diejenige von \(F_1\) von oben nach unten, jedoch in einem etwas grösseren Abstand \(a_G\) zum Punkt A.

Resultierendes Drehmoment

Auch Drehmomente können als Vektorgrösse betrachtet werden und als solche addiert werden. Wie bei den Kräfte können wir auf diese Art alle Kräfte zu einem resultierenden Drehmoment \(\vec{M_{res}}\) addieren. Die Summe aller Drehmomente wirkt ebenfalls gleich, wie alle einzelnen Drehmomente zusammen.

Bevor wir eine Aussage zu einem System machen können, addieren wir alle Kräfte und Drehmomente zusammen und betrachten die resultierenden Kräfte und resultierenden Drehmomente. Haben wir ein verschwindendes resultierendes Drehmoment, so gilt Drehmomentgleichgewicht:

\[ M_{res}=0 \]

Drehmoment als Vektorprodukt

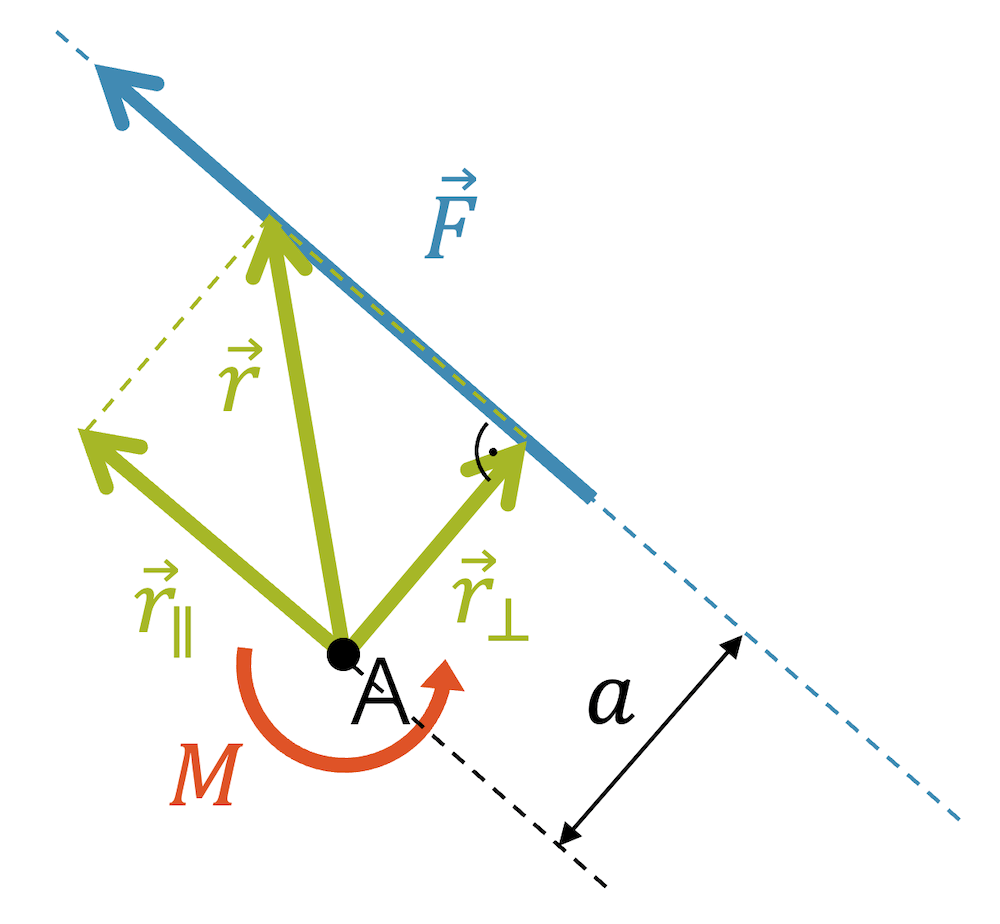
Verwendet man die Definition des Drehmoments mit dem geraden Doppelpfeil, so kann es als Vektor \(\vec{M}\) definiert werden, das einem Vektorprodukt zweier Vektoren entspricht:

\[ \vec{M}=\vec{r} \times \vec{F} \]

Dabei ist der Vektor \(\vec{r}\) der Ortsvektor vom betrachteten Punkt bis zu einem beliebigen Punkt auf der Wirkungslinie der Kraft \(\vec{F}\). Der Ort auf der Wirkungslinie ist unwichtig, da für das Vektorprodukt einzig der Abstand vom betrachteten Punkt zur Wirkungslinie entscheidend ist. Dieser Abstand erhält man, wenn man das Lot auf die Wirkungslinie fällt oder wenn man den Ortsvektor \(\vec{r}\) aufteilt in eine Senkrecht-Komponente \(\vec{r_⟂}\) und eine Parallel-Komponente \(\vec{r_∥}\), dann aber nur den Betrag der Senkrecht-Komponente \(\vec{r_⟂}\) nimmt. Die Parallel-Komponente hat für das Drehmoment keine Bedeutung.