Vervielfachen und Teilen einer Strecke

Vervielfachen einer Strecke

Wie kann eine gegebene Strecke um ein ganzzahliges Vielfaches \(n\) konstruktiv verlängert werden? Ein Abmessen und Multiplizieren der Länge ist nicht erlaubt.

Zuerst ziehen Sie eine Verlängerung. Dann nehmen Sie die Länge der Strecke in den Zirkel und tragen diese Länge vom einen Ende auf die Verlängerung. Dann stechen Sie dort wieder ein und tragen die Strecke nochmals ab, usw. Schliesslich haben Sie die ursprüngliche Strecke vervielfacht (siehe Abbildung).

Teilen einer Strecke

Kann eine gegebene Strecke auch wieder konstruktiv mit einer ganzen Zahl geteilt werden? Ja, hierzu werden wir aber eine Hilfsgerade konstruieren. Wenn Sie am Abend ihren Schatten messen würden, so kann er leicht doppelt so lang sein, wie Sie gross sind. Der Gürtel ist etwa auf der halben Höhe des Körpers. Auch beim Schattenbild ist der Gürtel auf etwa der halben Länge des Schattens. Diese Proportionalität nutzen wir aus.

Wir konstruieren einen beliebigen “Schatten” unserer Strecke, die wir teilen möchten. Die Hilfskonstruktion wird in einem beliebigen spitzen Winkel zur Strecke gezeichnet. Nun nehmen wir ein bekanntes Teilstück und vervielfachen dieses Teilstück auf der Hilfsgeraden mit dem Zirkel. Jetzt haben wir z.B. ein Vierfaches des Teilstücks. Der Endpunkt der vervielfachten Strecke wird mit dem Endpunkt der zu teilenden Strecke (blau) verbunden. Diese Verbindung wird parallel durch die Teilpunkte gezogen, so dass die neuen Parallelen die ursprüngliche Strecke schneiden und in gleich grosse Stücke teilen.

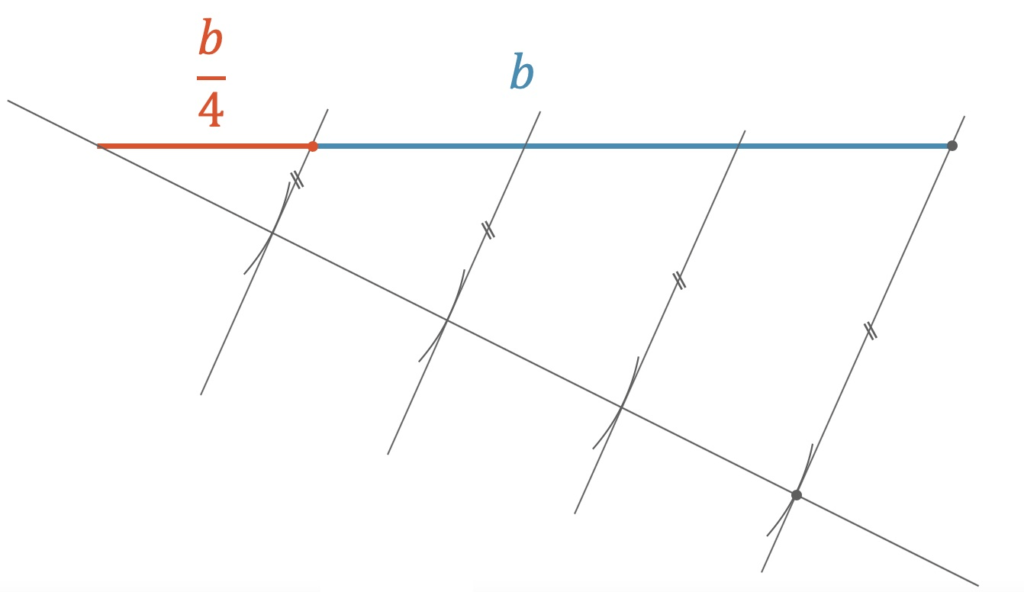
Konstruktion

• Wir zeichnen eine Hilfsgerade in einem beliebigen spitzen Winkel ab dem ersten Endpunkt
• Wir tragen eine beliebige kurze Teilstrecke auf der Hilfsgeraden \(k\)-fach ab und kriegen einen Endpunkt
• Wir verbinden den neuen Endpunkt mit dem zweiten Endpunkt der zu teilenden Strecke
• Wir ziehen die Parallelem durch die Teilungspunkte auf der Hilfsgeraden und erhalten schliesslich den gesuchten Teilungspunkt