Innere Teilung

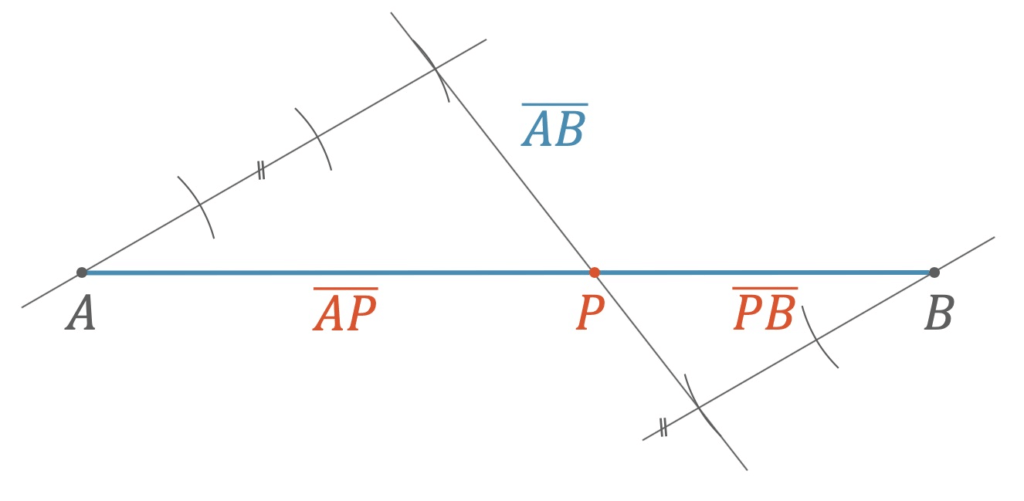
In der obigen Abbildung wird eine gegebene Strecke im Verhältnis \(3:2\) aufgeteilt, d.h. die Strecke \(\overline{AB}\) soll durch den Punkt \(P\) so geteilt werden, dass

\[ \frac{\;\;\overline{AP}\;\;}{\overline{PB}}=\frac{\;3\;}{2} \]

Die Konstruktion ist ähnlich zur einfachen Teilung.

Konstruktion

  • Wir zeichnen zwei Hilfsgeraden in einem beliebigen spitzen Winkel und so dass sie parallel sind.
  • Wir tragen eine beliebige kleine Teilstrecke \(3\)-fach bzw. \(2\)-fach mit dem Zirkel ab.
  • Wir verbinden die beiden Endpunkte und erhalten so den Punkt \(P\), der unsere Strecke im Verhältnis \(3:2\) teilt.

Beispiel

Wie konstruieren Sie 37.5% einer gegebenen Strecke?

Die gegebene Strecke muss in zwei Stücke von 37.5% und 62.5% aufgeteilt werden, bzw.

\[ \frac{\text{37.5\%}}{\text{62.5\%}} = \frac{\;\;\frac{3}{8}\;\;}{\frac{5}{8}} = \frac{3}{5} \]

Wir teilen die Strecke im Verhältnis \(3:5\). Das linke Teilstück entspricht dann \(\frac{3}{8}\) = 37.5%.

Eine gegebene Strecke kann konstruktiv in einem beliebigen Verhältnis \(a:b\) aufgeteilt werden, indem auf zwei parallelen Hilfsgeraden die gleiche beliebige Teilstrecke \(a\)-fach bzw. \(b\)-fach mit dem Zirkel abgetragen wird. Die Verbindung der beiden Endpunkte auf den Hilfsgeraden gibt uns den gesuchten Teilungspunkt \(P\).

Wenn dieser Teilungspunkt auf der Strecke ist, spricht man von innerer Teilung.

Äussere Teilung

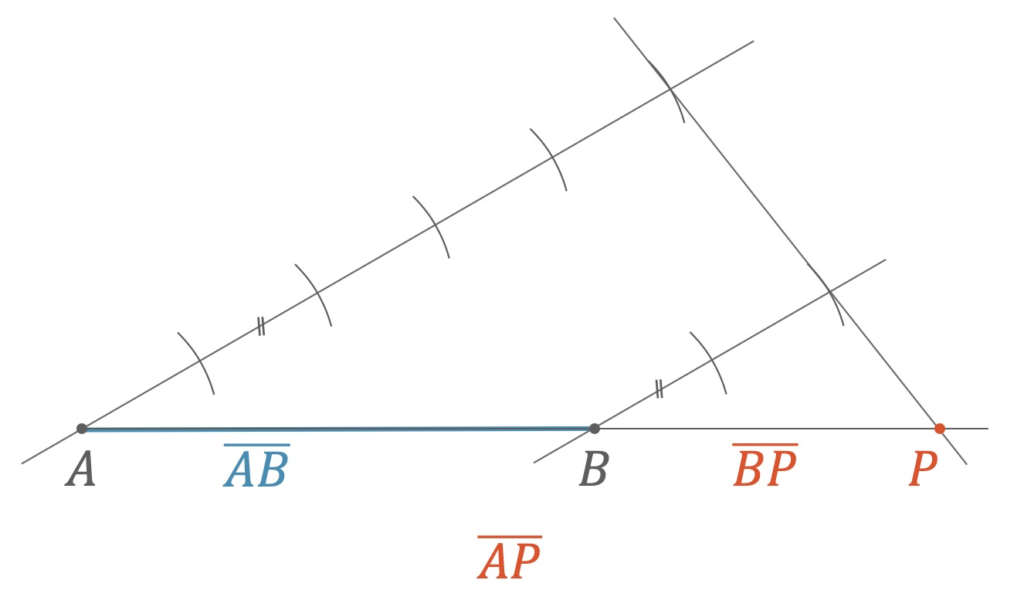
Eine Strecke kann auch geteilt werden, so dass der Punkt der Teilung \(P\) nicht zwischen \(A\) und \(B\), sondern ausserhalb der gegebenen Strecke zu liegen kommt. Wie bei der inneren Teilung, vergleichen wir die beiden Teilstrecken \(\overline{AP}\) und \(\overline{PB}\). Für die äussere Teilung in der obigen Abbildung gilt:

\[ \frac{\;\;\overline{AP}\;\;}{|\overline{PB}|}=\frac{\;\;\overline{AP}\;\;}{|\overline{BP}|}=\frac{\;5\;}{2} \]

Beachten Sie, dass durch die Umkehrung von \(\overline{PB}\) zu \(\overline{BP}\), das Vorzeichen wechselt. Da wir uns hier nicht um das Vorzeichen kümmern möchten, haben wir die Betragsstriche hinzugefügt.

Konstruktion

  • Wir zeichnen zwei Hilfsgeraden in einem beliebigen spitzen Winkel und so dass sie parallel sind.
  • Wir tragen eine beliebige kleine Teilstrecke \(5\)-fach bzw. \(2\)-fach mit dem Zirkel ab.
  • Wir verbinden die beiden Endpunkte und erhalten so eine neue Hilfsgerade, die wir verlängern
  • Der Schnittpunkt der neuen Hilfsgeraden mit der Verlängerung der Strecke gibt uns den Punkt \(P\), der unsere Strecke im Verhältnis \(5:2\) teilt.

Zu einer gegebenen Strecke kann konstruktiv ein Teilungspunkt \(P\) gefunden werden, dessen Abstände zu den beiden Endpunkten \(A\) und \(B\) ein bestimmtes Verhältnis \(a:b\) einnehmen. Wenn dieser Teilungspunkt nicht zwischen den Endpunkten, sondern ausserhalb der Strecke und auf deren Verlängerung zu liegen kommt, spricht man von äusserer Teilung der Strecke.

Zwei parallele Hilfsgeraden mit \(a\)-facher und \(b\)-facher Teilstrecke ergeben zwei Endpunkte. Die Verbindung dieser beiden Endpunkte, verlängert, schneidet die Verlängerung der Strecke, was zum Teilungspunkt \(P\) führt.

Aufgabensammlung

  • Teilung einer Strecke (5001) – Aufg. 1

David John Brunner

Lehrer für Physik und Mathematik, Zürich | Mehr erfahren

Frage oder Kommentar?

Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.

Kommentar oder Frage schreiben