Das Wichtigste in Kürze
Die allgemeine Form der Gleichung einer Kugel \(K\) in Koordinatenform lautet:
\[ K \colon \;\; (x-Z_x)^2 + (y-Z_y)^2 + (z-Z_z)^2 = r^2 \]
Die Kugel ist eine Punktschar aller Punkte \(Q(x,y,z)\), die zum Zentrum \(Z(Z_x,Z_y,Z_z)\) alle den gleichen Abstand, nämlich den Radius \(r\) haben. Sie ist eine flächige Punktschar wie eine Ebene, jedoch als Kugel gekrümmt.
Die Punkte auf der Kugeloberfläche haben eines gemeinsam: Sie haben alle den gleichen Abstand zum Kugelzentrum \(Z\) und dieser Abstand heisst Radius der Kugel \(r\). Die Kugel ist in drei Dimensionen das, was der Kreis in zwei Dimensionen ist. Wir können deshalb unsere Überlegungen vom Kreis jetzt auf drei Dimensionen übertragen.
Die nachstehende Grafik zeigt eine Kugel mit Radius \(r=2\). Die Punkte \(P_1(2,0,0)\), \(P_2(0,2,0)\) und \(P_3(0,0,2)\) haben alle den Abstand \(r=2\) zum Zentrum im Ursprung \(Z(0,0,0)\). Wenn wir irgendeinen Punkt \(Q(Q_x,Q_y,Q_z)\) auf der Kugeloberfläche betrachten, dann hat auch dieser Punkt einen Abstand \(r=2\) zum Zentrum.
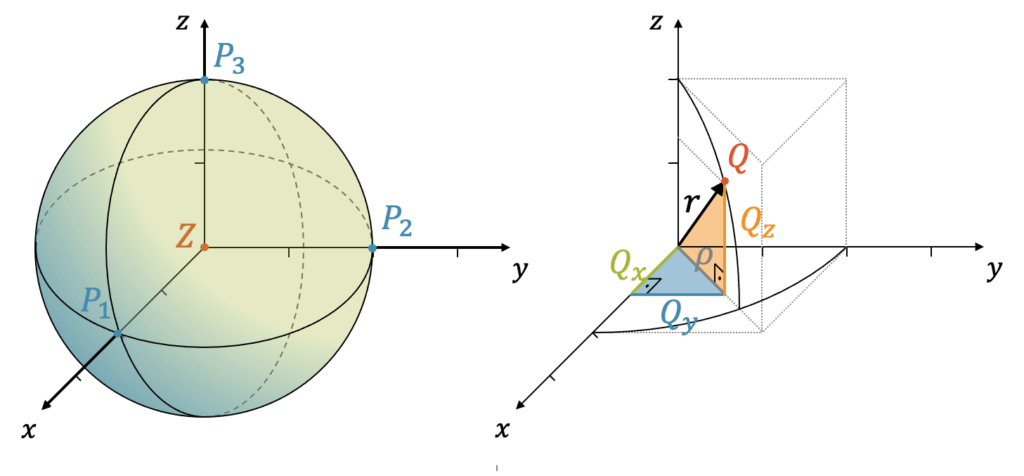
Zuerst benutzen wir den Satz des Pythagoras und berechnen die graue Hypotenuse \(\rho\) des liegenden rechtwinkligen Dreiecks (blau eingefärbt):
\[ \rho = \sqrt{(Q_x)^2+(Q_y)^2} \]
Jetzt können wir das stehende rechtwinklige Dreieck (orange eingefärbt) berechnen:
\[ r = \sqrt{\rho^2+(Q_z)^2} \]
Wenn wir den Ausdruck für \(\rho\) von oben einsetzen, erhalten wir:
\[ r = \sqrt{\Big( (Q_x)^2+(Q_y)^2 \Big)+(Q_z)^2} \]
Ohne Klammern und quadriert haben wir damit:
\[ r^2 = (Q_x)^2 + (Q_y)^2 + (Q_z)^2 \]
Für irgendeinen Punkt \(Q\) auf der Kugel gilt im allgemeinen Fall wieder:
\[ \overrightarrow{ZQ} = \overrightarrow{OQ} – \overrightarrow{OZ} \]
Die linke Seite hat den Vektor \(\overrightarrow{ZQ}\), der die Rolle des Radius übernimmt. Sein Betrag bzw. seine Länge entspricht natürlich \(r\). Die rechte Seite ist gleich diesem Vektor und somit ist die Länge der Vektordifferenz auf der rechten Seite auch gleich \(r\).
\[ r = \Big|\overrightarrow{ZQ}\Big| = \Big|\overrightarrow{OQ} – \overrightarrow{OZ}\Big| \]
\[ r = \sqrt{(ZQ_x)^2 + (ZQ_y)^2 + (ZQ_z)^2} \]
\[ = \sqrt{(x-Z_x)^2 + (y-Z_y)^2 + (z-Z_z)^2} \]
Wir quadrieren und erhalten die Gleichung der Kugel. Sie ist eigentlich genau wie die Kreisgleichung, jedoch mit einer Dimension mehr:
\[ (x-Z_x)^2 + (y-Z_y)^2 + (z-Z_z)^2 = r^2 \]
Für die oben abgebildete Kugel haben wir \(Z(Z_x,Z_y,Z_z)\), d.h. \(Z_x=0\), \(Z_y=0\) und \(Z_z=0\) und \(r=2\). In die Gleichung eingesetzt, erhalten wir:
\[ x^2 + y^2 + z^2 = 4 \]
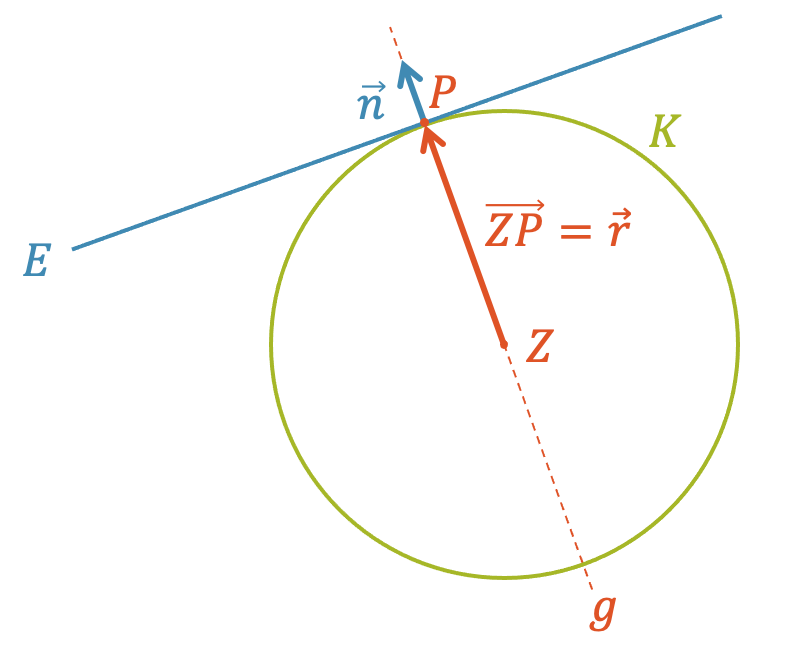
Beispiel: Kugel berührt Ebene
Finde die Gleichung der Kugel \(K\), die das Zentrum in \(Z(-4,1,1)\) hat und die die Ebene \(E\) gerade berührt.
\[ E \colon \;\; 4x – 2y – z = 2 \]
Aufgabensammlung
Weitere Links
Kugel (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.