
Energieaustausch Schwingungen / Wellen
Schwingungen können Wellen auslösen und umgekehrt. Bei einer Schwingung ist Energie in einem System “eingesperrt”. Sie wechselt nur periodisch zwischen zwei Energieformen hin und her. Wellen transportieren Energie, d.h. eine Schwingung kann über die Erzeugung einer Welle ihre Energie abgeben.
Wir schauen uns ein vereinfachtes Beispiel an: Ein Elektron befindet sich in einer Metallstange. Mit einem oszillierenden elektrischen Feld wird dieses Elektron beschleunigt. Es wird in Schwingung gebracht.
Beschleunigte elektrische Ladung strahlt eine elektromagnetische Welle ab. Wenn wir auf eine Wasseroberfläche mit einem Finger in regelmässigen Abständen “tippen” würden, würden in regelmässigen Abständen Kreiswellen von diesem Punkt ausgehen.
Beim elektromagnetischen Feld ist das ähnlich. Die elektromagnetische Welle breitet sich als Kugelwelle im Raum aus. Wir schauen uns jetzt aber nur diejenige Welle an, die zu einer anderen Metallstange führt. In dieser zweiten Metallstange sitzt ein Elektron, das durch die eingehende Welle in Schwingung gebracht wird.

Wir wissen, dass eine elektromagnetische Welle ein elektrisches und ein magnetisches Feld besitzt, die beide senkrecht aufeinander stehen. Der Poynting-Vektor, den wir von der elektromagnetischen Welle erhalten, ist in der Richtung der Bewegung der Welle (Wellengeschwindigkeit \(c\)) gerichtet.
Der Poynting-Vektor besagt auch, dass wir hier einen Fluss von Energie pro Fläche und Zeit haben. Die erste Schwingung gibt demnach Energie an die Welle ab. Diese transportiert diese Energie ab und gibt ihre Energie dem zweiten Elektron wieder ab.
An dieser Stelle magst du dich fragen, ob denn ein um den Atomkern kreisendes Elektron nicht auch eine elektromagnetische Welle aussenden sollte? Tatsächlich hat sich die Welt der Physik diese Frage gestellt und das Elektron müsste tatsächlich eine solche Welle aussenden. Es ist aber ebenfalls klar, dass es das nicht tut. Atome strahlen keine elektromagnetischen Wellen einfach so ab und die damit verlorene Energie würde irgendwann zu Ende gehen.
liegt im quantenmechanischen “Zustand” des Elektrons um den Atomkern herum, der keine elektromagnetische Welle erzeugt.
Die Erklärung lieferte schliesslich die Quantenmechanik. Das Elektron kreist nicht wirklich um den Kern herum, sondern befindet sich irgendwo in der Umgebung des Kerns, aber niemand weiss genau wo es sich genau befindet. Den Aufenthaltsort des Elektrons können wir am besten mit einer Wellenfunktion beschreiben (Wellennatur des Elektrons), was mehr einer Wahrscheinlichkeitsverteilung für den Aufenthaltsort entspricht.
Energie einer periodischen Seilwelle
Wenn wir an einem mehr oder weniger gespannten Seil ein Stück davon quer zur Richtung des Seils bewegen, so wird entlang des Seils eine sog. Seilwelle ausgesendet. Das Gleiche geschieht übrigens auch beim Zupfen, Streichen oder Schlagen einer Saite bei jedem Saiteninstrument oder Klavier.
Wenn wir in der obigen Grafik ein kleines Stück Seil anschauen, so hat es eine kleine Masse \(dm\). Diese kleine Masse ist im Seil eingebaut und kann sich nur auf und ab bewegen. Die vertikale Geschwindigkeit \(v_y\) ist der einzige Beitrag zur kinetischen Energie, die ebenfalls sehr klein ist, da es sich ja um sehr wenig Masse handelt:
\[ dE_{kin} = \frac{1}{2} \cdot dm \cdot v_y^2 \]
Entlang des Seils kann die Welle sich bewegen und zwar sogar recht schnell. Das ist übrigens ganz typisch für Wellen. Die an der Welle beteiligten Massen oder Teilchen bewegen sich eigentlich nicht wirklich – das tut die Welle! Sie bewegt die Energie bzw. gibt sie weiter.
Wir ersetzen die kleine Masse mit folgendem Ausdruck:
\[ dm = \mu \cdot dx \]
Dabei ist \(\mu\) eine Längendichte, d.h. Masse pro Länge für dieses Seil. \(dx\) ist jetzt die Länge des kleinen Stücks Seil.
Wir setzen das ein in den Ausdruck der kinetischen Energie:
\[ dE_{kin} = \frac{1}{2} \cdot \mu \cdot dx \cdot v_y^2 \]
Wie oder was verändert die kinetische Energie eines kleinen Seilstücks? Es ist die Welle, die an ihm vorbeizieht, die Energie mitbringt und auch wieder mitnimmt. Das Seilstück der Länge \(dx\) wird in der kurzen Zeit \(dt\) durch die Welle abgestreift. Wir leiten die kinetische Energie nach der Zeit ab und erhalten:
\[ \frac{dE_{kin}}{dt} = \frac{1}{2} \cdot \mu \cdot \frac{dx}{dt} v_y^2 \]
Für das Abstreifen von \(dx\) in der Zeit \(dt\) schreiben wir: \(c = \frac{dx}{dt} = \ddot{x}\). Das gibt uns:
\[ \frac{dE_{kin}}{dt} = \frac{1}{2} \cdot \mu \cdot c \cdot v_y^2 \]
Die Seilwelle ist eine transversale Welle und die Auslenkung ist in \(y\)-Richtung, währenddem die Welle selber in \(x\)-Richtung verläuft. Wir können für eine solche Welle den folgenden Ansatz einer periodischen Welle nehmen:
\[ y(x,t) = A \cdot \sin(kx – \omega t) \]
Betrachten wir beispielsweise die Position \(x=0\) erhalten wir die harmonische Schwingung:
\[ y(0,t) = A \cdot \sin(\omega t) \]
Die Geschwindigkeit, mit welcher sich das Seilstück auf- und ab bewegt, ist \(v_y\) und entspricht der zeitlichen Ableitung der Position \(y(0,t)\):
\[ v_y = \frac{d}{dt} y(0,t) = -A\omega \cos(\omega t) \]
Wir setzen das oben ein und erhalten:
\[ \frac{dE_{kin}}{dt} = \frac{1}{2} \cdot \mu c \cdot A^2 \omega^2 \cdot \cos^2(\omega t) \]
Die Kosinusfunktion schwingt zwischen -1 und +1. Ihr Quadrat schwingt zwischen 0 und 1, d.h. über die Zeit gemittelt, erhalten wir \(\frac{1}{2}\). Für die zeitliche Mittelung setzen wir die Spitzklammern:
\[ \Big\langle \frac{dE_{kin}}{dt} \Big\rangle = \frac{1}{2} \cdot \mu c \cdot A^2 \omega^2 \cdot \frac{1}{2} \]
Die kinetische Energie des betrachteten Seilstücks wird von der Welle geliefert. Diese Energielieferung pro Zeit \(\frac{dE_{kin}}{dt}\) entspricht einer Leistung \(P\). wir schreiben deshalb:
\[ P = \frac{1}{4} \cdot \mu c \cdot A^2 \omega^2 \]
Die Leistung der Seilwelle nimmt mit dem Quadrat der Amplitude \(A\) und mit dem Quadrat der Kreisfrequenz \(\omega\) zu.
Je grösser und stärker die Schwingung ist, die die Welle erzeugt, desto mehr Leistung bringt die Seilwelle mit.
Intensität
Unter Intensität verstehen wir in der Physik die Leistung pro Fläche. Da die Leistung als Energie pro Zeit definiert ist, ist die Intensität die Energie, die pro Zeit und Fläche auftrifft.
Intensität: Ist die Energie (in Joule), die pro Zeit (pro Sekunde) und pro Fläche (pro Quadratmeter) auftrifft.
Als erstes Beispiel nehmen wir die Strahlungsintensität der Sonne. Es sind elektromagnetische Wellen, die Energie von der Sonne zur Erde bringen. Wenn auch nicht die einzige Energiequelle, ist es doch die für uns wichtigste Energiequelle. Selbst die fossilen Energieträger enthalten letztlich Sonnenstrahlung aus einer anderen Zeit.
Die Sonne strahlt immer gleich stark aus, d.h. die Energie pro Zeit ist immer gleich. Beim Beispiel eines Kaminfeuers können wir uns aber vorstellen, dass ein stark brennendes Feuer mehr Energie pro Zeit aussendet, als ein fast erloschenes Feuer.
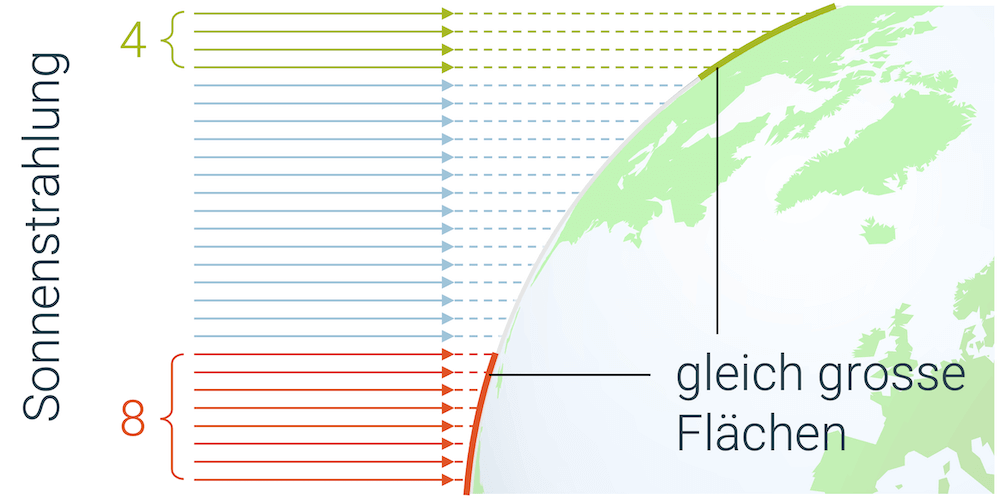
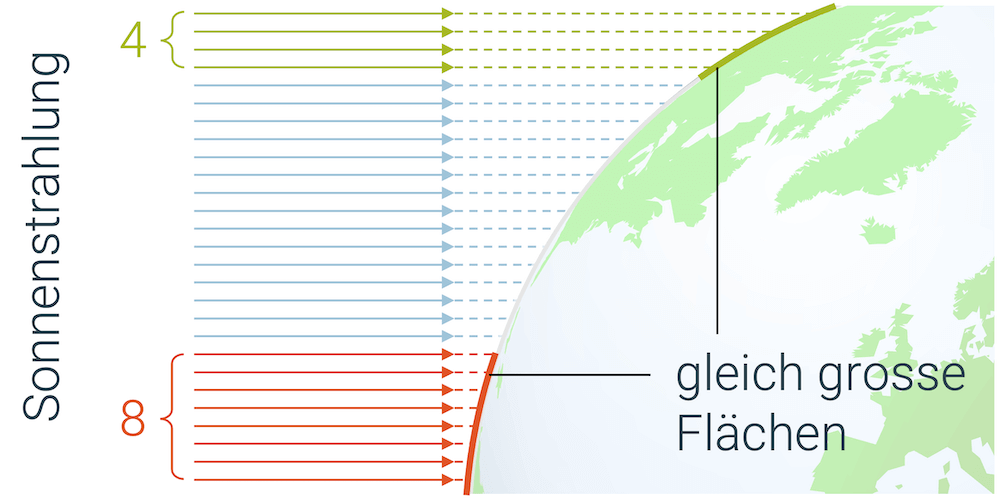
Den Einfluss der Fläche können wir uns wie folgt erklären: Wir wissen, dass die Sonnenstrahlung am Äquator besonders stark ist. Eigentlich ist die Sonnenstrahlung immer überall gleich stark. Am Äquator trifft sie nur fast senkrecht (Einfallswinkel 90°) auf die Erdoberfläche, während sie in unseren Breiten unter einem grösseren Einfallswinkel auftrifft.
Nehmen wir “ein Stück” Sonnenstrahlung, als hätten wir ein einziges Dachfenster in einem riesigen Dach, so trifft dieses Stück Strahlung am Äquator auf einer relativ kleinen Fläche auf. Wenn aber die Sonne unter einem flacheren Winkel scheint, so wird das Licht auf eine grössere Fläche verteilt und ist deshalb weniger konzentriert. Die Intensität ist im zweiten Fall weniger gross.
Nehmen wir eine Lupe, so können wir die Lichtstrahlen, die auf die Lupe auftreffen im Brennpunkt aufkonzentrieren und dort eine sehr hohe Intensität erreichen.
Warum ist die Strahlung der Sonne viel intensiver als die Strahlung von Sternen? Unsere Sonne ist ja ein Stern. Obwohl andere Sterne z.t. viel grösser und heller sind, kommt bei uns viel weniger Energie an, als von der Sonne. Der Grund liegt offensichtlich im unterschiedlich grossen Abstand zur Erde.
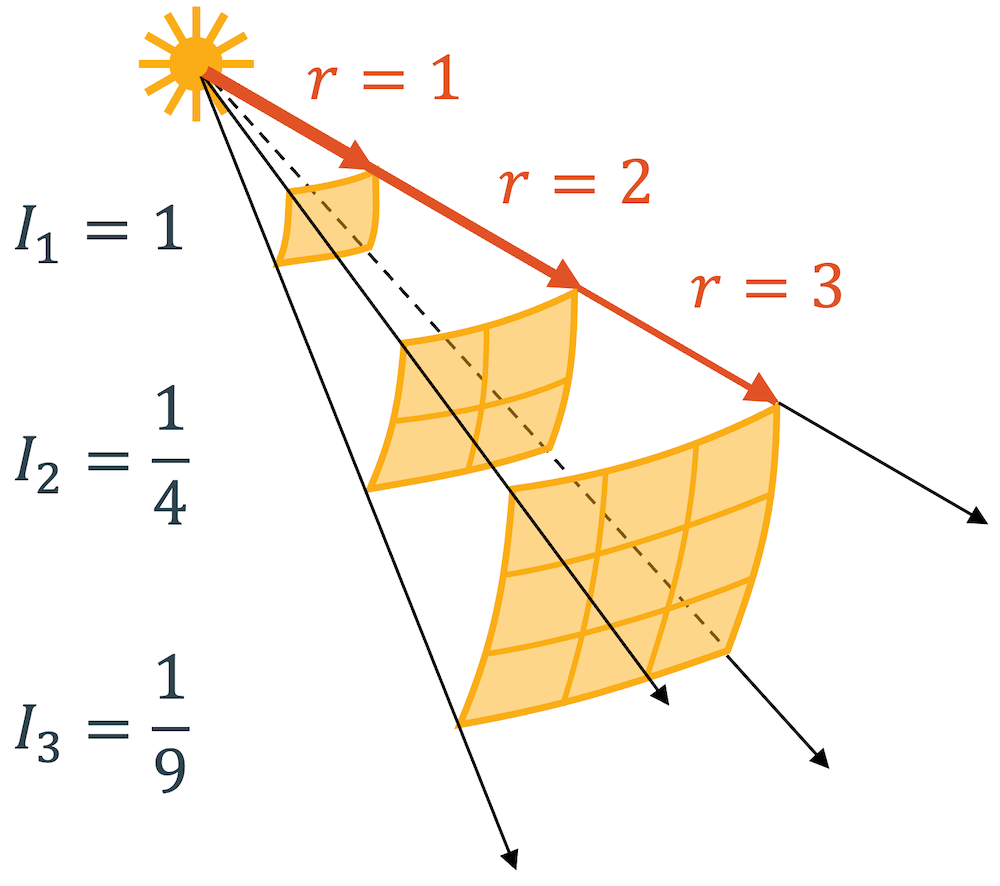
Wenn wir uns nachfolgende Grafik anschauen, sehen wir, dass die Strahlung im Abstand 1 sich auf eine einfache Fläche konzentriert, im Abstand 2 sie auf eine vierfache Fläche verteilt und im Abstand 3 die Fläche bereits 9-fach ist.
Wir können uns auch eine Kugel vorstellen. Die Fläche einer Kugel wird mit folgender Formel berechnet:
\[ A = 4 \pi r^2 \]
Wenn die Kugel einen Radius \(r=2\) statt \(r=1\) hat, dann ist ihre Oberfläche wegen dem Quadrat nicht doppelt, sondern eben 4-fach.
Wenn als die Fläche, durch welche die Strahlung durchtritt, mit dem Quadrat des Abstands zunimmt, dann nimmt die Intensität entsprechend mit dem Quadrat des Abstands ab. Die Intensität ist im Abstand \(r=2\) genau 4-mal kleiner als im Abstand \(r=1\).
Das gilt nicht nur für das Licht, sondern für alle Wellen, die sich im Raum als Kugelwellen ausbreiten, z.B. Schall bei einer Explosion. Wenn wir die Intensität der Welle klein halten möchten, können wir sie leicht reduzieren, indem wir von der Quelle mehr Abstand halten. Mit 10-fachem Abstand ist die Intensität bereits 100-fach kleiner.
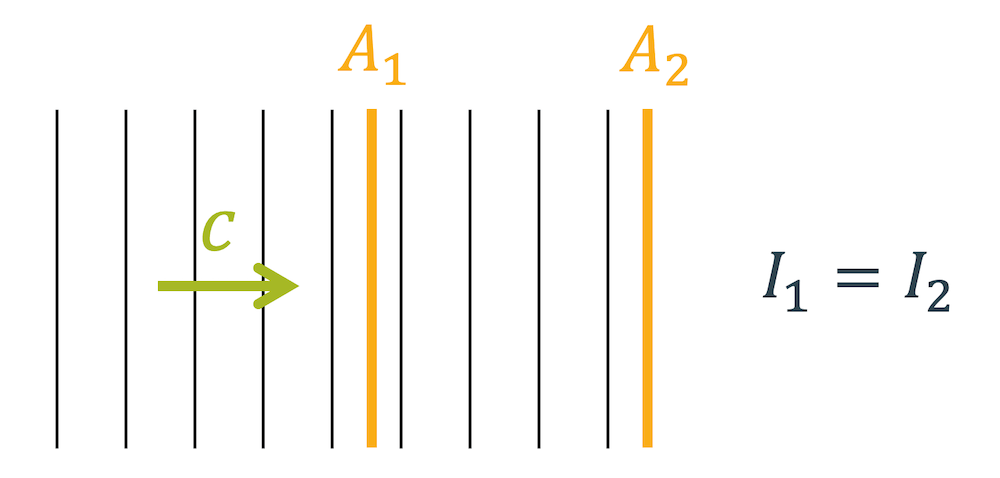
Bei der Kugelwelle nimmt die Fläche mit dem Quadrat zu, so dass die Intensität entsprechend abnimmt. Wie ist das dann bei ebenen Wellen? Die Fläche der ebenen Welle ist nicht nur eben, sondern auch konstant. Damit bleibt die Intensität gleich, unabhängig vom Abstand, den wir von der Quelle haben.
Wenn wir die Lichtstrahlen mit einem Konkavspiegel oder einer Sammellinse parallel machen, erhalten wir näherungsweise ebene Wellen, die dann sehr grosse Distanzen fast verlustfrei überwinden können. Sog. Richtstrahl-Antennen machen genau das. Ein Parabolspiegel dient als Konkavspiegel und die Quelle wird in den Brennpunkt gestellt, so dass die Strahlen als parallele Strahlen reflektiert werden. Von da an kann der Richtstrahl auf die Empfängerantenne gerichtet werden.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.