Die Sonne sendet ihre Lichtstrahlen in alle Richtungen. Wenn wir genug weit weg wären, wäre die Sonne nur ein kleiner Stern am Himmel, eine Punktquelle von Licht. Bereits schon vom Neptun aus gesehen, dem äussersten Planeten in unserem Sonnensystem, ist die Sonne nichts mehr als ein heller Stern.
Die Erde ist nach Merkur und Venus der drittnächste Planet zur Sonne. Bei uns hat die Sonne noch eine Ausdehnung am Himmel – wir reden von der Sonnenscheibe und nicht von einem Sonnenpunkt. Die Sonne ist aber unglaublich viel grösser als wir uns das je vorstellen könnten, wenn wir sie z.B. beim Sonnenuntergang am Horizont betrachten. Eine Gegenüberstellung der beiden sähe etwa so aus:

Der Durchmesser der Erde \(d_E\) beträgt ca. 12’742 km, also etwa \(1.3 \cdot 10^4 \; \mathrm{km}\). Die Sonne hat einen Durchmesser \(d_S\) von \(1.4 \cdot 10^6 \; \mathrm{km}\). Das Verhältnis der beiden Durchmesser ist demnach:
\[ \frac{d_S}{d_E} = \frac{1.4 \cdot 10^6}{1.3 \cdot 10^4} \approx 10^2 \]
Die Sonne ist somit rund hundert mal grösser als die Erde. Wenn wir die Erde nahe an der Sonne zeichnen, wie in der folgenden Skizze, so können wir uns vorstellen, dass sie ein riesiger Feuerball ist mit unzähligen Punkquellen, die selber Licht in alle Richtungen abgeben. Diese Punktquellen können am äussersten Rand liegen. In unserer Skizze ergeben die beiden extremen Sonnenstrahlen, die gerade noch zur Erde gehen, ein gleichschenkliges Dreieck mit einem Scheitelwinkel \(\alpha\)
\[ \alpha \approx 20^\circ \]
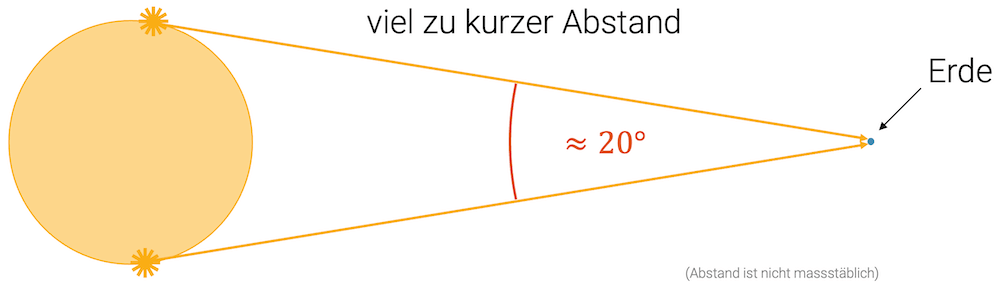
Diese Skizze ist aber falsch, denn der Abstand zwischen Sonne und Erde ist verhältnismässig viel grösser als in dieser Skizze dargestellt. Er ist sogar so gross, dass wir Mühe haben, ihn korrekt darzustellen.
Wenn wir den Abstand korrekt darstellen möchten, dann würde die Skizze etwa wie folgt aussehen. Wir müssen dazu so stark herauszoomen, dass die Erde gar nicht mehr zu erkennen ist. Wir stellen uns einfach ein hundert mal kleineres Pünktchen vor, als die Sonne links. Das gleichschenklige Dreieck mit Scheitelwinkel \(\alpha\) ist jetzt extrem lang gezogen. Entsprechend ist der Scheitelwinkel unglaublich klein geworden. Er beträgt nur noch etwa
\[ \alpha \approx 0.5^\circ \]

Die Folge ist, dass alle Strahlen, die von der Sonne auf die kleine Erde auftreffen, höchstens um ein halbes Grad von einander abweichen. Das ist so wenig, dass wir näherungsweise annehmen können, dass die Sonnenstrahlen auf der Erde parallel sind (\(\alpha \approx 0^\circ\)).
Die Sonne strahlt als Kugel in alle Richtungen ab (wie die Sonne in der Kinderzeichnung)
Da die Sonne auf der Erde unter einem sehr kleinen Winkel von \(\alpha \approx 0.5^\circ\) gesehen wird, können wir näherungsweise davon ausgehen, dass die Sonnenstrahlen auf der Erde parallel sind (\(\alpha \approx 0^\circ\)).
Sobald wir wieder grössere Dimensionen betrachten und die Sonne ein “kleiner Feuerball” in der Zeichnung ist, müssen wir wieder alle Strahlungsrichtungen annehmen und wir zeichnen die Sonnenstrahlen nicht mehr parallel. Insbesondere müssen wir daran denken, dass der Feuerball aus unzähligen Punktquellen besteht, die ihrerseits in alle Richtungen abstrahlen.
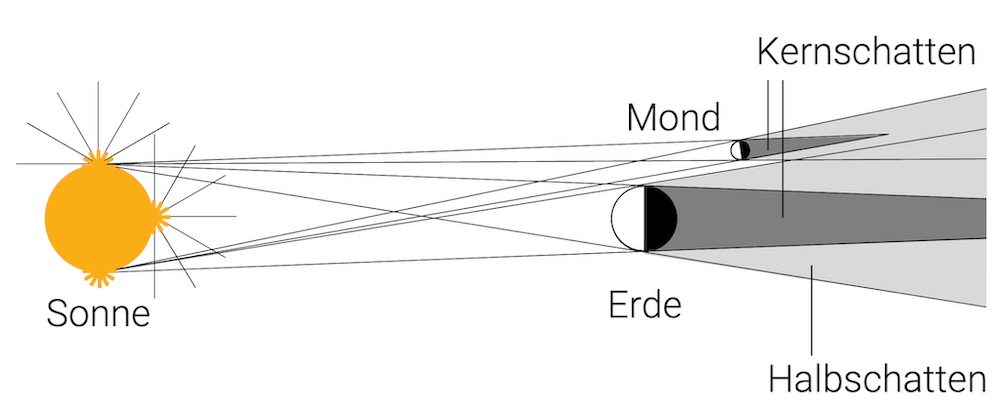
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.