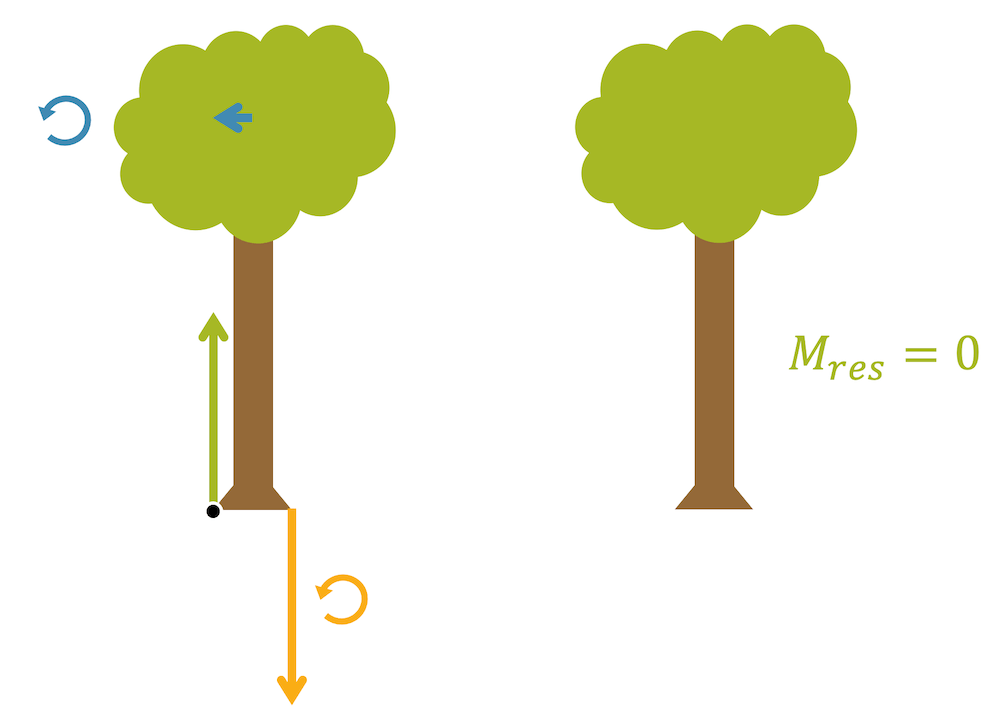
Addieren wir alle Drehmomente, die auf ein System oder einen Gegenstand wirken, erhalten wir das resultierende Drehmoment \(\vec{M_{res}}\). Wenn dieses resultierende Drehmoment verschwindet, haben wir den speziellen Fall des Drehmomentgleichgewichts, in welchem sich alle wirkenden Drehmomente in Summe aufheben:
\[ \vec{M_{res}} = 0 \]
Wie das Kräftegleichgewicht, ist das Drehmomentgleichgewicht eine wichtige Voraussetzung für die Statik.
Zusätzliches Kriterium zum Kräftegleichgewicht
In der Statik geht es darum, mechanische Systeme zu beschreiben oder zu berechnen. Es handelt sich, im Gegensatz zur Dynamik um Systeme, die sich nicht bewegen, wie z.B. Gebäude, Brücken, Türme etc. Das Drehmoment ist hier eine wichtige Ergänzung zur Kraft, wie am Beispiel eines an der Tischkante kippenden Würfels gezeigt wird.
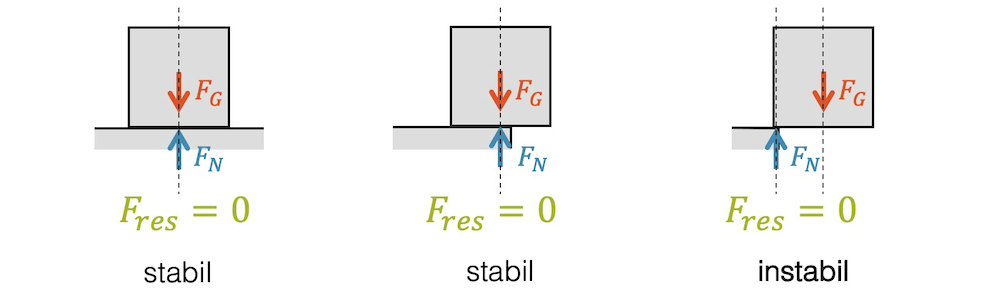
Betrachten wir die drei Situationen, die oben abgebildet sind, so erkennen wir zwei stabile Situationen (links und mitte) und die rechte (instabile) Situation, in welcher der Würfel von der Tischkante herunterfallen wird.
Mit den Kräften, d.h. mit dem Kräftegleichgewicht allein, können wir diese Instabilität nicht voraussagen. Alle drei Situationen haben eine verschwindende resultierende Kraft \(F_{res}\). Gemäss Newtons Erstem Gesetz dürften die Würfel in allen drei Situationen keine Beschleunigung erfahren, sondern müssten in Ruhe bleiben. Das stimmt nur in den beiden Fällen links und in der Mitte, jedoch nicht im Fall rechts.
Wir erkennen einen Unterschied: Die Wirkungslinien der Gewichts- und Normalkraft sind gleich, ausser in der instabilen Situation rechts.
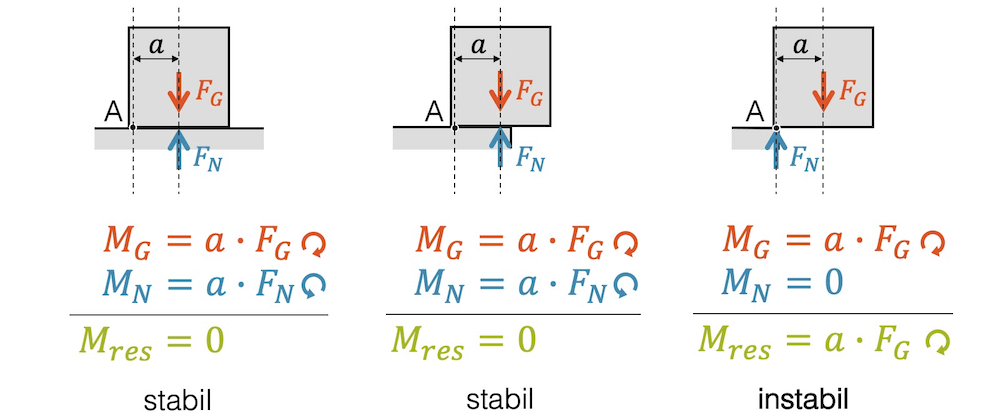
Wir betrachten nun das Drehmoment der beiden Kräfte. Zuerst erinnern wir uns aber, dass die Gewichts- und die Normalkraft vom Betrag her, gleich sein müssen: \(F_G = F_N\).
In den ersten beiden Situationen (links und mitte) haben wir einmal ein Drehmoment \(M_G\) aufgrund der Gewichtskraft. \(M_G\) zeigt im Uhrzeigersinn. Das Drehmoment der Normalkraft ist vom Betrag her gleich gross, da die Kraft gleich stark ist und der Abstand \(a\) auch gleich ist. Die Richtung ist jedoch umgekehrt: Gegenuhrzeigersinn.
Wir addieren die beiden Drehmomente und erhalten für das resultierende Drehmoment: \(M_{res}=0\), da sich die beiden gleich grossen Drehmomente genau aufheben.
In der Situation rechts kommt der Ort der beiden Wirkungslinien zum Tragen. Die Gewichtskraft erzeugt wieder das Drehmoment \(M_G\) wie vorhin in den beiden anderen Situationen. Das Drehmoment der Normalkraft \(M_N\) ist dieses Mal aber verschwindend und hebt dadurch \(M_G\) nicht mehr auf. Wir erhalten ein resultierendes Drehmoment, das nicht mehr null ist: \(M_{res} = a \cdot F_G\).
Wenn wir analysieren wollen, ob ein System stabil ist, d.h. trotz der Kräfte nicht beschleunigt wird, sondern in Ruhe verbleibt, brauchen wir nicht nur das Kräftegleichgewicht mit der resultierenden Kraft \(F_{res}=0\) zu untersuchen, sondern auch das Drehmomentgleichgewicht mit dem resultierenden Drehmoment \(M_{res}\).
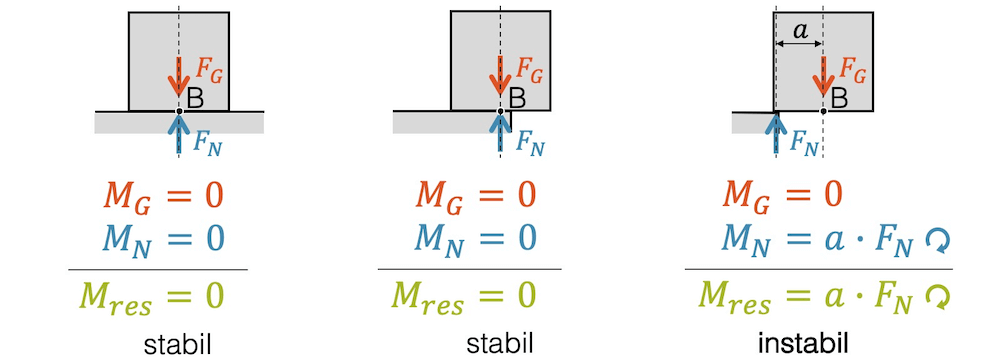
Es wird dich vermutlich erstaunen, dass der Punkt A willkürlich gesetzt werden kann, wo doch jedes Drehmoment von ihm abhängig ist. Im folgenden Beispiel soll gezeigt werden, dass wir auch einen anderen Punkt B betrachten können und wir trotzdem zu dem genau gleichen Ergebnis gelangen.
Wir setzen z.B. B so, dass wir in den ersten beiden Situationen keine Drehmomente erhalten. Die beiden resultierenden Drehmomente ergeben so auch null.
In der dritten Situation verschwindet dieses Mal das Drehmoment \(M_G\) der Gewichtskraft, da die Kraft durch den Punkt B geht. Dafür erhalten wir ein Drehmoment aufgrund der Normalkraft, das wir das letzte Mal nicht hatten. Für das resultierende Drehmoment in der Situation rechts erhalten wir somit: \(M_{res} = a \cdot F_N\). Nun erinnern wir uns, dass \(F_G = F_N\), d.h. wir haben auch hier wieder das genau gleiche Resultat bekommen, wie für den Punkt A.
In der Statik verlangen wir deshalb, dass ein ruhendes System durch Krafteinwirkung nicht beschleunigt wird (z.B. umkippt), sondern dass es in Ruhe ist und in Ruhe verbleibt. Mit Newtons Erstem Gesetz verlangen wir eine verschwindende resultierende Kraft \(\vec{F_{res}}=0\), d.h. Kräftegleichgewicht:
\[ F_{res}=0 \]
Zusätzlich verlangen wir aber auch ein verschwindendes resultierendes Drehmoment, d.h. Drehmomentgleichgewicht:
\[ M_{res}=0 \]
Wenn das Kräfte- und das Drehmomentgleichgewicht in allen Richtungen gilt, ist das System statisch stabil, d.h. es wird nicht beschleunigt. Das gilt natürlich auch nur unter der Annahme, dass die Kräfte und Drehmomente vom Material ausgehalten werden. Ist das Material zu schwach, wird das System nachgeben.
Mit Hilfe des Kräfte- und Drehmomentgleichgewicht können Ingenieure und Architekten die Kräfte berechnen, mit welchen die zukünftige Konstruktion belastet sein wird und entsprechende Vorkehrungen treffen, so dass diese Kräfte vom gewählten Material auch sicher aufgenommen werden können.
Beispiel
Welche Kräfte wirken am grossen Urwaldbaum, damit er trotz seitlicher Windkraft \(F_4\) stehen bleibt?
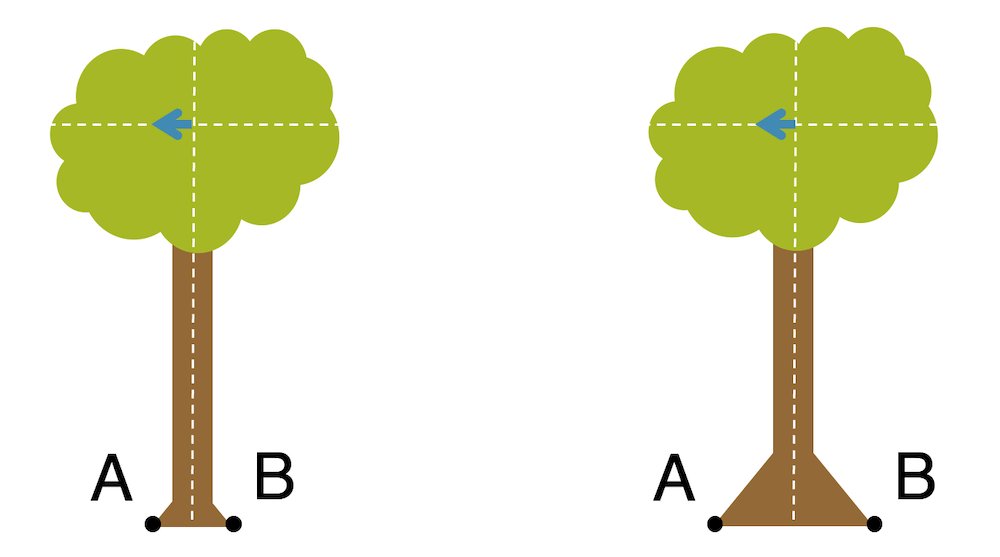
Wir wählen den Punkt A an der Wurzel und erhalten so das erste Drehmoment der Windkraft, wobei wir \(h\) für die mittlere Höhe annehmen, an welcher die Windkraft angreift:
\[ M_1 = h \cdot F_4 \]
Das Drehmoment \(M_1\) zeigt in unserer Zeichnung im Gegenuhrzeigersinn. Wäre es das einzige Drehmoment, so wäre \(M_{res} = M_1\) und der Baum würde beim ersten Windstoss umfallen und zwar genau so: Im Gegenuhrzeigersinn.
Damit das nicht geschieht, braucht es ein Drehmoment, das zum Drehmomentgleichgewicht führt, d.h. \(M_{res} = 0\). Das zusätzliche Drehmoment muss genau gleich gross sein wie \(M_1\), aber entgegengesetzt in der Richtung.
Betrachten wir die drei Kräfte, die an der Wurzel wirken: \(F_1\), \(F_2\) und \(F_3\). Einzig \(F_2\) könnte dieses neue Drehmoment erzeugen. \(F_1\) und \(F_3\) können für den Punkt A kein Drehmoment erzeugen, da deren Wirkungslinien durch A führen. Die Wirkungslinie von \(F_2\) führt in einem Abstand \(b\) von A, der der Breite der Wurzel entspricht:
\[ M_2 = b \cdot F_2 \]
Das Drehmoment \(M_2\) zeigt im Uhrzeigersinn. Da \(b\) gegeben ist, muss der Betrag von \(F_2\) so gewählt werden, dass wir für \(M_2\) ein gleich grosses Drehmoment, wie \(M_1\) erhalten, nur in der anderen Richtung. Damit wirken jetzt \(M_1\) und \(M_2\) und beide heben sich auf, so dass \(M_{res}=0\).
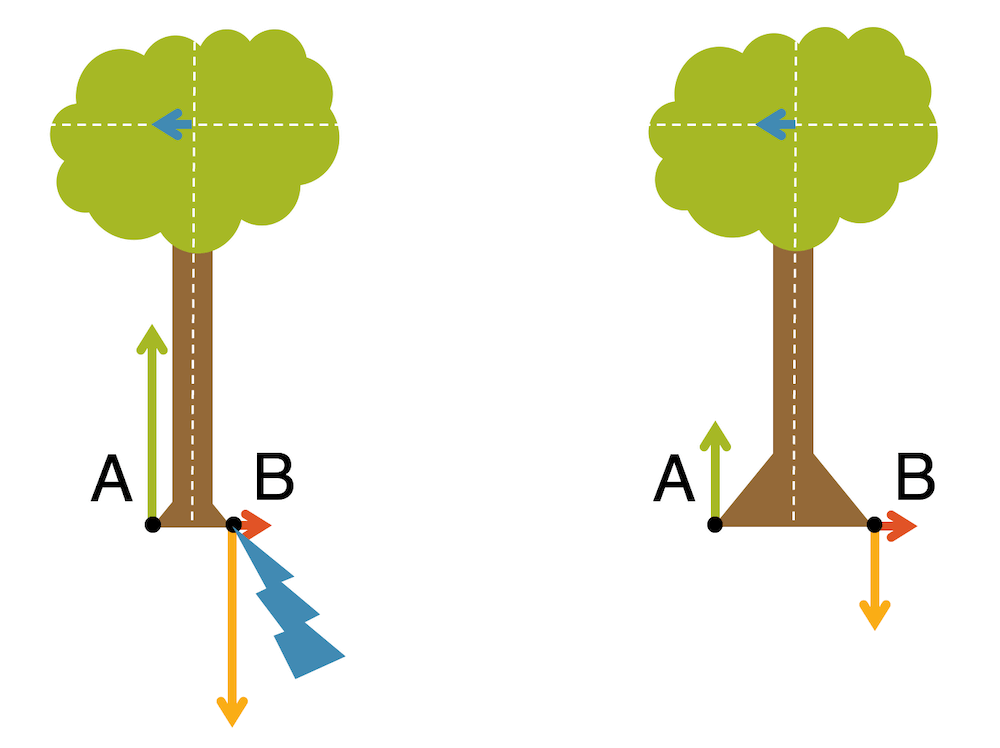
Ist der Baum jetzt stabil? Nein, er kippt zwar nicht mehr im Gegenuhrzeigersinn weg, aber er verschiebt sich nach links und in den Boden hinein! Warum das jetzt?
Wenn wir die resultierende Kraft in horizontaler Richtung betrachten, so wird die Windkraft \(F_4\) nicht aufgehoben. Wir hätten deshalb, gemäss Newtons Zweitem Gesetz eine Beschleunigung des Baums von rechts nach links. Deshalb führen wir jetzt \(F_3\) ein, das gleich gross aber entgegengesetzt sein soll, wie \(F_4\). Damit erhalten wir \(F_{res}=0\) in der horizontalen Richtung.
Das Gleiche tun wir in der vertikalen Richtung: Die Kraft \(F_2\) würde unseren Baum in den Boden versinken lassen, wenn sie weiterhin alleine da wäre. Mit der neuen Kraft \(F_1\) wird sie aber in der vertikalen Richtung aufgehoben, so dass wir jetzt auch hier Kräftegleichgewicht haben.
Zusammengefasst: Die Kraft des Winds \(F_4\) an der Krone hat zur Folge, dass an der Wurzel die Kräfte \(F_1\), \(F_2\) und \(F_3\) wirken. Nur so können wir sicherstellen, dass wir Kräfte- und Drehmomentgleichgewicht, d.h. \(F_{res}=0\) und \(M_{res}=0\) in allen Richtungen haben, was die Voraussetzung für ein stabiles, statisches System ist.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.