Reibungskraft

Modellvorstellung

Oberflächen sind meistens rau. Wenn zwei raue Oberflächen aneinander reiben, entsteht die Gleitreibung. Es braucht auch eine gewisse Kraft, um die beiden Oberflächen relativ zueinander zu bewegen. Mit der Zeit können die beiden Flächen warm werden.

Die Rauheit können wir uns als Unebenheit der Fläche vorstellen. Die “Zacken” oder “Berge” ragen heraus und kollidieren mit den “Zacken” bzw. “Bergen” der anderen Oberfläche. Ein Bewegen ist nur möglich, wenn die “Zacken” sich verformen und sich so schliesslich einander aus dem Weg gehen. Das Verformen von Material ist nur mit einer Kraft möglich. Bei dauerhafter Verformung wird sogar mechanische Arbeit in Wärme umgewandelt. Das nennt sich dann Reibungsarbeit.

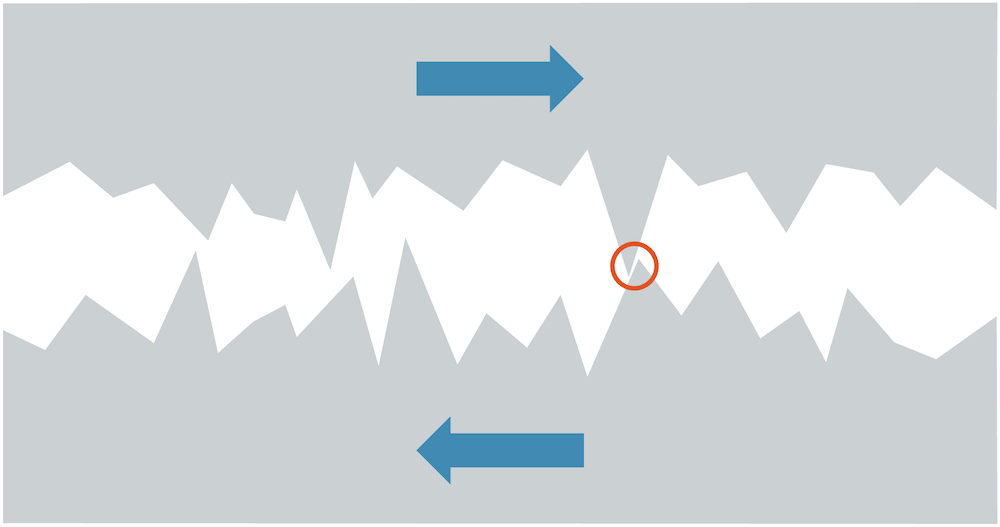
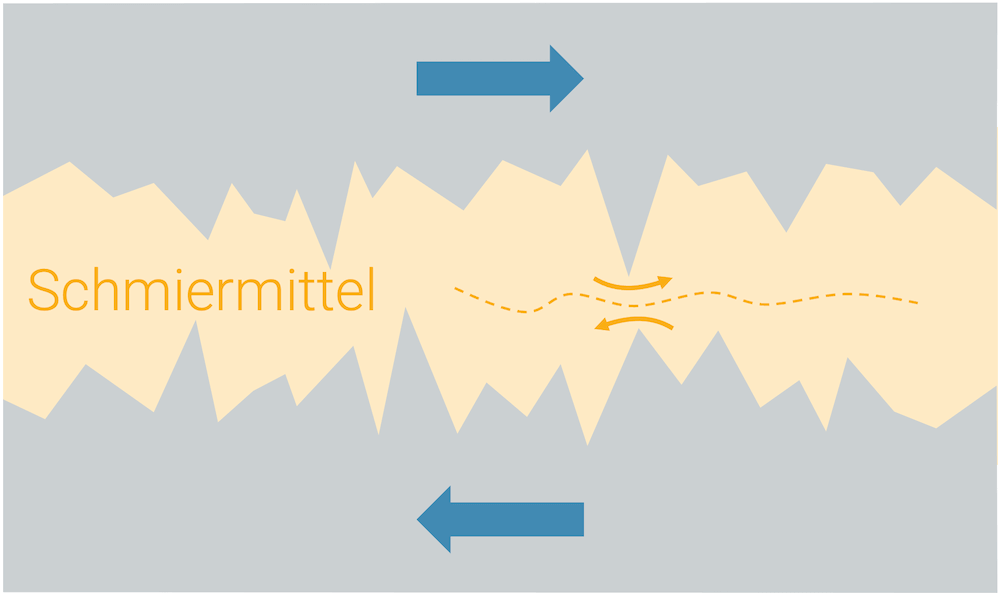
Wenn wir eine Flüssigkeit zwischen die beiden Oberflächen einbringen, kann sie den Abstand zwischen den “Zacken” erhöhen, so dass sie sich nicht mehr direkt im Wege stehen. Die Flüssigkeit kann fliessen und so den Zacken ausweichen.

Die beiden Flächen können sich jetzt viel leichter relativ zueinander bewegen. Eine solche Flüssigkeit nennen wir Schmierflüssigkeit. In Maschinen und Getrieben ist es Öl oder Fett.

Den gleichen Effekt erhalten wir aber auch bei nassen Strassen. Die Wasserschicht erzeugt einen Schmierfilm zwischen Reifen und Asphalt und reduziert dadurch die Gleitreibung. Beim sog. “Aquaplaning” rutscht ein Auto bei Vollbremsung viel weiter, als auf trockener Strasse.

Richtung der Reibungskraft

Wenn wir Möbel verschieben, braucht es manchmal ganz schön viel Kraft, bis sie sich endlich bewegen. Die Kraft, die sich einer Bewegung widersetzt oder auch die kleinste Bewegung sofort wieder stoppt, ist die Reibungskraft.

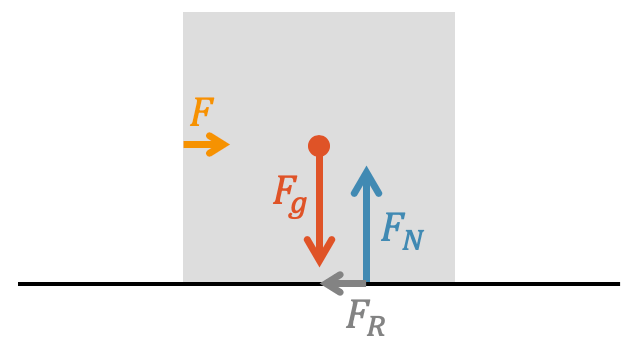
Wir drücken auf das Möbel mit der Kraft \(F\) (orange). Die Reibungskraft \(F_R\) (grau) wirkt immer der Bewegung entgegen. Das gilt auch im Fall der Haftreibungskraft.

Aus der obigen Grafik kann nicht erkannt werden, ob das Möbelstück sich schon in der Gleitreibung befindet (und sich nach rechts bewegt) oder ob es noch still steht und sich der Bewegung mit Hilfe der Haftreibung widersetzt.

Die Normalkraft wird von der Gewichtskraft kompensiert, so dass beide Kräfte sich aufheben. Sie haben aber nur scheinbar nichts mit der Reibung und der horizontalen Richtung zu tun. Es gibt nämlich, bei allen Formen der Reibungskraft, eine Abhängigkeit der Reibungskraft von der Normalkraft: Je stärker die beiden Flächen zusammengedrückt werden, desto grösser ist die Reibungskraft.

Ein schweres Möbelstück hat eine grössere Gewichtskraft \(F_g\) und damit auch eine grössere Normalkraft \(F_N\). Die Gleitreibungskraft ist proportional zur Normalkraft, d.h. das schwere Möbelstück erfährt eine grössere Reibungskraft und ist viel mühsamer zu bewegen, als ein leichtes Möbelstück.

Im nachfolgenden Beispiel ist die Gleitreibungskraft \(F_R\) gezeigt, die an der Klinge wirkt. Der Schleifstein dreht sich nach hinten und “möchte” das Metall mitziehen. Eine Person hält sie zurück, so dass das Stück Metall an Ort und Stelle bleibt.

Beachte: Aus Sicht des Schleifsteins ist die Reibungskraft gerade umgekehrt gerichtet und bremst die Drehrichtung nach hinten. Gemäss Newtons Drittem Gesetz haben wir ein Kräftepaar von einer Reibungskraft nach hinten, die auf das Metall wirkt und eine Reibungskraft nach vorne, die den Schleifstein bremst.

Ist Reibung gut oder schlecht?

Reibung ist in vielen Fällen unerwünscht, da wegen ihr ein Teil der eingesetzten Energie in unnütze Wärme umgewandelt wird. In diesen Fällen wird sie möglichst klein gehalten durch:

• Rollen statt Gleiten (Rollreibung ist günstiger als Gleitreibung)
• Verringerung der Normalkraft
• Reduktion des Reibungskoeffizienten (Materialwahl, Schmierung, Härte des Materials bei Rollreibung etc.)

In vielen Fällen ist Reibung erwünscht, z.B. brauchen wir Haftreibung für unsere Fortbewegung (Gehen, Fahren in Kurven) oder wir nutzen die Reibung für die Befestigung (Nagel, Schraube, Klemme). Sie lässt sich verstärken durch:

• Raues Material
• Noppen, Rillen z.B. auf einer rutschfreien Unterlage
• grössere Normalkraft (mehr Gewicht oder grössere Klemmkraft)

Gleitreibung

Bei der Gleitreibung reiben die beiden Flächen aufeinander. Sie bewegen sich relativ zueinander.

Beispiele:

• Die Fläche der Skier reibt auf dem Schnee
• Wir reiben unsere Hände, um sie aufzuwärmen
• Die Bremsen reiben an der Bremsscheibe etc.

Die Gleitreibungskraft ist proportional zur Normalkraft:

\[ F_{GR} = \mu_G \cdot F_N \]

Verdoppeln wir die Normalkraft, d.h. drücken wir mit einer grösseren Kraft die beiden Flächen zusammen, so verdoppelt sich auch die Gleitreibungskraft.

Der Gleitreibungskoeffizient \(\mu_G\) kann aus Tabellen abgelesen werden. Er berücksichtigt die Beschaffenheit der beiden Oberflächen:

• Glatte, gut gleitende Oberflächen: \(\mu_G\) klein (z.B. Geschmierter Stahl auf Stahl: \(\mu_G=0.011\))
• Raue Oberflächen: \(\mu_G\) gross (z.B. Gummi auf Asphalt: \(\mu_G=0.51\))

Rollreibung

Rollreibung entsteht, wenn Räder auf dem Boden, der Strasse oder den Schienen abrollen. Beim Abrollen drücken sie kurzzeitig auf die Oberfläche, gleiten aber nicht auf ihr. Es handelt sich deshalb nicht um Gleitreibung.

Die Reibung entsteht im Material der Räder und der Unterlage. Deren Materialien werden elastisch zusammengedrückt und danach wieder entspannt. Bei diesem Prozess entsteht innere Reibung im Material, bei welcher ein Teil der Energie in Wärme umgewandelt wird.

Harte Materialien verformen sich wenig und erzeugen deshalb wenig Rollreibung (z.B. gehärtete Stahlkugeln in Kugellagern). Besonders weiche Materialien haben mehr Rollreibung und erwärmen sich durch die Energieumwandlung (z.B. Gummireifen mit wenig Luftdruck)

Beispiele:

• Reifen auf Asphalt
• Gehärtete Stahlkugeln im Kugellager (extrem kleine Rollreibung)
• Rollen eines Golfballs auf dem Rasen

Die Rollreibungskraft ist proportional zur Normalkraft:

\[ F_{RR} = \mu_R \cdot F_N \]

Eine Erhöhung der Normalkraft verstärkt die Verformung im Innern des abwälzenden Teils und auch der Unterlage und verstärkt damit die Rollreibung.

Der Rollreibungskoeffizient \(\mu_R\) kann aus Tabellen abgelesen werden. Er berücksichtigt die innere Reibung der beiden Materialien (Wälzkörper und Unterlage) aufgrund der abwechselnden Kompression/Entspannung:

• Harte Materialien: \(\mu_R\) klein (z.B. Gehärtete Stahlkugeln auf Stahl: \(\mu_R=0.0013\))
• Weiche Materialien: \(\mu_R\) gross (z.B. Gummireifen auf weichem Untergrund, z.B. Sand: \(\mu_R=0.33\))

Im Vergleich zu anderen Reibungskoeffizienten ist der Rollreibungskoeffizient um Grössenordnungen kleiner als der Gleit- oder Haftreibungskoeffizient! Rollen ist viel effizienter als Gleiten – deshalb haben wir Menschen das Rad erfunden! 🙂

Haftreibung

Wenn wir weder ein Gleiten, noch ein Rollen haben und die beiden Flächen gewissermassen “zusammenhaften”, haben wir Haftreibung.

Im obigen Bild rutscht der Mann von der Palme nicht ab, weil er mit den Händen und Füssen gegen sie drückt. Wäre die Palme extrem glatt, d.h. wäre der Haftreibungskoeffizient \(\mu_H\) sehr klein, könnte er die Palme nicht hochklettern.

Beispiele:

• Wir halten einen Stift zwischen zwei Fingern
• Haftung mit dem Boden, wenn wir gehen
• Ein Kiste steht auf einer schrägen Rampe, rutscht aber nicht ab

Die Haftreibungskraft ist nicht proportional zur Normalkraft! Das ist der grosse Unterschied zu den anderen Reibungskräften! Sie nimmt genau den Betrag ein, den es für ein Kräftegleichgewicht braucht, gemäss Newtons Drittem Gesetz (Wechselwirkungsgesetz). Sie passt sich der Situation an.

Die Haftreibungskraft hat eine Obergrenze, die maximal mögliche Haftreibungskraft \(F_{HRmax}\) und diese berechnet sich, abhängig von der Normalkraft.

\[ F_{HRmax} = \mu_H \cdot F_N \]

Überschreitet die Haftreibung diese Obergrenze, so stellt sich Gleitreibung ein.

Wenn unser Mann an der Palme sich zu wenig stark an der Palme klammert, verringert er die Normalkraft, was zu einem Absenken der Obergrenze führt. Er riskiert dann, dass er die Haftreibungskraft, die seiner Gewichtskraft entspricht, diese Obergrenze überschreitet und er abrutscht.

Der Haftreibungskoeffizient \(\mu_H\) kann aus Tabellen abgelesen werden. Er berücksichtigt die Beschaffenheit der beiden Oberflächen. Er ist im Normalfall grösser als der Gleitreibungskoeffizient:

• Glatte, gut gleitende Oberflächen: \(\mu_H\) klein (z.B. Teflon auf Teflon: \(\mu_H=0.042\))
• Raue Oberflächen: \(\mu_H\) gross (z.B. Gummi auf trockener Betonoberfläche: \(\mu_H=1.02\))