Haftreibung

Die Haftreibung ist, neben der Gleitreibung und Rollreibung, eine der drei Formen der Reibungskraft. Die beiden Flächen berühren sich und “haften” gewissermassen zusammen. Bei der Haftreibung reiben die zwei Flächen nicht aufeinander, d.h. sie bewegen sich nicht relativ zueinander.

Weil diese Oberflächen nicht ganz glatt sind und zusammen “haften”, entsteht eine Reaktionskraft, sobald von aussen Kräfte wirken, die versuchen, die beiden Oberflächen zum Bewegen zu bringen. Die Haftreibungskraft ist einer möglichen Bewegung entgegengesetzt.

Beispiele für Haftreibung:

• Die Haftreibung zwischen unseren Schuhsohlen und dem Boden ermöglicht ein sicheres, rutschfreies Gehen und Laufen
• Die Haftreibung zwischen den Autoreifen und der Strasse sorgt dafür, dass das Auto sicher beschleunigen, bremsen und Kurven fahren kann.
• Beim Klettern verhindert die Haftreibung zwischen den Händen/Füßen und der Kletterwand ein Abrutschen
• Beim Schreiben hilft die Haftreibung zwischen Stiftspitze und Papier, dass wir nicht immer gleich abrutschen.
• Die Haftreibung zwischen den Stuhlbeinen und dem Boden verhindert, dass der Stuhl leicht verrutscht, wenn wir uns auf ihn setzen.

Die Haftreibung ist grösser als die Gleitreibung und damit automatisch auch grösser als die Rollreibung.

Meistens ist die Haftreibung gewollt. Wenn sie aber ungewollt ist und nicht verhindert werden kann, empfiehlt sich die Wahl von gut gleitenden Materialien (z.B. Teflon) oder der Einsatz von Schmiermitteln. Vielleicht kann die Normalkraft reduziert werden, was direkt zu einer Reduktion der Haftreibungskraft führt.

Das Motorrad in der Kurve rutscht nicht weg, dank der Haftreibungskraft zwischen Reifen und Asphalt. Seitlich gesehen, bewegt sich das Motorrad nicht. Es ist Haftreibung.

Bei nasser Strasse wirkt der Wasserfilm wie ein Schmiermittel, der den Haftreibungskoeffizienten signifikant reduziert. Damit senkt das Wasser die Obergrenze der Haftreibung, so dass Fahrzeuge viel schneller die Haftreibung verlassen und ins Schleudern (Gleitreibung) kommen. Um das sog. ‘Aqua Planing’ zu verhindern, sollte bei nassen Verhältnissen die Geschwindigkeit angepasst werden.

Wenn wir einen Nagel einschlagen, hält er anschliessend nur dank Haftreibungskraft. Da das elastische Holz gegen den Nagel drückt, wird eine relativ grosse Obergrenze für diese Haftreibung erreicht. Sie kann nur mit Hilfe einer Beisszange und mit Hilfe von Hebelkräften überwunden werden.

Abhängigkeit von der Normalkraft

Wenn wir die Haftreibung berechnen möchten, ist das etwas komplizierter als bei der Gleitreibung oder Rollreibung, denn die Haftreibungskraft ist nicht proportional zur Normalkraft.

Die Haftreibungkraft folgt aus der Kräftesituation und stellt sich gemäss Newtons Drittes Gesetz so ein, dass Kräftegleichgewicht herrscht.

Es gibt für die Haftreibung aber eine Obergrenze, bis zu welcher die beiden Oberflächen aneinander haften können. Darüber lässt die Haftung los und wir kriegen ein Gleiten.

Diese Obergrenze, d.h. die maximal mögliche Haftreibungskraft \(F_{HRmax}\) können wir bestimmen. Sie ist proportional zur Normalkraft:

\[ F_{Rmax} = \mu_H \cdot F_N \]

Der Proportionalitätsfaktor ist der Haftreibungskoeffizient \(\mu_H\). Je kleiner der Haftreibungskoeffizient, desto tiefer liegt die Obergrenze bei einer gegebenen Normalkraft:

Wir bestimmen dann die Reibungskraft, die wir haben möchten, damit Kräftegleichgewicht herrscht, d.h. keine Beschleunigung stattfindet. Wir verlangen Kräftegleichgewicht (\(F_{res}=0\). Wenn die dazu benötigte Haftreibungskraft kleiner als die maximal mögliche Obergrenze \(F_{Rmax}\) ist, wird Haftreibung möglich sein.

Falls die Obergrenze aber überschritten wird, kann keine so grosse Haftreibungskraft aufgebracht werden. Es entsteht dann meistens Gleitreibung, d.h. wir müssen die Berechnung wieder von vorne beginnen – dieses Mal für die Gleitreibung.

Beispiel

Das Vorderrad eines Autos \((m=1.8\,\text{t})\) überträgt einen Viertel der Gewichtskraft. Es dreht im Schnee durch. Die Gleitreibungskraft beträgt \(F_{GR} = 662\,\text{N}\). Wie viel beträgt die Haftreibungskraft? (Haftreibungskoeffizient: \(\mu_H=0.25\)) Wie ist die Haftreibungskraft am Auto gerichtet? (gegeben ist die Gleitreibungskraft \(F_{GR}\) vorne)

Lösung

Das Vorderrad versucht ja, das Auto nach vorne zu bewegen. Allerdings ist diese Kraft zu schwach, d.h. eine Haftreibungskraft widersetzt sich der Bewegung und zeigt deshalb nach hinten. Sie greift an der Stelle an, wo das Auto mit dem Boden Kontakt hat, also am Hinterrad.

Da für das Auto Kräftegleichgewicht gilt (es ist in Ruhe und bleibt in Ruhe), gilt \(F_{res}=0\) oder \(F_R = F_{GR}\). Die Haftreibungskraft stellt sich genau so ein, dass Kräftegleichgewicht herrscht. Die bremsende Haftreibungskraft ist deshalb genau gleich gross, wie die beschleunigende Gleitreibungskraft am Vorderrad: \[ \underline{F_R = 662\,\text{N}} \] Wir untersuchen jetzt, ob die Haftreibungskraft unterhalb ihrer Grenze ist. Diese ist abhängig von der Normalkraft. \[ F_N = F_g = m \cdot g = 1’800\,\text{kg} \cdot 9.81\,\frac{\text{m}}{\text{s}^2} \] \[ F_N = 17’658\,\text{N} \] \[ F_{R,max} = \mu_H \cdot F_N = 0.25 \cdot 17’658\,\text{N} = 4’415\,\text{N} \] Die Obergrenze ist nicht überschritten, d.h. das Hinterrad (bzw. beide Hinterräder) haben genug Haftung mit dem Boden: \[ F_R = 662\,\text{N} < 4’415\,\text{N} \]

Beispiel

Im Film Divergent (2014) rettet Tris die fallende Kristina. Zeichne die fehlenden Kräfte für Kristina (links) und für Tris (rechts) ein, unter der Annahme, dass beide gleich schwer sind und Haftreibungskoeffizient \(\mu_H>0.5\).

Lösung

Die fallende Kristina wird zurückgehalten, d.h. sie muss im Kräftegleichgewicht sein. Die Kraft, mit welcher Tris sie zurückhält entspricht ihrer Gewichtskraft: \[ F_{R1} = F_g \] Beide Kräfte heben sich auf und wir haben Kräftegleichgewicht \((F_{res} = 0)\), d.h. Kristina wird nicht mehr nach unten mit \(g\) beschleunigt.

Bei Tris ist die Situation etwas komplizierter. Sie hat die gleiche Kraft \(F_{R1}\), mit welcher sie Kristina zurückhält. Für Tris ist das aber eine Kraft, die nach unten zeigt. Es ist ja letztlich die Gewichtskraft von Kristina.
Jetzt wirkt der Boden zweifach gegen diese Kräfte nach unten: Tris’ Gewichtskraft wird vom Boden aufgenommen mit einer Normalkraft \(F_{N1}\) und Kristinas Gewichtskraft wird von der Normalkraft \(F_{N2}\) aufgenommen.
Diese zeigt aber etwas schräg nach vorne und Kristina muss den Anteil nach vorne mit der Haftreibungskraft \(F_{R2}\) nach hinten kompensieren, sonst rutscht sie nach vorne.

Erlaubt die Unterlage eine solche Haftreibungskraft? Wenn wir genau schauen, so ist \(F_{R2}\) etwas halb so stark, wie \(F_{N1}\). Für die Obergrenze der Haftreibung gilt aber: \[ F_{H,max} = \mu_H \cdot F_{N1} = 0.25 \cdot F_{N1} \] Die Obergrenze liegt bei einem Viertel der Normalkraft und die Reibungskraft, die Tris bräuchte ist aber rund doppelt so gross! Tris wird deshalb nicht haften bleiben, sondern durch das Gewicht von Kristina nach vorne rutschen. Sorry, Filmfehler! 😉

Haftreibung an der schiefen Ebene

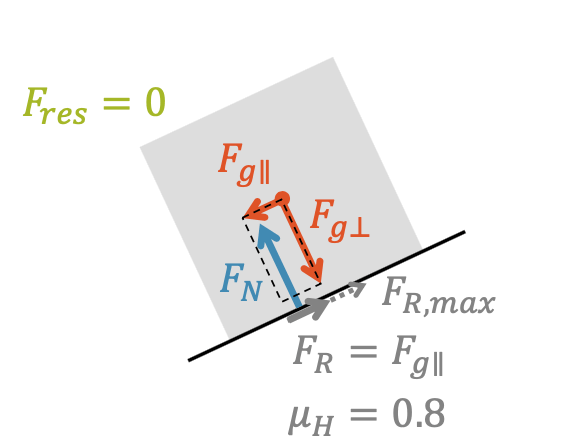
Die Haftreibung \(F_R\) ist gerade so gross, dass sie die Parallelkomponente der Gewichtskraft \(F_{g \parallel}\) aufhebt und wir in paralleler Richtung zur Ebene ein Kräftegleichgewicht erhalten. Senkrecht zur Ebene haben wir bereits Kräftegleichgewicht, da die Normalkraft \(F_N\) die Senkrechtkomponente der Gewichtskraft \(F_{g \perp}\) kompensiert.

Sollten wir die \(F_{R,max}\) überschritten haben oder wurde der Klotz leicht bewegt, so fällt die Haftreibungskraft weg und wir wechseln zur Gleitreibung. Da der Gleitreibungskoeffizient aber kleiner ist als der Haftreibungskoeffizient (\(\mu_G < \mu_H\)), ist die Reibungskraft nicht mehr in der Lage das Kräftegleichgewicht zu halten. Die resultierende Kraft beschleunigt dann den Klotz den Hang hinunter.

Wir können dieses theoretisch anmutende Beispiel direkt mit dem Abstellen eines Autos an einer steilen Strasse vergleichen: Die Haftreibung zwischen den Reifen und dem Boden verhindert, dass das Auto wegrutscht.

Wäre die Strasse noch steiler, könnte eventuell die Obergrenze der Haftreibung erreicht werden. In so einem Fall müsste man einen Keil unter das Rad anbringen, um mit der zusätzlichen Normalkraft die zu grosse Parallelkomponente der Gewichtskraft \(F_{g \parallel}\) zu kompensieren.