
Image by Michael Pechardo, shared on Unsplash
Die Haftreibung ist, neben der Gleit- und Rollreibung, eine der drei Formen der Reibungskraft. Bei der Haftreibung reiben zwei Flächen nicht gegen einander, denn sie bleiben zusammen, als würden sie haften. Die Haftreibungskraft \(F_R\) ist, ähnlich wie die Normalkraft, eine Reaktionskraft, die sich an die äussere Aktionskraft anpasst (Newton 3). Sie wird deshalb immer nur so gross sein, wie es das Haften der beiden Oberflächen erfordert.
Die Haftreibung kann aber eine gewisse Obergrenze \(F_{R,max}\) nicht überschreiten. Diese maximale Haftreibungskraft ist abhängig von der Normalkraft und vom Haftreibungskoeffizienten \(\mu_H\), der von Material und Oberflächenbeschaffenheit abhängt:
\[ F_R \leq F_{R,max} \quad \quad \quad F_{R,max} = \mu_H \cdot F_N \]
Wenn wir weder ein Gleiten, noch ein Rollen haben und die beiden Flächen gewissermassen “zusammenhaften”, sich also zusammen gleich bewegen oder sogar in Ruhe bleiben, dann haben wir Haftreibung. Beispiel: Wenn wir einen Stift zwischen zwei Fingern halten, so verhindert die Haftreibung, dass er fallen kann. Auch die Haftreibung ist abhängig von der Normalkraft, denn wenn wir den Druck der Finger lockern, gleitet uns der Stift irgendwann aus den Fingern. Im Gegensatz dazu erfährt ein eingeschlagener Nagel eine so grosse Normalkraft rundherum, dass wir ihn nur mit einer Zange und viel Kraft herausziehen können.
Beispiele für Haftreibung:
- Abstossbewegung des Fusses beim Gehen
- Abrollen des Rads auf der Strasse (statt Durchdrehen)
- Hängenbleiben von Schnee auf einem Giebeldach
- Nagel oder Schraube in einem weichen Material (z.B. Holz)
- Türkeil oder Keil, der ein Auto daran hindert weg zu rollen
Wenn wir die Haftreibung berechnen möchten, ist das etwas komplizierter als bei der Gleitreibung oder Rollreibung. Zuerst müssen wir die Obergrenze der Haftreibung bestimmen. Sie ist proportional zur Normalkraft. Der Proportionalitätsfaktor heisst Haftreibungskoeffizient \(\mu_H\). Je kleiner der Haftreibungskoeffizient, desto tiefer liegt die Obergrenze bei einer gegebenen Normalkraft:
\[ F_{R,max} = \mu_H \cdot F_N \]
Nun bestimmen wir die Reibungskraft, die wir haben möchten, damit keine Beschleunigung stattfindet. Wir verlangen also Kräftegleichgewicht bzw. dass die resultierende Kraft null ist: \(F_{res}=0\). Wenn die dazu benötigte Haftreibungskraft kleiner als die maximal mögliche Obergrenze \(F_{R,max}\) ist, dann haben wir die Haftreibungskraft damit bestimmt.
Falls ie Obergrenze aber überschritten wird, kann keine so grosse Haftreibungskraft aufgebracht werden und es entsteht dann meistens Gleitreibung, d.h. wir müssen die Berechnung wieder von vorne beginnen – dieses Mal für die Gleitreibung.
Haftreibung an der schiefen Ebene
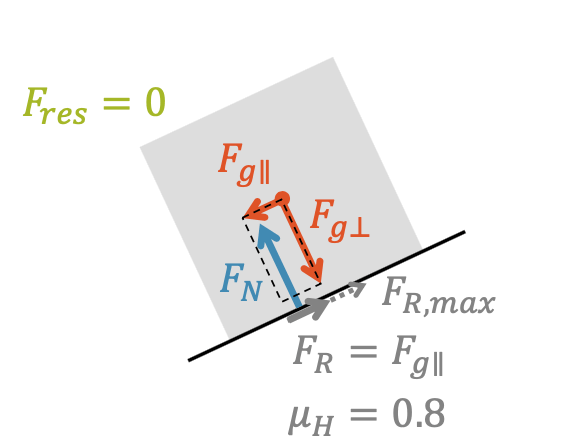
Die Haftreibung \(F_R\) ist gerade so gross, dass sie die Parallelkomponente der Gewichtskraft \(F_{g \parallel}\) aufhebt und wir in paralleler Richtung zur Ebene ein Kräftegleichgewicht erhalten. Senkrecht zur Ebene haben wir bereits Kräftegleichgewicht, da die Normalkraft \(F_N\) die Senkrechtkomponente der Gewichtskraft \(F_{g \perp}\) kompensiert.
Sollten wir die \(F_{R,max}\) überschritten haben oder wurde der Klotz leicht bewegt, so fällt die Haftreibungskraft weg und wir wechseln zur Gleitreibung. Da der Gleitreibungskoeffizient aber kleiner ist als der Haftreibungskoeffizient (\(\mu_G < \mu_H\)), ist die Reibungskraft nicht mehr in der Lage das Kräftegleichgewicht zu halten. Die resultierende Kraft beschleunigt dann den Klotz den Hang hinunter.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.