Die Integralrechnung wird in der Physik sehr viel gebraucht. Eine typische Anwendung ist für die Berechnung der physikalischen Arbeit von sich verändernden Kräften. Wir beginnen mit einem sehr einfachen Beispiel, das noch ohne Integral auskommen würde, werden daran aber erkennen, wie nützlich die Integralrechnung für etwas kompliziertere Fälle wird.
Wir schauen uns zuerst das Beispiel der Hubarbeit an. Hier wird eine Masse angehoben. Physikalische Arbeit ist definiert als Kraft mal Weg. Die Kraft ist die Gewichtskraft und der Weg ist die Höhe, über welche die Masse angehoben wird. Wir bezeichnen die Höhe im weiteren mit der allgemeineren Abkürzung \(s\) für die Wegstrecke:
\[ W = F_g \cdot s \]
Wenn wir aber nur ein ganz kleines bisschen anheben würden, nämlich gerademal \(dx\), dann braucht es dazu ein kleines bisschen Arbeit \(dW\):
\[ dW = F(x) \; dx \]
Mit dem Integral über die ganze Strecke erhalten wir die Summe aller kleinen Beiträge \(dW\) zur Gesamtarbeit \(W\):
\[ W = \int dW = \int_0^s F(x)\;dx \]
Die Kraft \(F(x)\) ist im Fall der Hubarbeit immer die Gewichtskraft \(F_g\) und die ist konstant. Im Integral eingesetzt, kann sie als konstanter Faktor mit der Faktorregel aus dem Integral ausgeklammert werden:
\[ W = \int_0^s F_g\;dx = F_g \cdot \int_0^s dx \]
\[ = F_g \cdot \Big[ x \Big]_0^s = F_g \cdot (s-0) \]
\[ = \underline{F_g \cdot s} \]
Et voilà: Wir haben Kraft mal Weg, wie erwartet. Das Integral war hier nicht wirklich nötig, weil die Kraft konstant war. Wenn sie aber eine Funktion von \(x\) ist, dann kann die Arbeit nur mit einem Integral gelöst werden.
Als nächstes schauen wir uns deshalb eine Federkraft an. Sie ist definitiv nicht konstant. Eine Feder erzeugt, gemäss dem Hooke’schen Gesetz, eine umso grössere Kraft, je stärker die Feder auseinander gezogen oder zusammen gedrückt ist. Mit \(k\) wird die Federkonstante bezeichnet:
\[ F(x) = k \cdot x \]
Wir berechnen die Spannarbeit an der Feder wieder wie im Beispiel der Hubarbeit:
\[ W = \int dW = \int_0^s F(x)\;dx = \int_0^s k \cdot x\;dx \]
\[ = k \cdot \Big[ \frac{1}{2} x^2 \Big]_0^s \]
\[ = \frac{1}{2} k \cdot (s^2-0^2) \]
\[ = \underline{\frac{1}{2}ks^2} \]
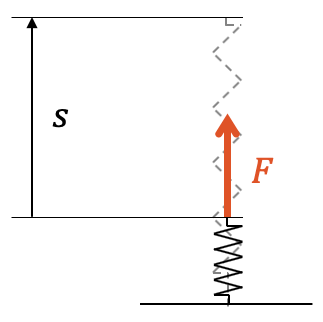
Damit haben wir die Spannarbeit an einer Hooke’schen Feder hergeleitet.
Berechnung der physikalischen Arbeit als Integral vieler kleiner Beiträge von Arbeit \(dW\) als Produkt der ortsabhängigen Kraft \(F(x)\) und einer infinitesimaler Wegstrecke \(dx\):
\[ dW = F(x)\;dx \]
\[ W = \int dW \]
Beispiel
Berechne die Arbeit, die es braucht, um sich aus dem Gravitationsfeld der Erde zu befreien. Die Gravitationskraft ist mit Newtons Gravitationsgesetz gegeben:
\[ F(x) = G \cdot \frac{Mm}{(x+r_E)^2} \]
\(G\) ist die Gravitationskonstante, \(M\) die Masse der Erde und \(m\) die Masse, die im Gravitationsfeld angehoben wird. Der Abstand der beiden Schwerpunkte ist \((x+r_E)\), wobei \(r_E\) der Radius der Erde ist und \(x\) die Höhe oberhalb der Erdoberfläche.
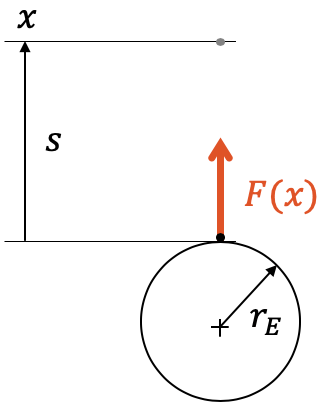
Wir stellen wieder die Gleichung für die physikalische Arbeit auf und setzen für \(F(x)\) die Gravitationskraft ein. In einem ersten Schritt nehmen wir einfach an, dass wir über eine allgemeine Wegstrecke \(s\) anheben:
\[ W = \int dW = \int_0^s F(x)\;dx \]
\[ = \int_0^s G \cdot \frac{Mm}{(x+r_E)^2}\;dx \]
\[ = GMm \int_0^s \frac{1}{(x+r_E)^2}\;dx \]
Um das Integral zu lösen, machen wir eine Substitution: \(u=(x+r_E)\) und so \(du=dx\). Für die Integrationsgrenzen erhalten wir \(r_E\) und \(s+r_E\):
\[ W = GMm \int_{r_E}^{s+r_E} \frac{1}{u^2}\;du \]
\[ = GMm \cdot \Big[ -\frac{1}{u} \Big]_{r_E}^{s+r_E} \]
\[ = GMm \cdot \Big( -\frac{1}{s+r_E} + \frac{1}{r_E} \Big) \]
\[ = GMm \cdot \Big( \frac{1}{r_E} -\frac{1}{s+r_E} \Big) \]
Das Gravitationsfeld der Erde wird mit zunehmendem Abstand immer schwächer. Rein theoretisch verschwindet die Gravitationskraft aber nie vollständig, erst in unendlichem Abstand. Die Arbeit, die benötigt ist, um sich vollständig aus dem Gravitationsfeld der Erde zu befreien ist somit der Grenzwert für \(s \rightarrow \infty\):
\[ \require{cancel} W_{\infty} = \lim_{s \rightarrow \infty} \Big( GMm \cdot \big( \frac{1}{r_E} -\cancel{\frac{1}{s+r_E}} \big) \Big) \]
\[ = \underline{\frac{GMm}{r_E}} \]
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.