Die Übertragung der elektrischen Arbeit vom Kraftwerk bis zum Verbraucher wäre ohne Hochspannung nicht denkbar und die Hochspannung ist nur mit Transformatoren zu erreichen. In der nachfolgenden Grafik sehen wir die Verbindung des Verbrauchers (rechts) mit dem Kraftwerk (links). Wir haben hier mindestens drei Transformatoren: Zuerst wird die Spannung aus dem Kraftwerk auf Hochspannung gebracht. Mit Hochspannung werden die grossen Distanzen überwunden und dann wird diese Spannung in zwei Schritten heruntertransformiert: Für die regionale Verteilung wird auf Mittelspannung runter-transformiert und schliesslich für die Verbraucher auf Niederspannung von 230 V gebracht.
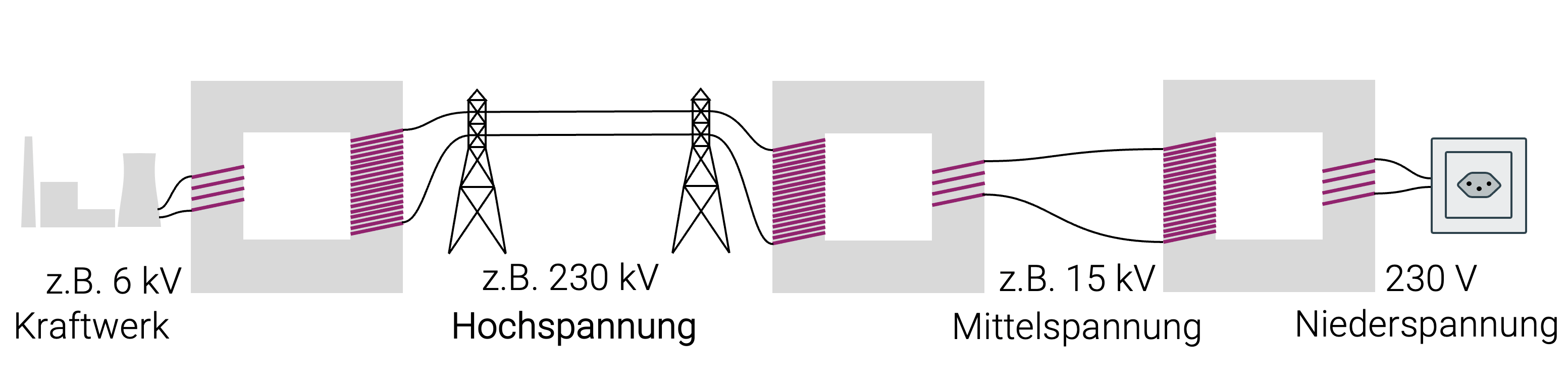
Weniger Übertragungsverluste dank Hochspannung
Die Hochspannung wird eingesetzt, um die Verluste bei der Übertragung niedrig zu halten. Um dies zu verstehen, betrachten wir zuerst die Übertragung ohne Hochspannung. Die Verluste entstehen durch den elektrischen Widerstand der Übertragungsleitung. Gemäss dem ohm’schen Gesetz fällt über der gesamten Leitung mit dem Gesamtwiderstand \(R_L\) eine Spannung \(U_L\) ab:
\[ U_L = R_L \cdot I \]
Da wir im Stromkreis einen Hinweg und einen Rückweg haben, fällt die Spannung \(U_L\) zweifach ab. Wenn wir Kirchhoffs Zweites Gesetz, die Maschenregel, anwenden, sehen wir, dass die ursprüngliche Spannung \(U\) der Spannungsquelle (Kraftwerk) nur noch mit \(U-2U_L\) beim Verbraucher ankommt.
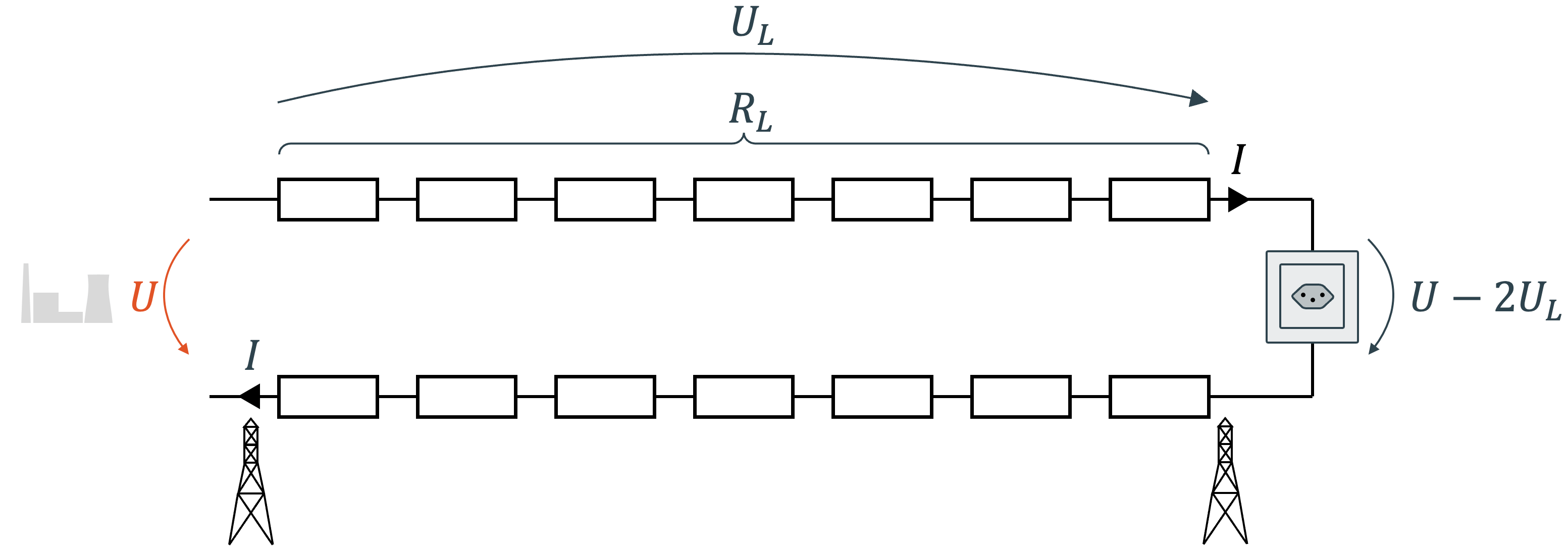
Wie viel elektrische Leistung verlieren wir hier über die Leitung? Die Verlustleistung \(P_V\) ist die Energie pro Zeit, die im Leitungs-Gesamtwiderstand in Wärme umgewandelt wird. Sie berechnet sich aus dem Produkt von Spannung und Strom:
\[ P_V = U_L \cdot I \]
Die Spannung \(U_L\) können wir mit dem ohm’schen Gesetz auch ersetzen mit \(U_L = R_L \cdot I\) und erhalten so:
\[ P_V = (R_L \cdot I) \cdot I = R_L \cdot I^2 \]
Wir sehen jetzt, dass die Verlustleistung von zwei Faktoren abhängt: dem Leitungswiderstand \(R_L\) und dem Strom \(I\). Um die Verlustleistung möglichst klein zu halten, brauchen wir einen möglichst kleinen Leitungswiderstand oder einen möglichst kleinen Strom oder am besten beides zusammen.
Der Leitungswiderstand kann mit der Wahl eines gut leitenden Materials reduziert werden. Allerdings spielen hier noch andere Betrachtungen eine Rolle: Das Material darf nicht zu schwer sein, weil die Leitungen zwischen den Strommasten hängen soll und durch das eigene Gewicht belastet wird. Das Material darf auch nicht zu teuer sein, weil viele Tausende von Kilometern an Leitungen verlegt werden müssen. Heutzutage wird deshalb Aluminium verwendet. Dieses Metall leitet zwar schlechter als Kupfer, ist dafür aber viel billiger und vor allem viel leichter.
Mit der Wahl von Aluminium haben wir einen Leitungswiderstand \(R_L\) gegeben, den wir nicht weiter senken können. Deshalb müssen wir den Strom möglichst tief halten. Es ist natürlich logisch, dass wir weniger Verluste haben, wenn wir weniger elektrische Arbeit übertragen – nur das ist sinnlos. Die Frage ist vielmehr: Wie können wir den Strom tief halten und trotzdem elektrische Arbeit übertragen?
Die Lösung zur Reduktion des Stroms liegt bei der Hochspannung: Wir erinnern uns dazu, dass die elektrische Spannung die Energie pro Ladung ist, d.h. die Menge an Energie, die letztlich jedes Elektron mit sich trägt. Bei einer hohen Spannung trägt ein Elektron viel Energie mit sich.
\[ \mathrm{Volt} = \frac{\mathrm{Joule}}{\mathrm{Coulomb}} \]
Der elektrische Strom ist die Menge an Ladung pro Zeit, d.h. wenig Strom bedeutet wenige Elektronen, die pro Zeit vorbeifliessen.
\[ \mathrm{Ampère} = \frac{\mathrm{Coulomb}}{\mathrm{Sekunde}} \]
Betrachten dazu eine Analogie im Verkehr: Wenn wir viele Personen von der einen Stadt in die andere Stadt bringen möchten, können wir dies mit wenig Spannung (nur eine Person pro Fahrzeug) und dafür viel Strom (viele Fahrzeuge, die pro Zeit vorbeifahren) erreichen. Die bessere Variante wäre dann aber mit viel Spannung (viele Personen pro Fahrzeug) und dafür wenig Strom (wenige Fahrzeuge pro Zeit). Deshalb wird die elektrische Arbeit mit einer möglichst hohen Spannung (viele Joules pro Coulomb) übertragen und damit der elektrische Strom (Coulomb pro Zeit) klein gehalten.
Wenn wir jetzt statt 230 V die tausendfache Spannung 230 kV benutzen, können wir mit einem ebenfalls tausendfach kleineren Strom \(I\) die gleiche Menge an elektrischer Arbeit übertragen. Durch den tausendfach kleineren Strom \(I\) wird das Quadrat davon (\(I^2\)) millionenfach kleiner. Die Verlustleistung ist bei gleichem Leitungswiderstand \(R_L\) dadurch millionenfach reduziert worden!
\[ P_V = R_L \cdot I^2 \]
Für die Stromübertragung über längere Distanzen werden Leitungen aus Aluminium eingesetzt, weil sie den elektrischen Strom gut leiten und Aluminium als Werkstoff günstig und leicht ist. Der Leitungswiderstand \(R_L\) führt zu einer Verlustleistung \(P_V\), die durch einen sehr kleinen Strom \(I\) tief gehalten wird. Dank Hochspannung kann trotz kleinem Strom immer noch viel elektrische Arbeit übertragen werden.
Die Hochspannung wird mit Hilfe von Transformatoren erreicht. Für die Grob- und Feinverteilung der elektrischen Arbeit zu den Verbrauchern wird die unpraktische und gefährliche Hochspannung stufenweise mittels Transformatoren heruntertransformiert.

Image by dimitrisvetsikas1969

Image by Silberfuchs
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.