
Der nach dem englischen Physiker John Henry Poynting (1852-1914) benannte Poynting-Vektor ist ein Vektor, der den Fluss der Energie im elektromagnetischen Feld beschreibt. Wir werden hier nicht nur erfahren, wie der Poynting-Vektor berechnet wird und welche Bedeutung er hat, sondern auch ganz Erstaunliches zum Transport von Energie erfahren.
Der Poynting-Vektor \(\vec{S}\) beschreibt die Richtung und den Betrag des Energieflusses pro Zeit und Fläche, d.h. es handelt sich um eine Intensität mit Richtung. Er wird berechnet durch das Vektorprodukt des E-Felds \(\vec{E}\) und des B-Felds \(\vec{B}\):
\[ \vec{S} = \frac{1}{\mu_0} \cdot \vec{E} \times \vec{B} \]
Dabei ist \(\mu_0\) die magnetische Permeabilität des Vakuums (physikalische Konstante):
\[ \mu_0 = 4 \pi \cdot 10^{-7} \, \frac{\text{N}}{\text{A}^2} \]
Energietransport im elektromagnetischen Feld
Im folgenden Bild siehst du ein Experiment, das im Klassenzimmer nur schwer vorzuzeigen ist: Eine Leuchtstoffröhre leuchtet. Sie tut das jedoch ohne Kabel – einfach so! Die Energie bezieht sie aus dem elektromagnetischen Feld, das sie umgibt. Unter einer Hochspannungsleitung ist dieses elektromagnetische Feld so stark, dass es eine solche Leuchtstoffröhre mit genügend Energie versorgt werden kann!
Das Geheimnis hinter diesem Experiment ist das gleichzeitige Auftreten von einem elektrischen Feld (E-Feld) und einem magnetischen Feld (B-Feld).

Image by BaronAlaric, licensed under CC BY-SA 3.0
Elektromagnetische Wellen sind ja eine Kombination von einem oszillierenden elektrischen Feld (E-Feld) und einem mit gleicher Frequenz oszillierenden magnetischen Feld (B-Feld). Eine Welle transportiert ja immer Energie, d.h. eine elektromagnetische Welle auch.
Analog zum Experiment mit der Leuchtstoffröhre, haben wir auch hier gleichzeitig ein E-Feld und ein B-Feld. Beide Felder stehen senkrecht zur Wellengeschwindigkeit \(\vec{v}\), deren Betrag die Lichtgeschwindigkeit \(c\) ist.
In der nachfolgenden Zeichnung wird klar, dass der Energietransport in der gleichen Richtung, wie die Wellengeschwindigkeit zeigen muss. Hier kommt Poyntings Idee eines Vektors \(\vec{S}\), der senkrecht zum \(\vec{E}\) und zu \(\vec{B}\) steht und der für den Fluss der Energie da steht.
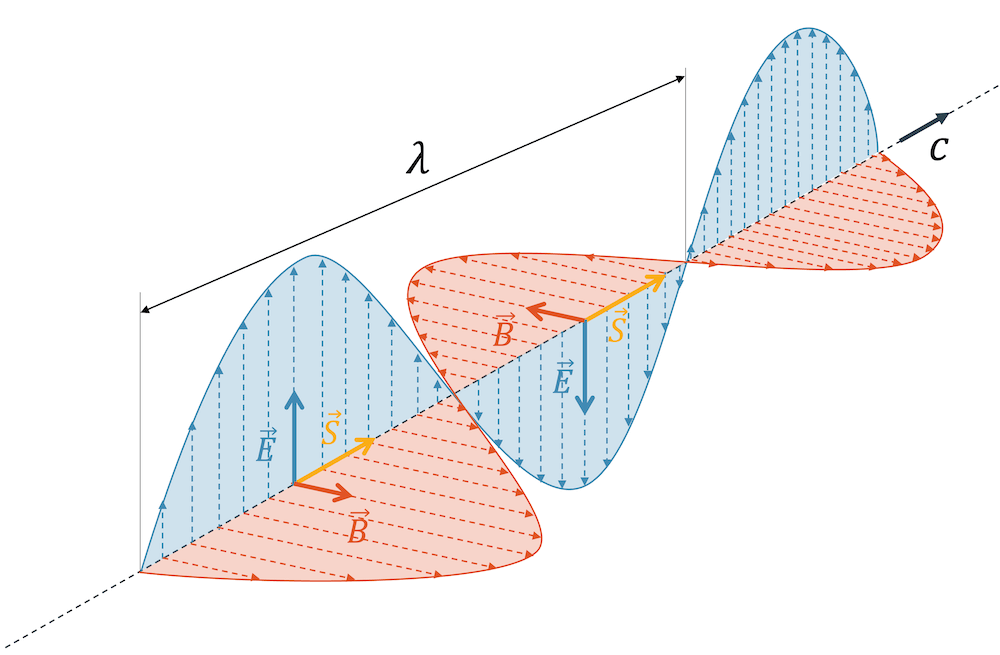
Wenn wir ganz genau hinschauen, bilden die drei Vektoren \(\vec{E}\), \(\vec{B}\) und \(\vec{S}\) ein Rechtssystem, das mathematisch durch ein Vektorprodukt ausgedrückt werden kann. Der Poynting-Vektor \(\vec{S}\) wird tatsächlich so berechnet, allerdings wird mit einem Vorfaktor der Betrag und seine Einheit angepasst:
\[ \vec{S} = \frac{1}{\mu_0} \cdot \vec{E} \times \vec{B} \]
Die Grösse \(\mu_0\) ist eine physikalische Konstante, magnetische Permeabilität des Vakuums genannt.
Poynting-Vektor als gerichtete Intensität
Der Betrag des Poynting-Vektors ist die Menge an Energie, die pro Zeit und pro Fläche fliesst. Energie pro Zeit nennen wir Leistung und benutzen dafür die Einheit \(\text{W}\) Watt. Für den Poynting-Vektor benutzen wir deshalb die Einheit Watt pro Quadratmeter:
\[ \Big[ \,\vec{S}\, \Big] = \frac{\frac{\text{J}}{\text{s}}}{\text{m}^2} = \frac{\text{W}}{\text{m}^2} \]
Eine solche Grösse wird in der Physik auch Intensität genannt.
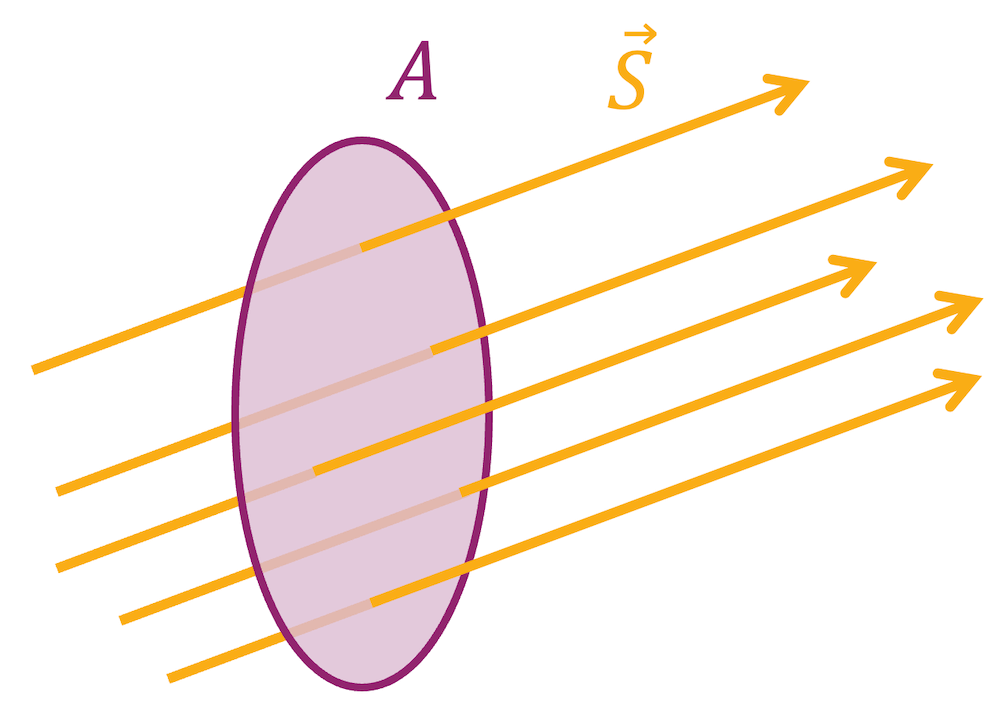
Für den Energiefluss (Leistung \(P\)) durch eine Fläche \(A\) können wir schreiben:
\[ |\vec{S}| = \frac{P}{A} \]
Energietransport beim stromdurchflossenen Leiter
Die Frage nach dem Energietransport in einem stromdurchflossenen Leiter ist gar nicht so einfach. Das hat vor allem mit dem Fluss der Ladungen im Metall zu tun, der quantenmechanisch ist und wir deshalb Mühe haben, ihn uns richtig vorzustellen.
Wir schauen uns die Felder an und stellen uns vor, dass ein Stück Leiter in der Nähe der Batterie ein höheres Potenzial hat als seine Umgebung und wir deshalb ein E-Feld haben, das vom Leiter weg zeigt. In der Elektrostatik ist es sogar so, dass die Feldlinien unbedingt senkrecht zur Leiteroberfläche zeigen müssen, da sonst die Ladungen fliessen würden.
Wir stellen uns vor, dass die Ladungen so langsam sind, dass ihre Geschwindigkeit vernachlässigt werden kann und wir deshalb die Vorstellung der Elektrostatik benutzen dürfen, obwohl ein gewisser Strom fliesst. Darauf folgend, haben wir um den Leiter herum ein E-Feld, das vom Leiter weg zeigt und im Leiter drin haben wir kein E-Feld (\(E=0\)).
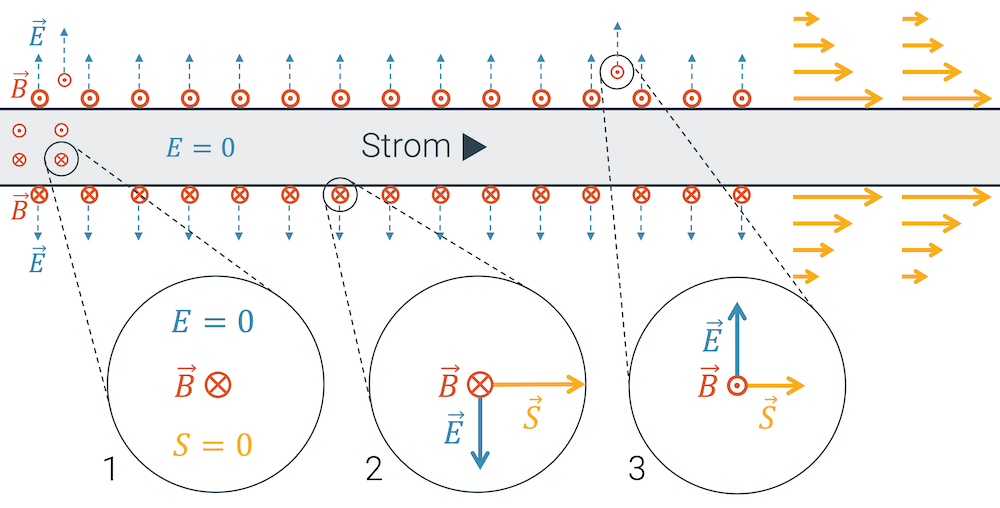
Durch die magnetische Wirkung des elektrischen Stroms wird ringförmig um den Leiter herum ein Magnetfeld (B-Feld) erzeugt. Die Stärke des Magnetfelds nimmt mit dem Abstand vom Leiter schnell ab.
Um die Richtung des B-Felds anzuzeigen, benutzen wir einen Kreis mit Punkt, wenn der Vektor aus der Zeichenebene heraus zeigt. Wenn der Vektor in die Zeichenebene hinein zeigt, benutzen wir einen Kreis mit einem Kreuz.
Im obigen Bild sehen wir in der ersten “Lupe”, dass im Leiter drin kein Poynting-Vektor sein kann, weil das E-Feld verschwindet. In der zweiten Vergrösserung kriegen wir einen Poynting-Vektor, der nach rechts zeigt. In der dritten Vergrösserung ebenfalls, jedoch ist sein Betrag kleiner, weil das B-Feld schwächer ist.
Wir haben demnach einen maximalen Energiefluss unmittelbar um den Leiter herum. Er nimmt mit Abstand vom Leiter ab. Erstaunlicherweise haben wir im Leiter keinen Energiefluss! Die Energie wird nicht von den Ladungen transportiert, sondern vom elektromagnetischen Feld um den Leiter herum.
Tatsächlich haben wir in einem realen Leiter ein ganz schwaches E-Feld, da der Leiter nicht ideal leitend ist. Der kleine elektrische Widerstand des Leiters ist für ein schwaches Gefälle des elektrischen Potenzials verantwortlich. Kombiniert mit dem Magnetfeld erhalten wir einen schwachen Poynting-Vektor , der zum Zentrum des Leiters gerichtet ist. Er stellt den Energiefluss dar, der in das Leiterinnere fliesst, um dort in Wärme umgewandelt zu werden.
Bei einem stromdurchflossenen Leiter übernimmt das elektromagnetische Feld die Aufgabe des Transports der Energie um den Leiter herum.
Wir schliessen daraus, dass im Leiter keine Energie transportiert wird, d.h. die Ladungen haben nur eine indirekte Rolle beim Energietransport. Sie stellen das B-Feld, das für den Energietransport benötigt wird.
Energiefluss bei Gleichspannung
Die Erkenntnisse über den Energietransport beim stromdurchflossenen Leiter können jetzt auf eine einfache Schaltung übertragen werden. Links haben wir die Gleichspannungsquelle. Rechts einen Verbraucher: Wir nehmen einfach eine Lampe.
Das E-Feld verläuft immer senkrecht zum Leiter und das B-Feld immer ringförmig um den Leiter herum. Daraus folgen Poynting-Vektoren um den Leiter herum: Vom Plus-Pol der Batterie hin zum Verbraucher.
Interessant ist, dass wir auch einen Energiefluss von der Batterie zum Verbraucher kriegen, wenn wir unten vom Minus-Pol der Batterie zum Verbraucher gelangen. Beide Leiter sind offenbar gleichwertig am Energietransport beteiligt. Beim unteren Leiter verläuft der Energiefluss aber entgegen dem Ladungsfluss!
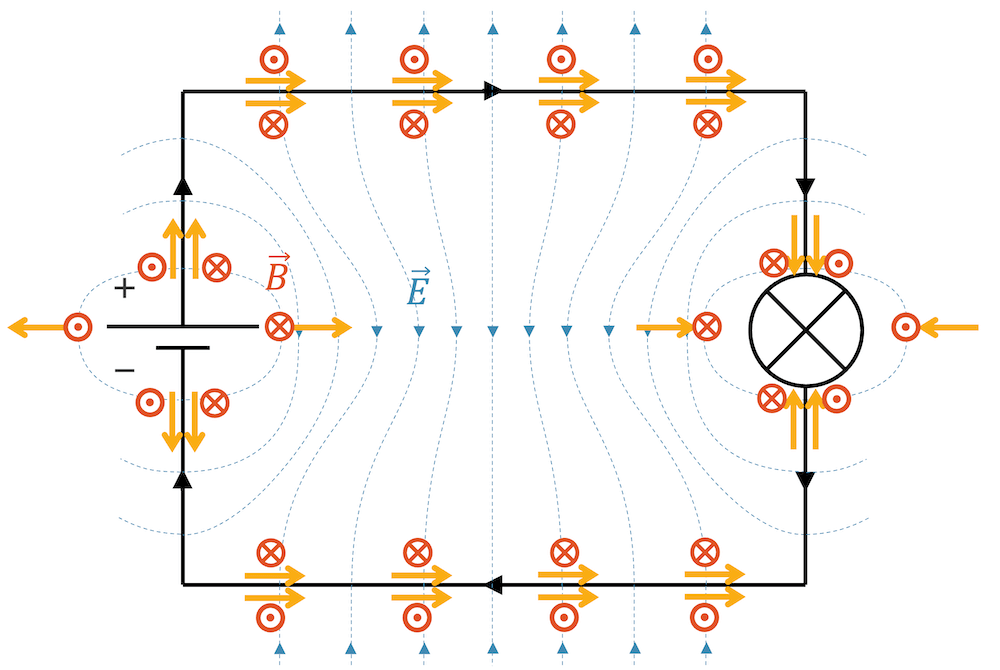
Unmittelbar um die Batterie herum gibt es Poynting-Vektoren, die einen Energiefluss von der Batterie ins Feld zeigen. Um den Verbraucher herum ist es umgekehrt. Hier zeigen Poynting-Vektoren vom Feld zum Verbraucher hin, oft quasi aus dem Nichts heraus.
Der Energiefluss in einer Schaltung verläuft um beiden Leitern herum von der Spannungsquelle zum Verbraucher. Beim Leiter, der am Minus-Pol der Spannungsquelle angeschlossen ist, ist der Energiefluss dem Ladungsfluss entgegengesetzt, womit einmal mehr gezeigt ist, dass Ladungen die Energie nicht direkt transportieren können.
Energiefluss bei Wechselspannung
Bei einer Spannungsquelle mit Wechselspannung, wie z.B. unserer Steckdose, wechselt das Vorzeichen der Spannung mit einer hohen Frequenz. Im europäischen Stromnetz beträgt die Frequenz 50 Hz, d.h. 50 mal pro Sekunde haben wir eine positive und eine negative Spannung! Die positive Spannung dauert maximal 0.01 Sekunden, bevor sie für weitere 0.01 Sekunden von einer negativen Spannung abgelöst wird.
Wenn wir bedenken, dass die Elektronen im Metall mit einer Driftgeschwindigkeit von Millimetern pro Sekunde unterwegs sind, kommen sie in der Hundertstel-Sekunde wirklich nicht weit. Die Bewegung der Elektronen muss mehr einer Art Schwingung an Ort und Stelle gleichen.
Stellt sich die Frage: Wie können Elektronen, die an Ort und Stelle sich hin und her bewegen, die Energie von der Spannungsquelle zum Verbraucher liefern?
Die Antwort liefert uns natürlich wieder der Poynting-Vektor. Im positiven Fall haben wir kurzzeitig eine Spannung von beispielsweise +5V und die Ladungen bewegen sich in der Schaltung im Uhrzeigersinn. Der Energiefluss ist wie im Fall der Gleichspannung, d.h. um den Leiter herum und an beiden Leitern von der Spannungsquelle zum Verbraucher gerichtet.
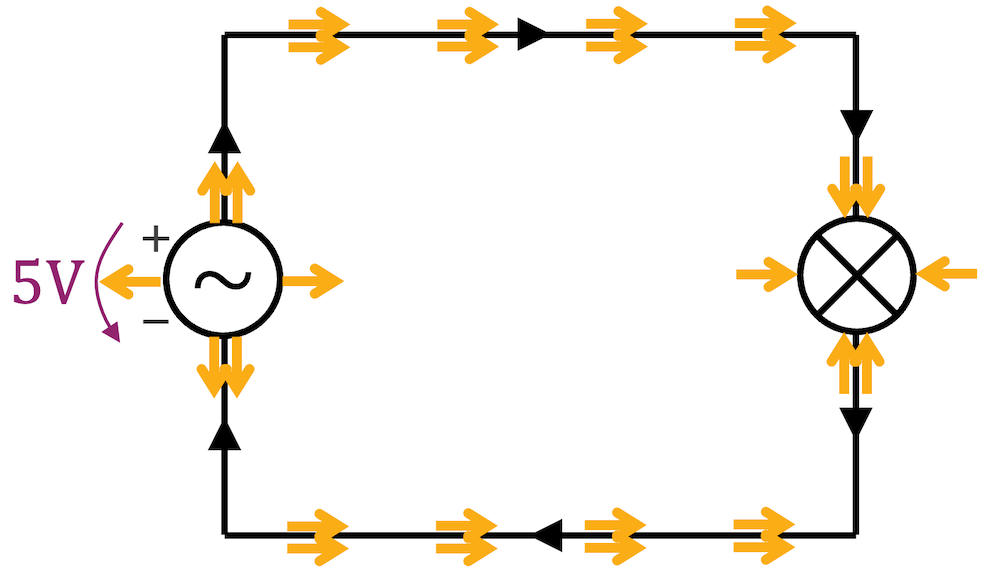
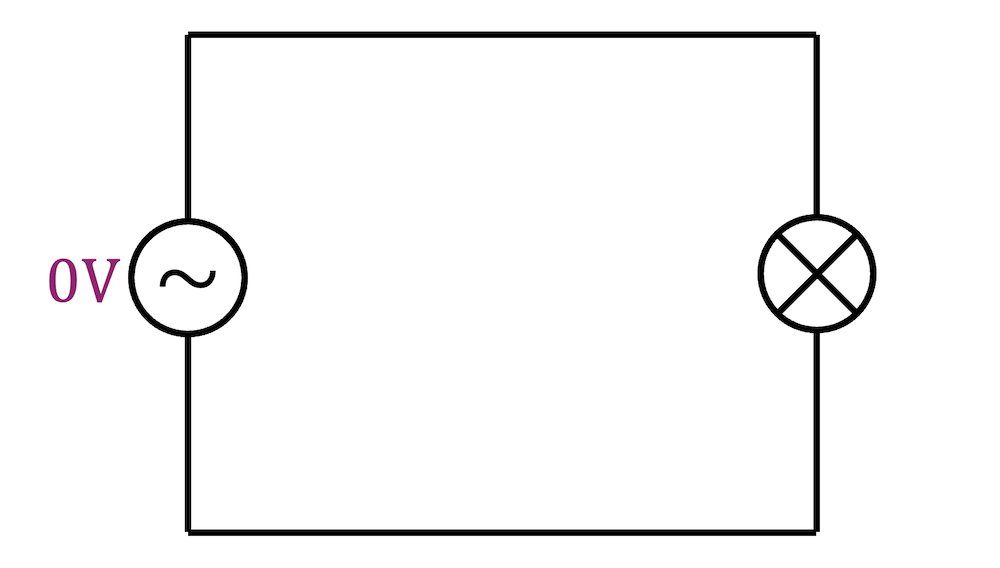
Für kurze Zeit ist die Spannung sehr klein bzw. genau null und es fliesst keine Ladung. In diesem Moment fliesst auch keine Energie. Die Ladungen transportieren die Energie zwar nicht, aber ohne Ladungsfluss haben wir kein B-Feld und damit auch keinen Energiefluss!
Danach ist hat die Spannung an der Spannungsquelle ein negatives Vorzeichen und der Ladungsfluss ist kurzzeitig im Gegenuhrzeigersinn gerichtet. Für den Energiefluss ändert sich nichts: Die Energie fliesst um beide Leiter herum von der Spannungsquelle zum Verbraucher, ganz unabhängig vom Vorzeichen der Spannung.
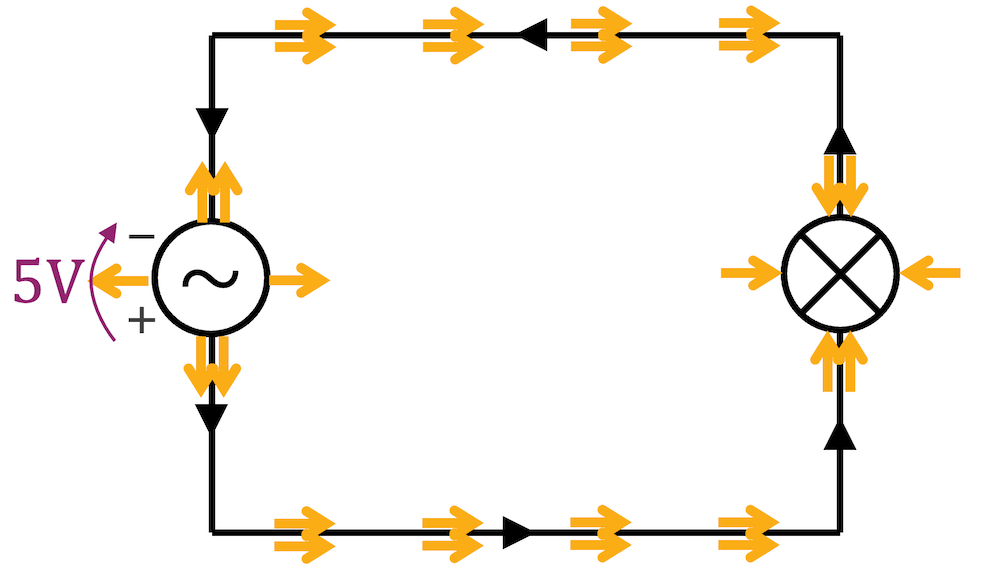
In einer Schaltung unter Wechselspannung bewegen sich die Ladungen nur hin und her, d.h. sie können unmöglich sich von der Spannungsquelle zum Verbraucher bewegen.
Trotzdem findet während der kurzen Zeit, in welcher sich die Ladungen bewegen, ein Energietransport im Feld statt, der aber immer gleich gerichtet ist, nämlich von der Spannungsquelle zum Verbraucher hin.
Koaxialkabel
Beim Koaxialkabel sind die Leiter so angeordnet, dass sie die gleiche Achse haben (was ihnen den Namen gibt). Zwischen dem Innenleiter und dem Aussenleiter ist ein isolierendes Material eingebracht, so dass sich die beiden Leiter nicht leitend berühren.
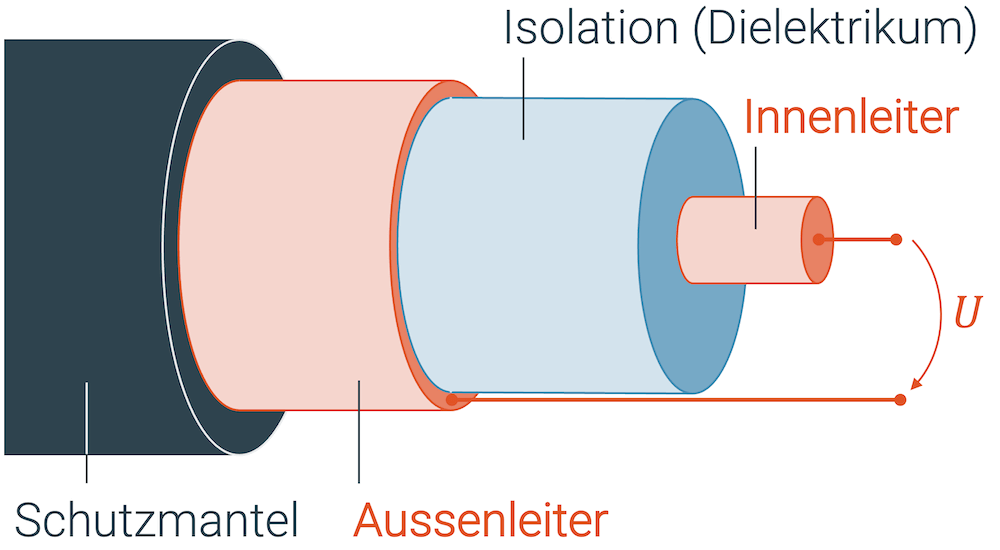
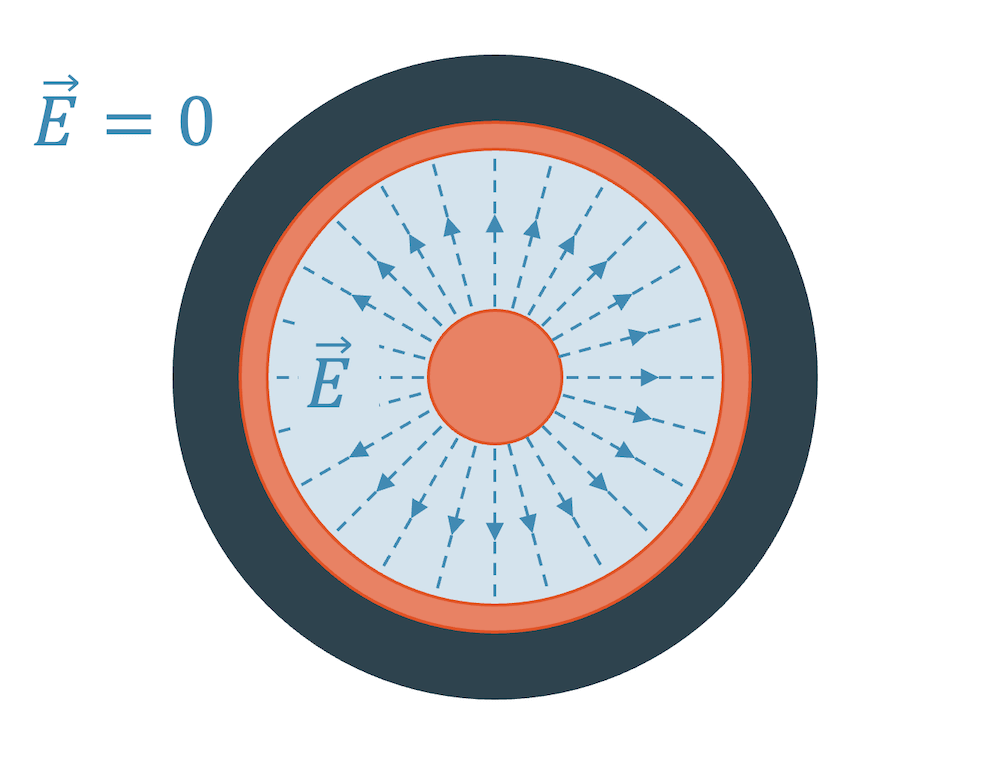
Der Vorteil dieser Anordnung ist, dass sich das E-Feld zwischen den beiden Leitern sich auf den Zwischenraum beschränkt. Ausserhalb des Koaxialkabels verschwindet das E-Feld, weil es durch den äusseren Leiter komplett abgeschirmt ist.
Wenn im Leiter drin kein E-Feld sein kann und ausserhalb des Kabels auch nicht, beschränkt sich das E-Feld wirklich auf das Dielektrikum zwischen den beiden Leitern. Nur dort kann der Poynting-Vektor nicht null sein und somit kann das Kabel nur im Dielektrikum die Energie bzw. das Signal transportieren.
Mit Koaxialkabeln erreichen wir somit, dass Felder der Aussenwelt den Energiefluss bzw. die Übertragung des Signals nicht stören können und auch dass keine Signal aus dem Kabel austreten. Koaxialkabel werden deshalb für hochfrequente, für schwache und für störungsempfindliche Signalübertragungen eingesetzt.
Beim Koaxialkabel beschränkt sich das E-Feld auf das Dielektrikum, ein nicht-leitendes Material, das zwischen den beiden Leitern eingefasst ist.
Der Energietransport bzw. die Übertragung des Signals findet nur im Dielektrikum statt, weil nur dort der Poynting-Vektor nicht verschwindet.
Koaxialkabel erlauben die Übertragung eines Signals ohne elektromagnetische Störung von aussen. Auch fliesst das Signal hier im Kabel drin und nicht wie bei anderen Kabeln, um das Kabel herum.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.