
Kondensatoren sind sehr wichtige elektronische Bauteile zur Speicherung von elektrischer Energie. Sie können nicht besonders viel Energie speichern, dafür aber schnell und unkompliziert Energie aufnehmen oder abgeben. Die Energie wird in Form eines elektrischen Felds gespeichert, das sich zwischen zwei geladenen Platten aufbaut. Die Platten berühren sich nicht, so dass keine Ladungen von der einen auf die andere Platte fliessen können. Das elektrische Feld ist im Plattenkondensator homogen, d.h. im Zwischenraum überall gleich stark. Ausserhalb des Kondensators haben wir kein elektrisches Feld, da der Effekt der beiden Platten sich gegenseitig aufhebt.
Beim Aufladen eines Kondensators steigt die Menge an Ladung \(Q\) und die Spannung \(U\) über dem Kondensator an. Kondensatoren mit einer grossen Kapazität \(C\) können viel Ladung speichern, bis ihre maximale Spannung erreicht ist. Bestimmte Materialien mit grosser relativer Dielektrizitätskonstante polarisieren zwischen den Platten und vergrössern so die Kapazität des Kondensators um Faktoren.
Plattenkondensator
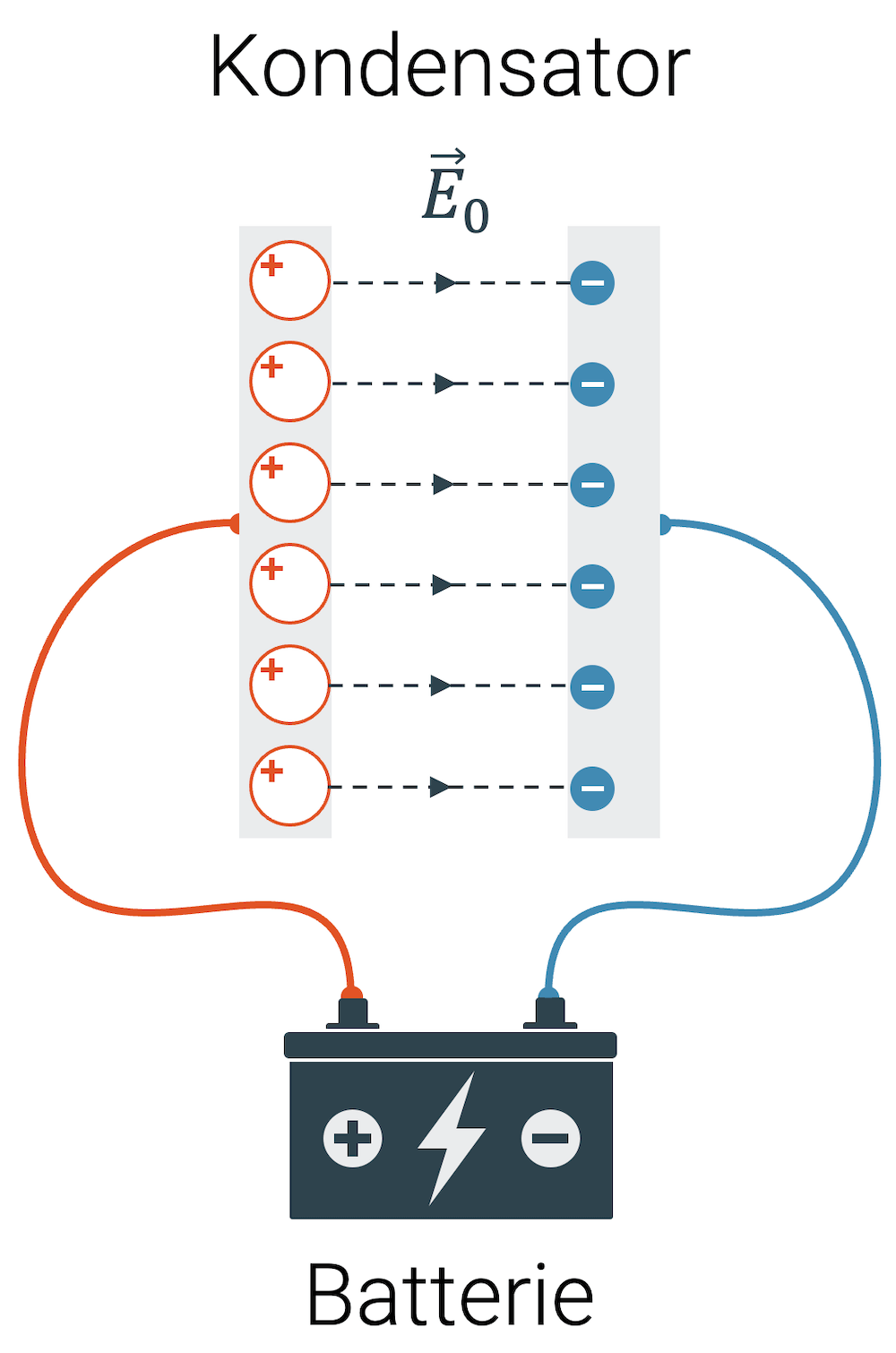
Die allermeisten Kondensatoren sind Plattenkondensatoren. Sie bestehen aus zwei Platten, die durch einen kleinen Abstand getrennt sind. Die Platten dürfen sich auf keinen Fall berühren. Zwischen ihnen ist im Normalfall eine isolierende Schicht eingebracht, die ein Berühren verhindert.
Kondensatoren werden in Schaltplänen mit zwei Querstrichen dargestellt, die den Stromkreis unterbrechen, d.h. von einer Lücke getrennt sind. Dies veranschaulicht natürlich sehr schön, dass hier tatsächlich zwei Platten eingebaut sind, die von einer nicht-leitenden Lücke getrennt sind.
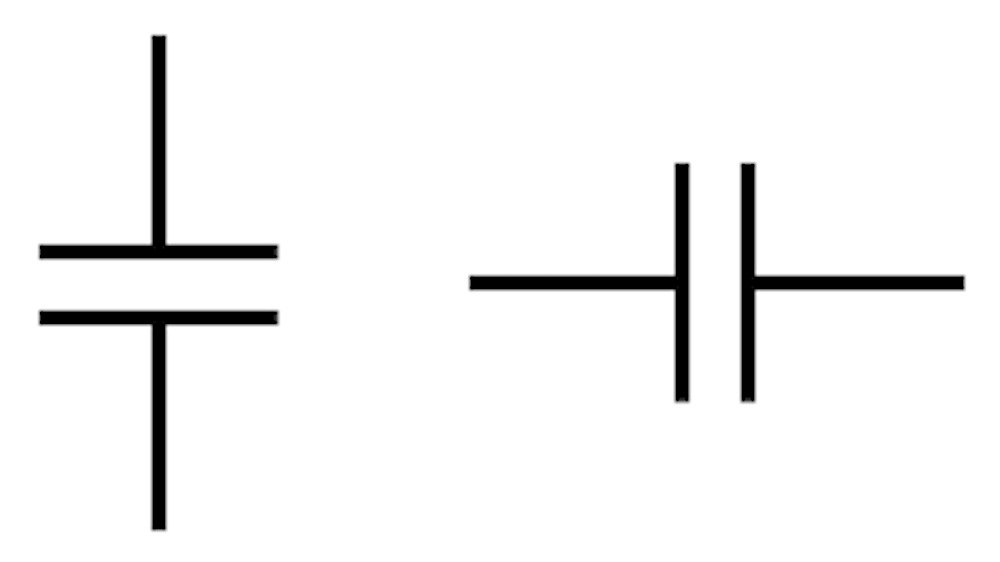
Um die Fläche der Platten möglichst gross, den Kondensator aber immer noch möglichst kompakt zu halten, sind die Flächen meistens aus einer dünnen Metallfolie, aussen mit einer isolierenden Schicht geschützt und dann gerollt.
Jetzt können wir den Kondensator laden, z.B. mit einer Batterie. Die Platten werden je an die beiden Pole der Batterie angeschlossen, so dass sie sich positiv und negativ laden. Der elektrische Strom fliesst dabei in einer Richtung: Von der Batterie zur positiven Platte und von der negativen Platte zurück zur Batterie. Die Ladungen auf den Platten ziehen sich gegenseitig mit der Coulombkraft an.
Aufladen eines Kondensators
Wir werden den Prozess des Aufladens hier etwas genauer anschauen. Zuerst haben wir einen entladenen Kondensator. Seine beiden Platten sind ungeladen oder ladungsneutral, deshalb hat er weder Energie geladen, noch besteht eine elektrische Spannung zwischen den Platten: \(U=0\,\text{V}\).
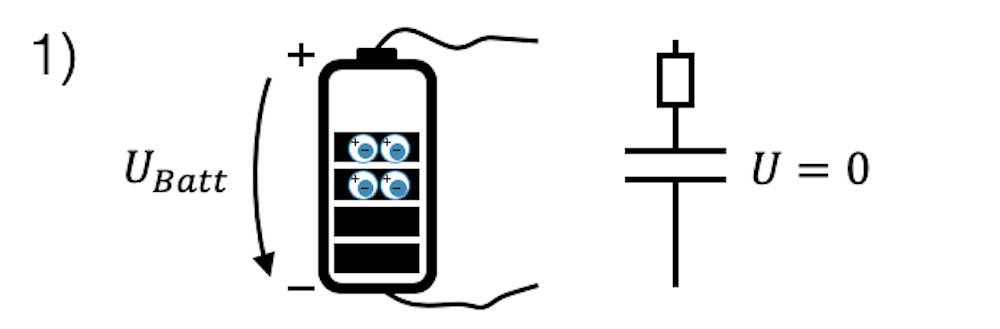
Wir schliessen jetzt die Batterie an den Kondensator an. Der ”Ladungsdruck” am Pluspol macht, dass Strom zur ersten Platte fliesst und sie anfängt positiv zu laden. Wir können uns positive Löcher vorstellen, die von der Batterie zum Kondensator fliessen oder, dass negative Elektronen in Wirklichkeit von der Platte zur Batterie fliessen. Es ist üblich den Strom von positiven Ladungen einzuzeichnen und deshalb zeigt der Strompfeil von der Batterie zur ersten Platte des Kondensators.
Bei der zweiten Platte ist der Vorgang gleich, aber gerade umgekehrt im Vorzeichen. Der negative Pol der Batterie ”saugt” gewissermassen positive Ladungen von der zweiten Platte ab, so dass sie negativ geladen wird. Auch hier können wir uns den umgekehrten Fluss von negativen Elektronen vorstellen, die am negativen Pluspol der Batterie gewissermassen im Überfluss vorhanden sind und jetzt von den positiven Ladungen der ersten Platte angezogen werden. Sie wandern zur zweiten Platte um möglichst nahe zu den positiven Ladungen zu kommen.
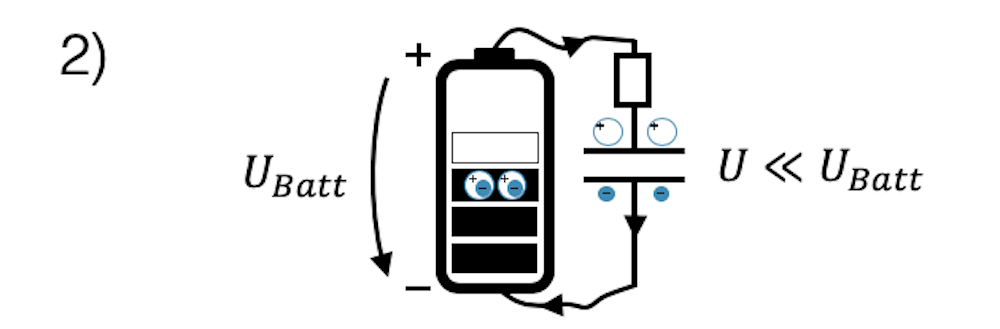
Mit dem oben beschriebenen elektrischen Strom wird der Kondensator immer mehr aufgeladen. Irgendwann sind die Platten aber so stark mit Ladungen besetzt, dass die Abstossungskräfte der gleichartigen Ladungen auf der Platte gleich stark werden, wie die Anziehung der anderen Ladungen. Die ”Motivation” für weitere Ladungen zur Platte zu fliessen fällt weg und der Strom klingt ganz ab. Der Kondensator ist jetzt voll aufgeladen und hat die gleiche Spannung \(U\), wie die Batterie, die ihn aufgeladen hat.
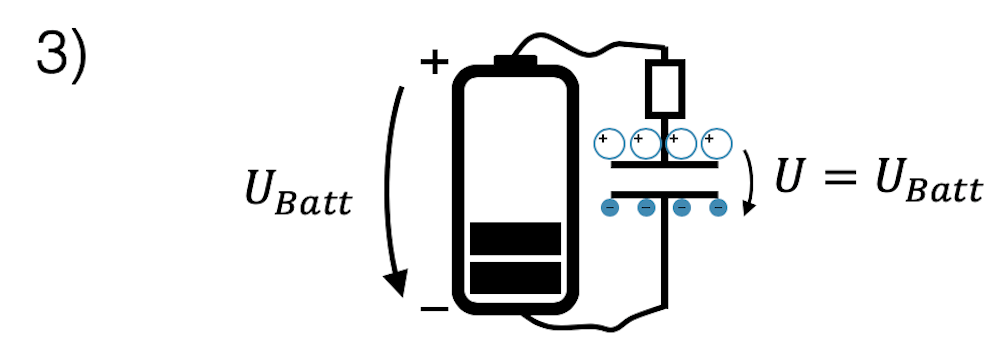
Trennen wir die leitende Verbindung von Batterie zu Kondensator, so passiert nichts, denn in den Leitungen fliesst kein Strom mehr. Der Kondensator behält aber seine Ladung, denn die Ladungen bleiben von den andersartigen Ladungen auf der anderen Platte angezogen. Wir haben jetzt einen voll aufgeladenen Kondensator mit einer Spannung \(U\) zwischen den Platten. Er hat einen Teil der Energie der Batterie aufgenommen und ist in der Lage, diese Energie wieder abzugeben.
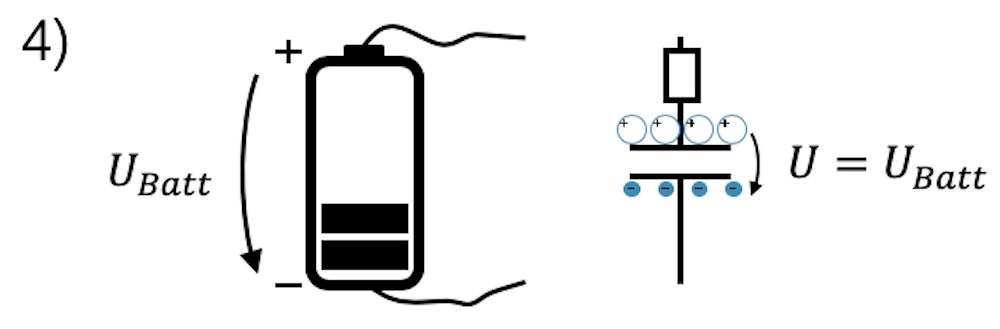
Elektrisches Feld im Kondensator
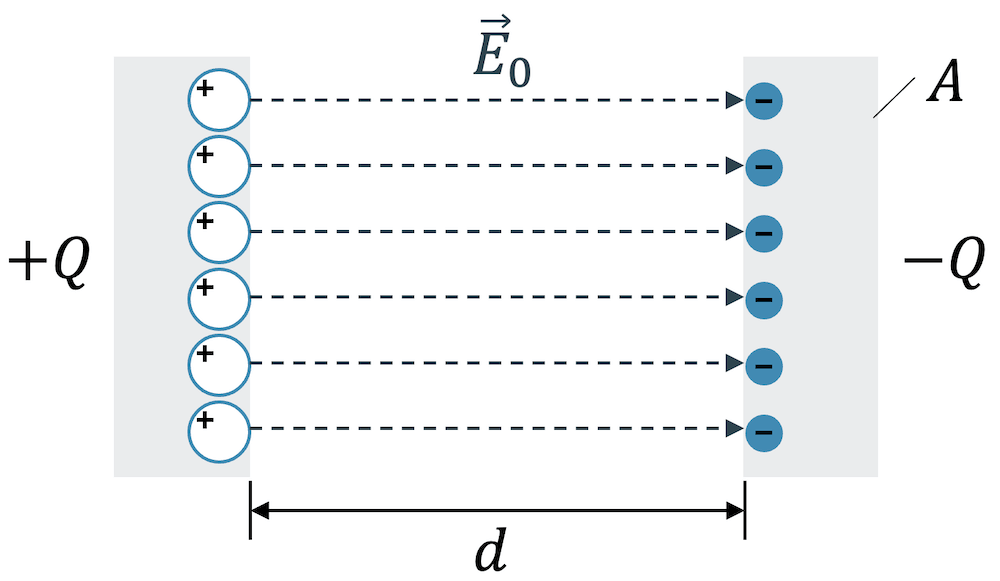
Wenn wir die zwei Platten vergrössern, haben wir zwei Platten mit entgegengesetzten Ladungen, die sich gegenüberstehen. Zwischen den Ladungen entsteht ein elektrisches Feld. Weil die Feldlinien parallel sind, sind sie zwischen den Platten immer gleich dicht und somit ist das elektrische Feld gleich stark. Die Stärke dieses E-Felds ist abhängig von der Ladungsmenge auf den beiden Platten \(Q\) und der Fläche der Platten \(A\):
\[ E_0 = \frac{Q}{\varepsilon_0 A} \]
Je kleiner die Platten, desto konzentriert sind die Ladungen angeordnet, was eine erhöhte Dichte der Feldlinien und somit eine grössere Stärke des E-Felds bedeutet.
Die Grösse \(\varepsilon_0\) ist die Permittivität des Vakuums, auch elektrische Feldkonstante oder Dielektrizitätskonstante des Vakuums genannt. Sie ist eine physikalische Konstante, die meistens im Taschenrechner schon gespeichert ist:
\[ \varepsilon_0 = 8.854 \cdot 10^{-12}\,\frac{\text{C}^2}{\text{J m}} \]
Interessant ist noch die Tatsache, dass das elektrische Feld ausserhalb des Kondensators null ist. Eigentlich müssten die Ladungen auf der Platte ein elektrisches Feld in alle Richtungen erzeugen. Eigentlich tun sie das auch, aber die Ladungen auf der anderen Platte erzeugen ein entgegengesetztes Feld, das dieses wieder aufhebt. Beide Felder addieren sich in ihrer Wirkung zwischen den Platten, neutralisieren sich aber wieder ausserhalb des Kondensators. Das ist natürlich ein grosser Vorteil, denn in einem elektronischen Gerät wäre es ungünstig, wenn die Elektronen in den Leitern von den vielen Kondensatoren eine Coulombkraft spüren würden.
Beachte, dass der Abstand \(d\) zwischen den beiden Platten keinen Einfluss auf die Stärke des E-Felds, wohl aber auf die Kapazität \(C\) des Kondensators hat.
Kapazität
Kondensatoren sind Energiespeicher – deshalb ist von besonderem Interesse, wie viel sie speichern können. Ihr Speichervermögen wird aber nicht mit der Energie- oder Ladungsmenge quantifiziert, sondern mit der einer eigenen Grösse, der sog. Kapazität \(C\).
Was unter der Kapazität zu verstehen ist, lässt sich am besten beim Aufladen eines Kondensators veranschaulichen: Zuerst sind die Platten entladen (\(Q = 0\,\text{C}\)). Die Spannung über den beiden Platten ist auch null: \(U = 0\,\text{V}\). Wenn wir jetzt den Kondensator laden, nimmt die Ladung \(Q\) und die Spannung \(U\) zu. Wir können uns das ein bisschen wie das Füllen einer Badewanne vorstellen. Je mehr Wasser (=Ladung) in die Wanne geflossen ist, desto höher ist der Füllstand (=Spannung):
\[ Q = C \cdot U \]
Wenn wir jetzt eine bestimmte Ladungsmenge \(Q\) nehmen und sie in einen Kondensator laden, der eine kleine Kapazität \(C\) hat (kleine Wanne), dann ist \(U\) dafür gross. Der kleine Kondensator ist somit auch früher voll. Bei einem Kondensator mit sehr grosser Kapazität (Swimmingpool), steigt für die gleiche Ladungsmenge die Spannung nur wenig an und wir können noch lange füllen, bevor wir die Batteriespannung \(U_{Batt}\) erreichen.
Wenn wir jetzt die Beziehung nach \(U\) auflösen, erhalten wir eine lineare Beziehung für \(U(Q)\):
\[ U = \frac{1}{C} \cdot Q \]
Wir können deshalb in einem \(U,Q\)-Diagramm einen linearen Verlauf zeichnen mit der Steigung \(\frac{1}{C}\).
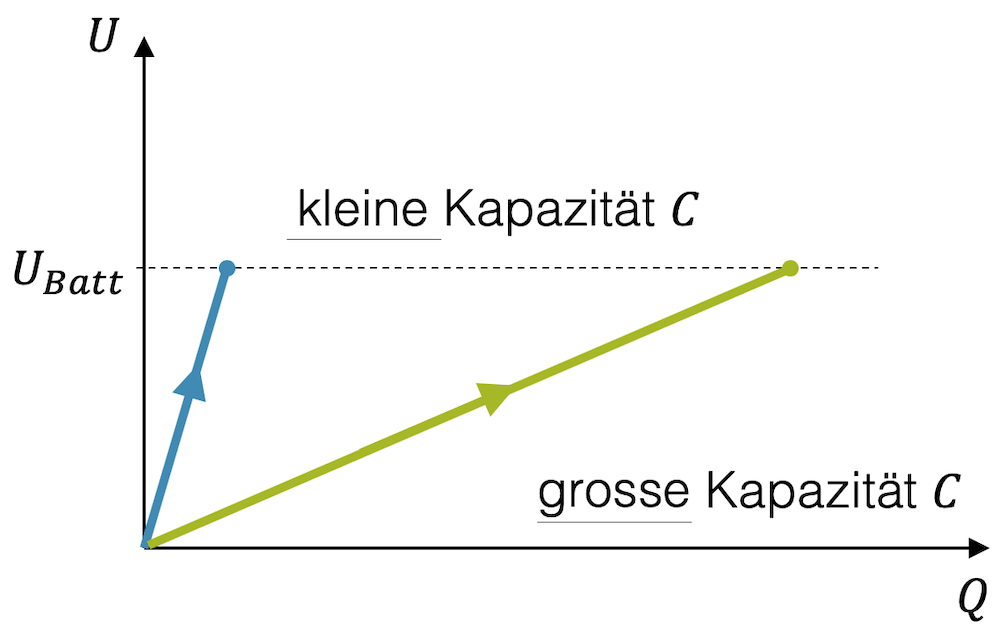
Im Diagramm sehen wir sehr schön, dass ein Kondensator mit kleiner Kapazität \(C\) eine grosse Steigung des linearen Verlaufs \(U(Q)\) aufweist. Die Batteriespannung ist relativ schnell erreicht und der Kondensator ist voll, hat aber nicht besonders viel Ladung aufnehmen können. Umgekehrt ist bei einem Kondensator mit grosser Kapazität \(C\) die Batteriespannung erst mit einer grossen Ladungsmenge \(Q\) erreicht.
Die Kapazität \(C\) eines Kondensators bestimmt, wie schnell die Spannung \(U\) mit zunehmender Ladung \(Q\) zunimmt:
\[ Q = C \cdot U \qquad \rightarrow \qquad U = \frac{1}{C} \cdot Q \]
Abkürzung: \(C\)
Einheit: \([\,C\,] = \text{F} = \frac{\text{C}}{\text{V}} \quad\) (Farad)
Die Einheit Farad ist nach dem grossen britischen Experimentalphysiker Michael Faraday (1791 – 1867) benannt.
Für einen Plattenkondensator lässt sich die Kapazität \(C\) anhand der Fläche der Platten \(A\) und deren Abstand \(d\) berechnen:
\[ C = \varepsilon_0 \cdot \frac{A}{d} \]
Dabei ist \(\varepsilon_0\) die elektrische Feldkonstante bzw. Permittivität des Vakuums:
\[ \varepsilon_0 = 8.854 \cdot 10^{-12} \; \frac{\text{As}}{\text{Vm}} \]
Durch das Einbringen eines Dielektrikums zwischen die beiden Platten, lässt sich die Kapazität eines Kondensators um Faktoren vergrössern. Grund dafür ist die Polarisation des Dielektrikums und die damit verbundene Verkleinerung des elektrischen Felds bei gleicher Ladung.
Energie im Kondensator
Um besser zu verstehen, wie Energie in den Kondensator kommt, vergleichen wir den entladenen Kondensator vorher mit dem geladenen Kondensator nachher. Der entladene Kondensator ist ladungsneutral: alle positiven Löcher sind mit negativen Ladungen besetzt. Wenn wir einen Kondensator aufladen, nimmt die Anzahl positiver Ladungen auf der einen Platte gleich zu, wie die Anzahl negativer Ladungen auf der anderen Platte. Im Prinzip könnte man sich vorstellen, wie die negativen Ladungen von der einen Platte auf die andere Platte gehen und dort positive Löcher zurücklassen.
Natürlich geht die negative Ladung nicht wirklich von der einen Platte auf die andere, denn da gibt es keine leitende Verbindung, die einen Ladungsfluss ermöglichen würde. Die negative Ladung geht auf die andere Seite, Richtung Batterie, meistens aber nur einen kurzen Weg. Dort geht dann eine andere negative Ladung einen kurzen Weg weiter Richtung Batterie und gibt die ”Bewegung” an eine nächste negative Ladung weiter etc. Es ist wie in einem Stafettenlauf. In Summe ist aber eine negative Ladung von der oberen Platte weggegangen und eine negative Ladung auf der unteren Platte angekommen.
Wie viel Energie braucht es jetzt, um eine Ladung von der einen Platte auf die andere zu bringen? Auch wenn die Ladungen in Wirklichkeit den Umweg über die Batterie nehmen, ist das Resultat das Gleiche. Bei Energiebetrachtungen reicht es aus, das vorher mit dem nachher zu vergleichen.
Um eine kleine Ladungsmenge \(\Delta Q\) vom tieferen Potenzial \(\varphi_B\) auf das höhere Energiepotenzial \(\varphi_A\) anzuheben, muss an der Ladung die kleine Arbeit \(\Delta W\) geleistet werden:
\[ \Delta W = \Delta Q \cdot (\varphi_A – \varphi_B) = \Delta Q \cdot U \]
Dabei haben wir für die Potenzialdifferenz die elektrische Spannung \(U = (\varphi_A – \varphi_B)\) eingesetzt, die zwischen den beiden Platten herrscht. In einem \(U,Q\)-Diagramm können wir das Produkt \(\Delta Q \cdot U\) als Rechteckfläche darstellen. Die Arbeit \(\Delta W\) entspricht der Fläche des Rechtecks mit Grundseite \(\Delta Q\) und Höhe \(U\). Es ist die Menge an Energie, die von der Batterie in den Kondensator geflossen ist, indem die Batterie den Kondensator um eine kleine Ladungsmenge \(\Delta Q\) aufgeladen hat.
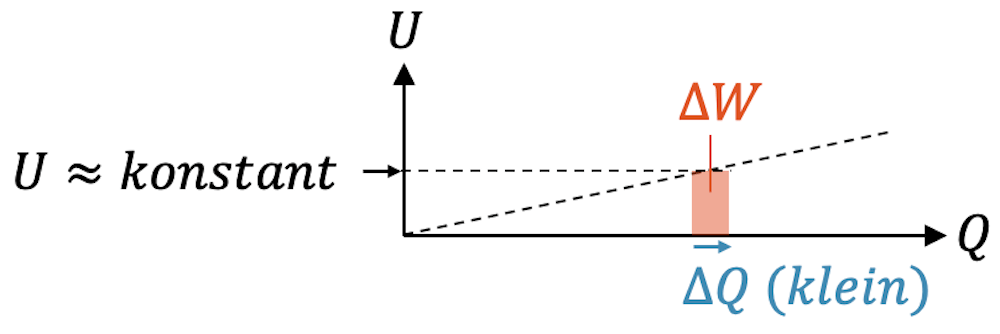
Wir wissen, dass die Spannung beim Aufladen des Kondensators linear mit der Ladungsmenge ansteigt. Für die Bestimmung der Energie müssen wir deshalb unendlich viele schmale Rechtecke aneinanderreihen und deren Höhe immer ein bisschen anwachsen lassen. Die Summe aller schmalen Rechtecke mit der Fläche \(\Delta W_i\) ergibt dann die ganze Energie, die in den Kondensator gesteckt worden ist. Sie entspricht der Fläche unterhalb des Spannungsverlaufs, was einem Dreieck entspricht.
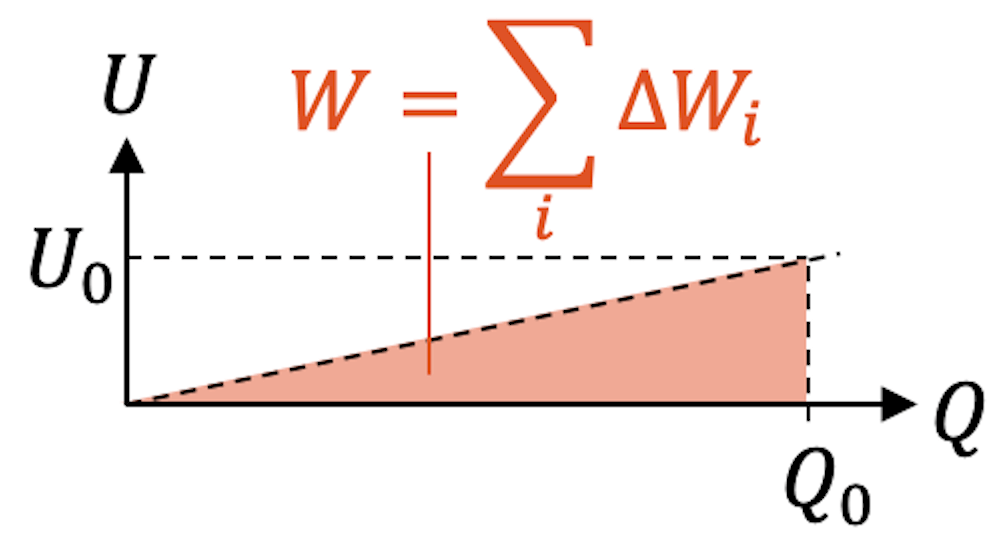
Die Fläche des Dreiecks lässt sich sich einfach schreiben als die Hälfte des Rechtecks mit den Seitenlängen \(Q_0\) und \(U_0\). \(Q_0\) ist die Gesamtladung des Kondensators und \(U_0\) die Spannung, auf welche er aufgeladen worden ist.
\[ W = \frac{1}{2} Q_0 U_0 \]
Wenn wir jetzt für die Ladung \(Q = C \cdot U\) bzw. \(Q_0 = C \cdot U_0\) einsetzen, erhalten wir für die Energie des Kondensators:
\[ W = \frac{1}{2} C U_0^2 \]
In gleicher Art können wir einen Ausdruck für die Energiedichte im Kondensator finden, d.h. für die Energie pro Volumen. Wir starten wieder mit der Dreiecksfläche und ersetzen die Ladung mit der Formel für das elektrische Feld im Plattenkondensator:
\[ E_0 = \frac{Q}{\varepsilon_0 A} \qquad \rightarrow \qquad Q = \varepsilon_0 E_0 A \]
Für die Spannung \(U\) setzen wir ein
\[ U = E_0 d \]
Das gibt uns für die Energie \(W = \frac{1}{2} Q_0 U_0\):
\[ W = \frac{1}{2} \cdot \varepsilon_0 E_0 A \cdot E_0 d = \frac{1}{2} \varepsilon_0 E_0^2 \cdot A d \]
Am Schluss steht \(Ad\). Die Fläche der Platten mal deren Abstand gibt uns genau das Volumen des Zwischenraums. Wenn wir den Ausdruck für die Energie durch das Volumen teilen, erhalten wir die Energie pro Volumen, oder eben die Energiedichte, die wir mit einem kleinen Buchstaben \(w\) schreiben:
\[ w = \frac{1}{2} \varepsilon_0 E_0^2 \]
Die Energie zwischen den Platten liegt also im elektrischen Feld.
Für einen geladenen Kondensator der Kapazität \(C\) können wir die Energie bestimmen anhand der Ladung \(Q\) bzw. Spannung \(U\):
\[ W = \frac{1}{2} Q U = \frac{1}{2} C U^2 \]
Die Energie im Kondensator liegt im elektrischen Feld. Für die Energiedichte \(w\) (Energie pro Volumen) in einem Plattenkondensator gilt:
\[ w = \frac{1}{2} \varepsilon_0 E_0^2 \]
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.