Elektrische Spannung

Die elektrische Spannung ist die Differenz von zwei elektrischen Potenzialen \(\varphi_A\) und \(\varphi_B\). Sie hat deshalb die gleiche Einheit wie das elektrische Potenzial, das für Energie pro Ladung steht:

\[ U = \varphi_A – \varphi_B = \frac{E_A – E_B}{q} = \frac{\Delta E}{q} \qquad \rightarrow \qquad \Delta E = q \cdot U \]

Um die Ladung \(q\) vom elektrischen Potenzial \(\varphi_A\) auf das Potenzial \(\varphi_B\) ”anzuheben” braucht es Energie. Die Ladung wird gewissermassen ”aufgeladen”. Danach hat diese Ladung die Energie zur Verfügung und kann sie elektrisch wieder abgeben.

Die Spannung \(U\) ist deshalb die Energie pro Coulomb Ladung, die gegenüber dem Potenzial \(\varphi = 0\,\text{V}\) zur Verfügung steht.

Definitionen

Abkürzung: \(U\)

Einheit: \([\,U\,] = \text{V} = \frac{\text{J}}{\text{C}}\quad\) (Volt)

Spannungsquellen

Spannungsquellen stellen die elektrische Spannung zur Verfügung, die für den Betrieb von elektrischen Geräten oder Systemen gebraucht werden. Die elektrische Spannung stellt, gegenüber dem Potenzial der Erde, die potenzielle Energie dar, die Ladungen auf dem höheren Potenzial zur Verfügung haben. Konkret sind das letztlich die bereitstehenden Elektronen und ihre Energie.

Es wird unterschieden zwischen zwei Arten von Spannung:

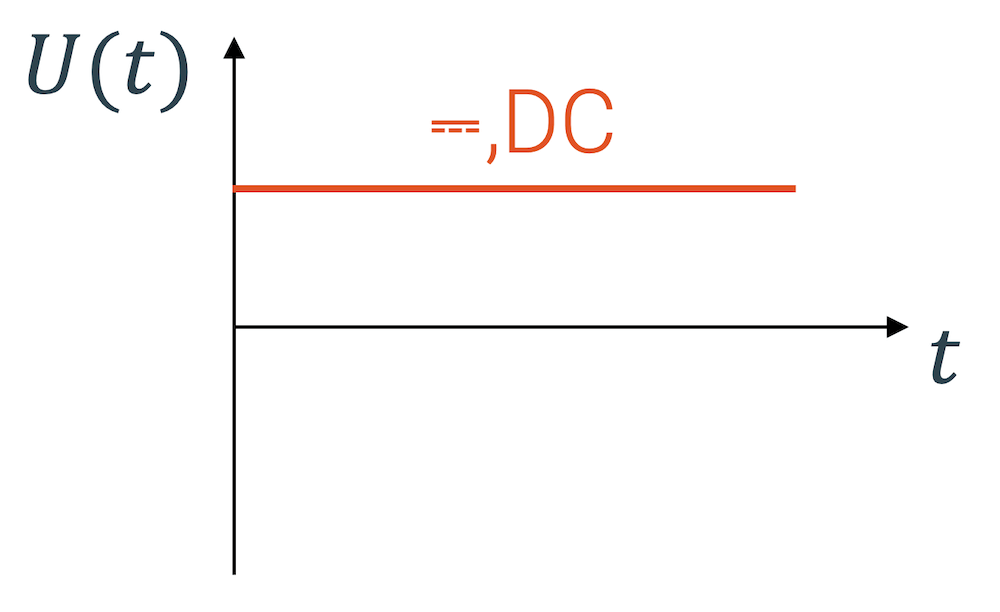
• Gleichspannung: \(\Large{⎓}\) (”Direct Current” electricity = DC)
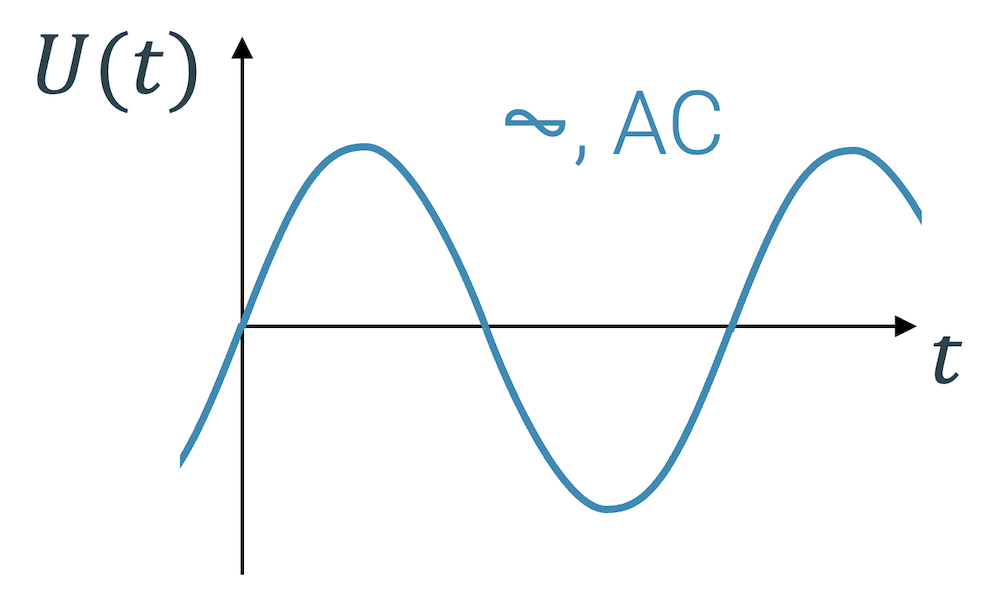
• Wechselspannung: \(\Large{⏦}\) (”Alternating Current” electricity = AC)

Die Gleichspannung bleibt mit der Zeit – wie der Name schon sagt – immer schön konstant. Es ist die Art von Spannung, die wir typischerweise von Batterien erhalten. Die Wechselspannung schwingt sehr schnell hoch und runter. Der Verlauf der Spannung über die Zeit ist eine Sinuskurve. Für einen unendlich kurzen Augenblick ist die Spannung sogar null. Unser Stromnetz liefert Wechselspannung. Der Wechsel der Spannung ist sehr schnell (50 mal hoch und wieder runter pro Sekunde!). Viele Lichter flackern eigentlich fünfzig Mal pro Sekunde. Wir merken das aber nicht. Mit einer Slow-Motion-Aufnahme kann dieses Flackern manchmal sichtbar gemacht werden.

Bei hoher Spannung hat jedes Elektron viel Energie anzubieten. Hohe Spannungen werden gebraucht für starke Motoren der Eisenbahn oder Industrie. Hier sprechen wir von ein- bis zweistelligen Kilovolts.

Für Geräte zu Hause haben wir eine Spannung von 230 V zur Verfügung. Das ist immer noch sehr viel Energie pro Ladung und kann, falls sie fehlgeleitet wird, zu einem Hausbrand oder zu einem tödlichen Elektroschock führen. Diese Art von Energie wird aber für energiehungrige Geräte wie das Bügeleisen, der Backofen, Wasserkocher, Haarföhn oder Staubsauger gebraucht.

Für kleinere Geräte oder Spielzeuge nimmt man Batterien oder Akkus zur Hand. Sie haben eine Spannung von 1.5 V bis 5 V. Das ist so wenig Energie pro Ladung, dass wir sie mit unseren Sinnen kaum mehr wahrnehmen können. Wir können Batterien ungeschützt anfassen.

Spannungsquellen:

Batterien / Akkus (=wiederaufladbare Batterien): 1.5 V – 24 V (⎓)

• USB-Anschluss: 5 V (⎓)
• Brennstoffzellen, Solarzellen: 0.5 – 0.6 V (⎓)
• Stromnetz zu Hause: 230 V (⏦)
• Lokales Stromnetz (Quartier/Dorf): 4 – 70 kV (⏦)
• Fahrleitung einer Bahn: 15 kV (⏦)
• Übertragungsleitungen: 230 – 500 kV (⏦)

Das elektrische Potenzial

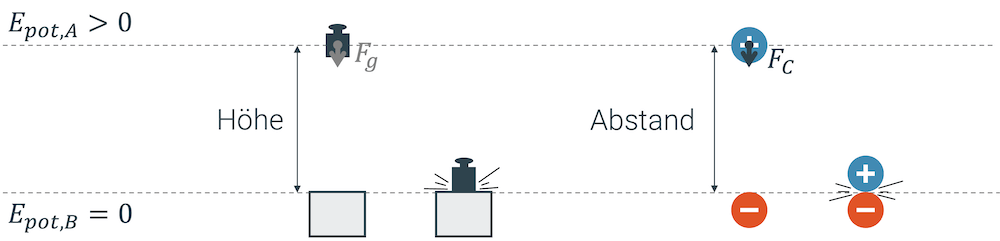
Ein Gewicht, das entgegen der Gravitationskraft angehoben ist, hat potenzielle Energie. Wir mussten das Gewicht mühsam hochkurbeln, d.h. wir haben dafür Arbeit geleistet. Unsere Energie ist in das Gewicht geflossen. Heben wir 1 kg bis auf eine bestimmte Höhe \(h\) an, dann hat dieses Gewicht eine bestimmte Menge an Energie. Heben wir aber stattdessen 2 kg an, so haben wir natürlich die zweifache Energie. Es war ja auch doppelt so streng, um die 2 kg hochzukurbeln.

Bei elektrischen Ladungen ist das nicht ganz anders. Wir können Ladungen haben, die gewissermassen ”angehoben” sind und Energie beinhalten und solche, die keine Energie haben. Wenn wir eine Ladung von einer anderen Ladung mit umgekehrtem Vorzeichen wegziehen, so müssen wir gegen die Coulombkraft arbeiten.

Bringen wir eine Ladung von +1C auf einen gewissen Abstand \(r\), so haben wir z.B. 40 J Energie gespeichert. Bringen wir stattdessen die fünffache Ladung +5C auf den gleichen Abstand, so haben wir natürlich die fünffache Arbeit geleistet und jetzt auch die fünffache Energie (200 J) gespeichert.

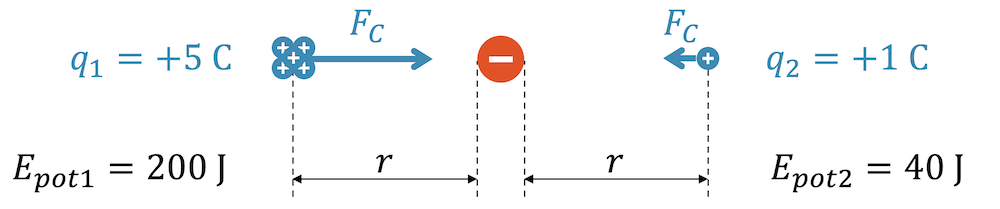
Die potenzielle Energie der Ladung ist von der Ladungsmenge abhängig. Wenn wir aber wissen möchten, wie viel Energie jedes Elektron hat, teilen wir die Energie durch die Anzahl Elektronen. Statt mit einzelnen Elektronen, arbeiten wir mit der Ladungsmenge von 1 Coulomb. Im linken Fall haben wir 200 J auf 5 C verteilt; rechts sind 40 J auf 1 C verteilt. Die Energie pro Ladung heisst auch elektrisches Potenzial und wird mit dem griechischen Buchstaben \(\varphi\) (”Phi”) abgekürzt. Für den Bruch \(\frac{\text{J}}{\text{C}}\) haben wir die neue Einheit \(\text{V}\) (Volt) eingeführt.

\[ \varphi_1 = \frac{200\,\text{J}}{5\,\text{C}} = 40\,\text{V} \quad \quad \quad \varphi_2 = \frac{40\,\text{J}}{1\,\text{C}} = 40\,\text{V} \]

Die elektrische Ladung ist in beiden Fällen gleich stark ”aufgeladen” oder jedes Elektron hat links wie rechts gleich viel Energie abzugeben. Links hat es einfach fünf mal mehr davon, aber die Elektronen sind links gleich ”mächtig” wie rechts.

Da die Ladung in der Mitte quasi dem ”Nullzustand” von Energie entspricht, haben wir zwischen den beiden Ladungen und der Zentralladung eine Differenz in elektrischem Potenzial von \(40 V – 0 V\) und somit eine elektrische Spannung von \(40 V\).

Je weiter wir die Ladung von der Zentralladung wegziehen, desto mehr Energie hat sie gespeichert. Wenn wir das elektrische Potenzial \(\varphi(r)\) als Funktion des Abstands auftragen, erhalten wir für die negative Zentralladung einen charakteristischen Verlauf einer Art ”Schlucht” oder ”Topf” (links).

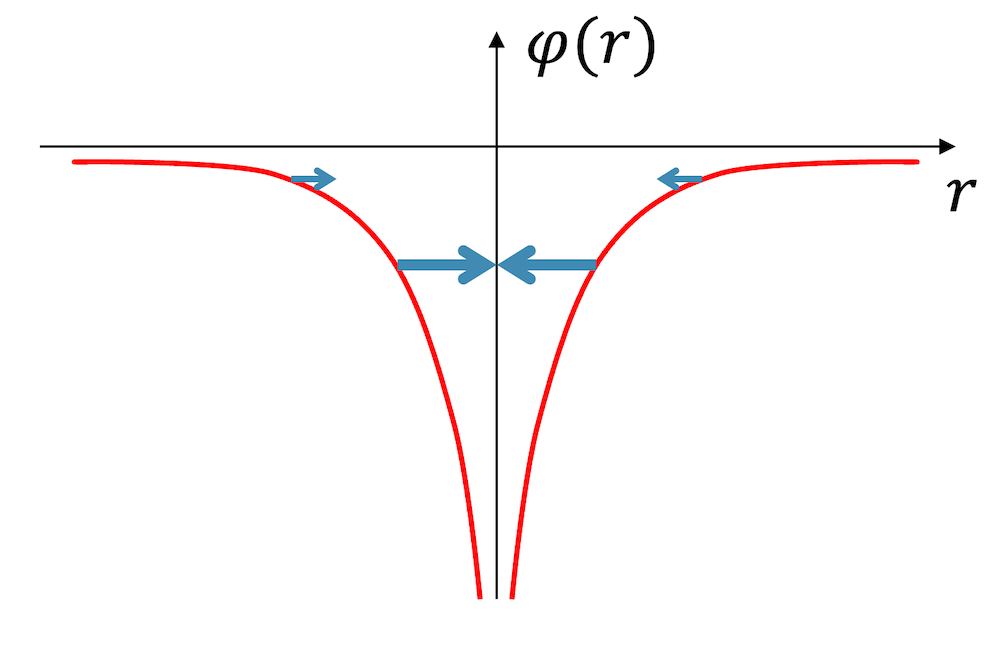
Am Anfang, wenn wir nahe zur negativen Zentralladung sind und unsere Ladung wegziehen, nimmt das Potenzial sehr stark zu. Die Coulombkraft ist sehr gross und wir müssen für jeden Millimeter kämpfen. Dann nimmt aber die Coulombkraft immer mehr ab und es wird immer ringer. Das Potenzial flacht immer mehr ab.

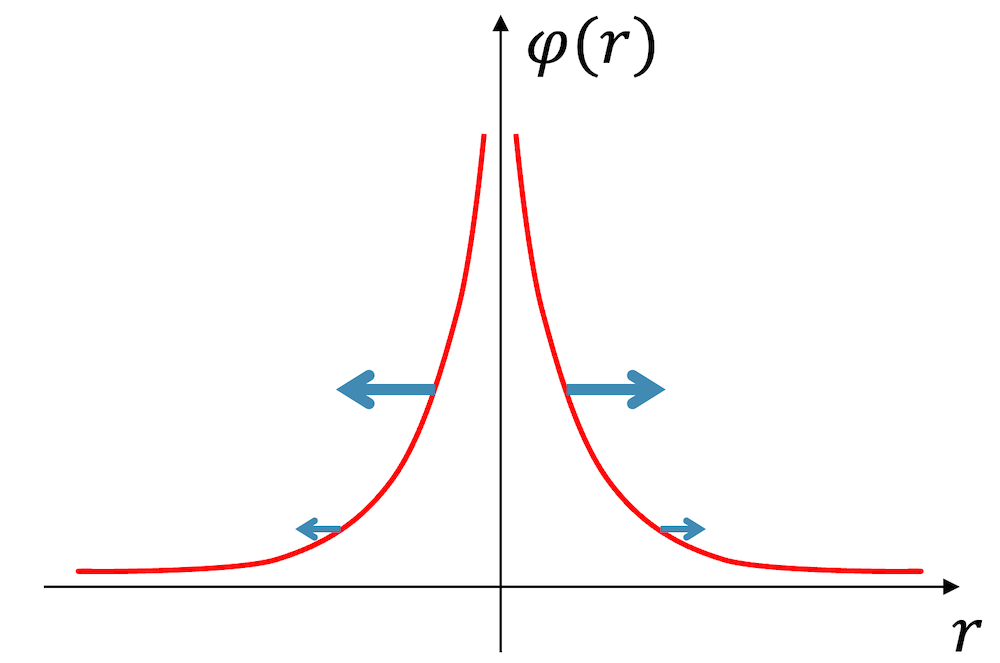
Bei einer positiven Zentralladung ist die Coulomkraft abstossend, d.h. wir müssen die Ladung nicht von der Mitte wegziehen, sondern eher zur Mitte hin stossen. Das elektrische Potenzial ist in diesem Fall gerade umgekehrt. Es nimmt mit kleiner werdendem Abstand zu bzw. mit grösser werdendem Abstand ab (rechts).

Elektrische Spannung als Potenzialdifferenz

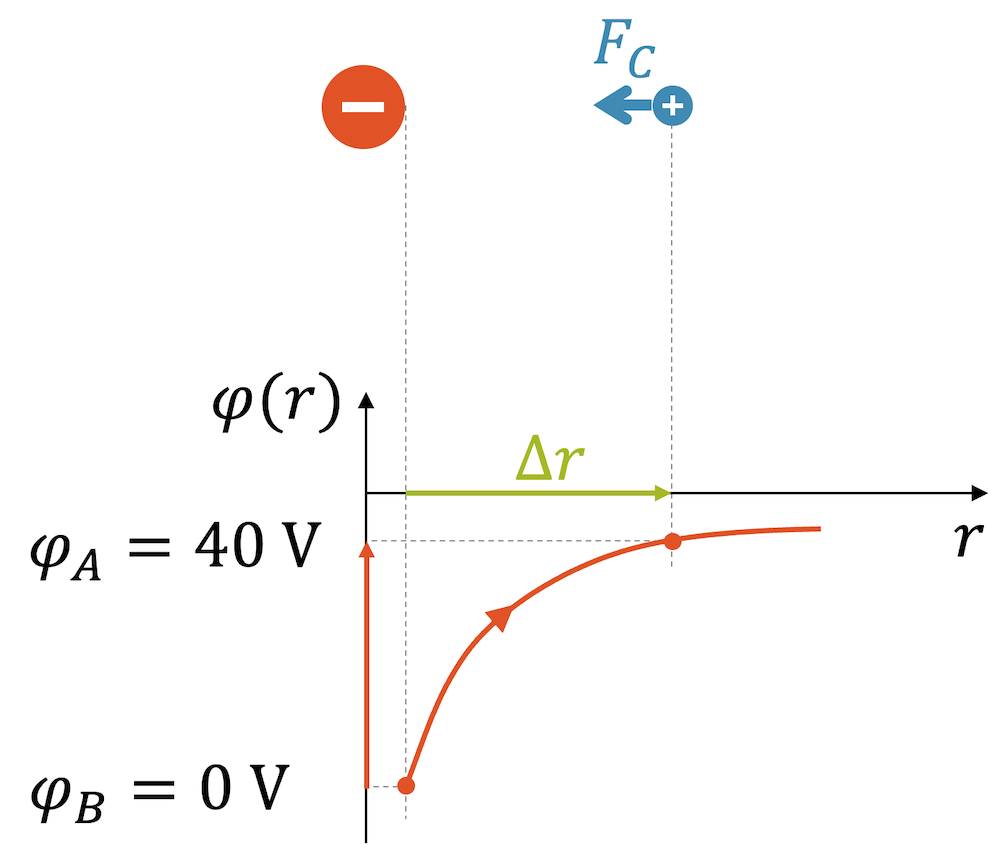
Bisher haben wir elektrische Ladungen ”aufgeladen”, indem wir sie von einer negativen Zentralladung weggezogen haben. Im Potenzialdiagramm sieht das folgendermassen aus: Wir starten beim kleinstmöglichen Abstand und sind da auf einem elektrischen Potenzial von \(\varphi_B=0\,\text{V}\). Dann ziehen wir die Ladung um den Abstand \(\Delta r\) weg und erreichen so das elektrische Potenzial \(\varphi_A=40\,\text{V}\). Die \(40\,\text{V}\) stehen für die Energie, die wir pro Coulomb ”aufgeladen” haben. Die Ladungsmenge \(1\,\text{C}\) hat die Energie \(40\,\text{J}\).

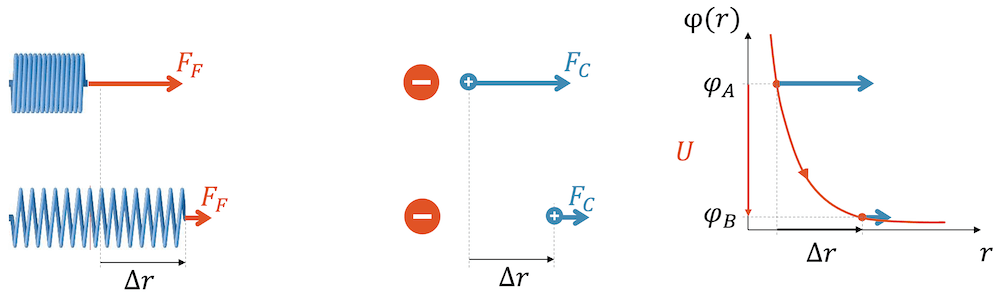
Wir können uns aber auch eine gespannte Feder vorstellen. Wir drücken sie zusammen und ”laden” sie mit Energie. Sobald wir loslassen, gibt die Feder ihre Energie an den kleinen Ball ab (links).

Bei einer positiven elektrischen Ladung drücken wir gegen eine positive Zentralladung. Die Coulombkraft fühlt sich an wie eine Feder, jedoch mit verändernder Federkonstante: Aussen ist die Feder weich. Sobald wir die Ladung aber nahe an die Zentralladung bringen, wird die Feder immer härter.

Auch hier können wir die Ladung näher heranbringen und die unsichtbare ”Coulombfeder” mit Energie aufladen. Sobald wir loslassen, spickt die Ladung durch die Abstossung weg. Die potenzielle Energie der Feder wird in kinetische Energie der Ladung umgewandelt.

Beispiel

Die Ladung \(+0.2\,\text{C}\) wurde um \(\Delta r\) von einer negativen Zentralladung entfernt. Die aufgewendete Arbeit beträgt \(W = 6\,\text{J}\). Wie viel beträgt die Spannung?

---

Wir übernehmen die Definition der Spannung als Differenz zweier elektrischer Potenziale.

\[ U = \varphi_A – \varphi_B = \frac{E_{pot,A}}{q} – \frac{E_{pot,B}}{q} = \frac{\Delta E_{pot}}{q} \]

Jetzt setzen wir für die Energiedifferenz den gegebenen Wert ein.

\[ \Delta E_{pot} = W = 6\,\text{J} \]

Die Spannung entspricht dem Bruch von Energiedifferenz und Ladung:

\[ U = \frac{\Delta E_{pot}}{q} = \frac{6\,\text{J}}{0.2\,\text{C}} = 30\,\text{V} \]