Das elektrische Feld (oft auch als E-Feld abgekürzt) ist die Wirkung einer Ladung im Raum, der sie umgibt. Diese Wirkung zeigt sich mit der Coulombkraft. Die Feldstärke und Richtung wird mit Hilfe einer Testladung von \(+1\) C an allen möglichen Orten im Raum ermittelt. Das E-Feld ist Kraft pro Ladung. Was für \(+1\) C gilt, gilt für andere Ladungen, wenn entsprechend mit ihrem Betrag multipliziert wird:
\[ F_C = E \cdot q \]
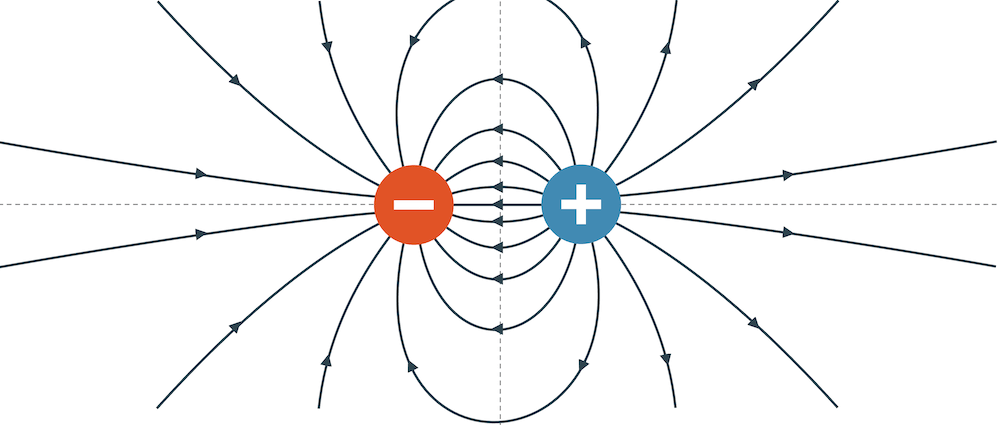
Elektrische Felder werden am besten mit Feldlinien dargestellt. Positive Ladungen erzeugen Quellen von Feldlinien, während negative Ladungen Senken darstellen. Die Feldlinien zeigen die Richtung des Felds und die Feldliniendichte steht stellvertretend für die Stärke des Felds.
Definitionen
Abkürzung: \(\vec{E} \quad\) bzw. \(\quad E\)
Einheit: \([\,E\,] = \frac{\text{N}}{\text{C}} = \frac{\text{V}}{\text{m}}\)
Die Abkürzung \(E\) birgt eine gewisse Verwechslungsgefahr mit der Energie. Wenn elektrische Felder und Energie gleichzeitig vorkommen, bedient man sich gerne der Abkürzung \(W\) (engl. work), die man dann für die Arbeit im elektrischen Feld einsetzt.
Von der Coulombkraft zum elektrischen Feld
Die Coulombkraft ist die Fernwirkung von Ladungen aufeinander. Sie ist auch abhängig vom Abstand zwischen den Ladungen. Was passiert mit der Coulombkraft, wenn wir eine Ladung plötzlich etwas weg bewegen schieben? Eigentlich müsste die andere Ladung dies sofort bemerken, da die Kraft abnimmt, sobald der Abstand grösser wird. Die Information darüber, dass sich eine Ladung bewegt hat, kann nicht //sofort// zur anderen Ladung transportiert werden. Die grösste mögliche Geschwindigkeit in der Physik ist die Lichtgeschwindigkeit, d.h. auch wenn diese unglaublich gross ist, dauert es ein bisschen Zeit, bis die andere Ladung dies mitbekommt.
Hier liegt der Grundgedanke hinter einem Feld, sei es das Gravitationsfeld, das magnetische Feld oder das elektrische Feld. Stellen Sie sich vor, dass alle Ladungen über eine Art ”elastisches Tischtuch” verbunden sind. Wenn eine Ladung sich bewegt, verändert sie das Feld und diese Veränderung breitet sich als Welle auf dem ganzen Tischtuch aus. Beim elektrischen Feld gibt es diese Welle tatsächlich – es ist die elektromagnetische Welle, die im Vakuum mit der Lichtgeschwindigkeit wandert.
Wenn eine Ladung eine Wirkung auf ihre Umgebung hat, so hat sie eine Wirkung auf das elektrische Feld, das sie umgibt. An jeder Stelle im elektrischen Feld tritt die Wirkung in Form einer Coulombkraft zutage. Wenn wir ein elektrisches Feld verstehen möchten, stellen wir uns deshalb vor, welche Wirkung es auf eine Testladung haben, die wir an eine bestimmte Stelle bringen.
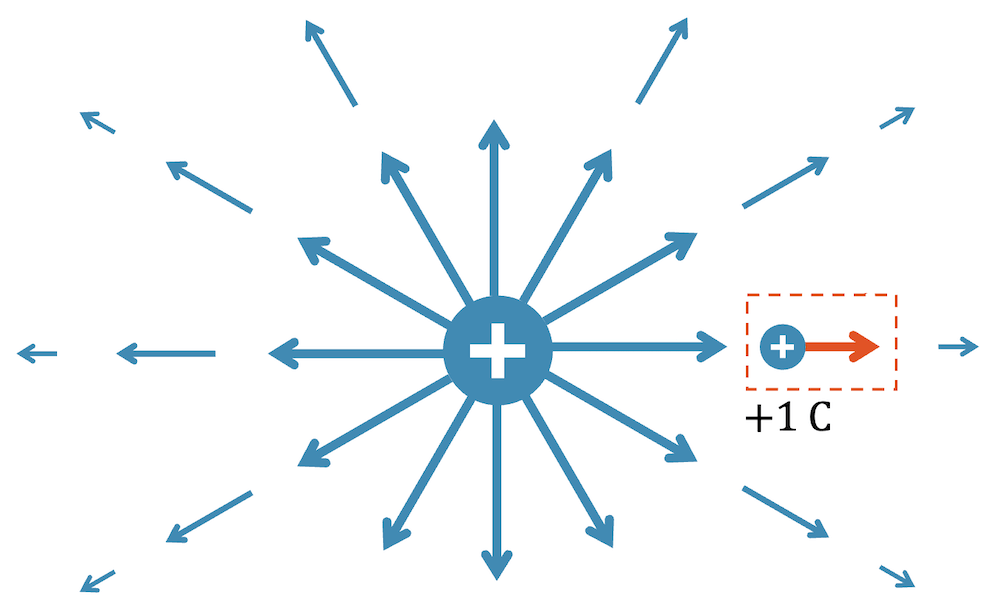
Nehmen wir z.B. eine positive Ladung \(Q\). Ihre Wirkung auf eine Testladung von \(+1\) C ist immer eine abstossende Coulombkraft, weg von ihr gerichtet. Die Stärke der Coulombkraft nimmt mit dem Abstand im Quadrat ab. Zeichnen wir zu fast jeder Position den Vektorpfeil der Coulombkraft, so kriegen wir schnell eine Idee der Wirkung der Ladung \(Q\) auf ihre Umgebung oder anders gesagt: Wir sehen dann, welches elektrische Feld die positive Ladung umgibt (siehe oben).
Wenn wir eine positive Ladung \(q\) irgendwo in das E-Feld der Ladung \(Q\) bringen, wirkt das Feld der Ladung \(Q\) auf die kleine Ladung \(q\). Für die Coulombkraft schreiben wir:
\[ F_C = k \cdot \frac{Q \cdot q}{r^2} = \Big(k \cdot \frac{Q}{r^2} \Big) \cdot q \]
Jetzt nennen wir die Klammer die Stärke des elektrischen Felds \(E = \big(k \cdot \frac{Q}{r^2} \big)\) und erhalten:
\[ F_C = E \cdot q \]
Das elektrische Feld \(E\) ist die Coulombkraft ohne die zweite Ladung: Es ist die Kraft pro Ladung, d.h. wir müssen diesen Wert nur mit der effektiven Ladung \(q\) multiplizieren und erhalten dann die volle Kraft. Die Einheit des E-Felds ist demnach \([ E ] = \frac{\text{N}}{\text{C}}\). Die Richtung der Kraft können wir 1:1 dem Feld entnehmen.
Das ist auch der Grund warum wir immer mit einer Testladung von \(+1\) C rechnen. Der Betrag der Coulombkraft kann direkt als Betrag des Felds übernommen werden. Wenn wir beispielsweise eine Coulombkraft von \(0.8\) N auf eine Testladung von \(+1\) C haben, beträgt die Feldstärke ebenfalls \(0.8\,\frac{\text{N}}{\text{C}}\), weil es ja die Kraft ist pro Coulomb Ladung. Wenn wir jetzt eine Ladung von \(+2\) mC in das gleiche Feld an die gleiche Position mit der Feldstärke \(0.8\,\frac{\text{N}}{\text{C}}\) bringen, beträgt die Coulombkraft einfach \((0.8 \cdot 2)\,\)mN.
Feldlinien
Das Zeichnen des Felds mit den Kraftpfeilen auf eine Testladung von \(+1\) C gibt uns ein gutes Bild der zu erwartenden Coulombkräfte. Da die Kräfte mit dem Quadrat des Abstands abnehmen, werden die Vektorpfeile schnell sehr, sehr kurz und können kaum mehr dargestellt werden. Genauso wird es unpraktisch, wenn die Vektorpfeile zu lange werden.
Statt mit Vektorpfeilen kann das Feld besser mit Feldlinien dargestellt werden: Die Pfeile werden einfach miteinander verbunden, quasi verlängert. Da wir die Pfeile verloren haben, müssen wir hie und da der Feldlinie eine Richtung geben.
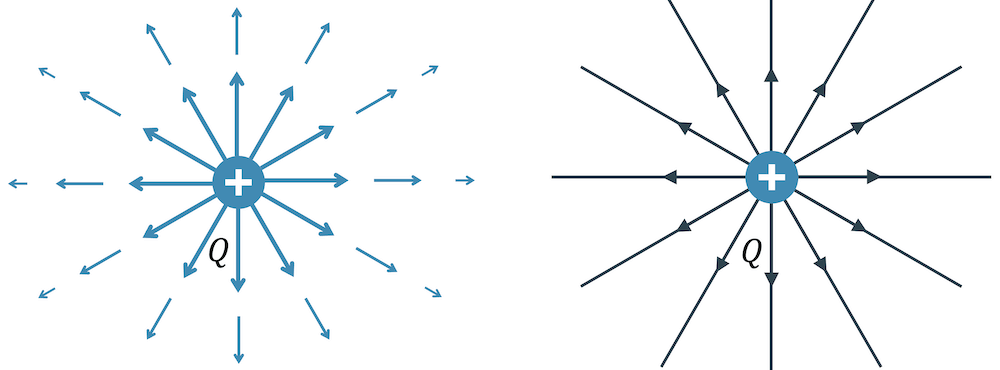
Mit den Vektorpfeilen hatten wir auch ein Indiz für die Stärke des Felds. Mit den Feldlinien scheint diese Information verloren gegangen zu sein. Erstaunlicherweise ist sie das nicht! Die Dichte der Feldlinien gibt uns an, wie stark das Feld ist. Tatsächlich nimmt die Dichte in unserem Beispiel zu, je näher wir der Ladung \(Q\) sind. Weit aussen sind die Feldlinien dieser einen Punktladung so stark verdünnt, dass das E-Feld sehr schwach sein dürfte.
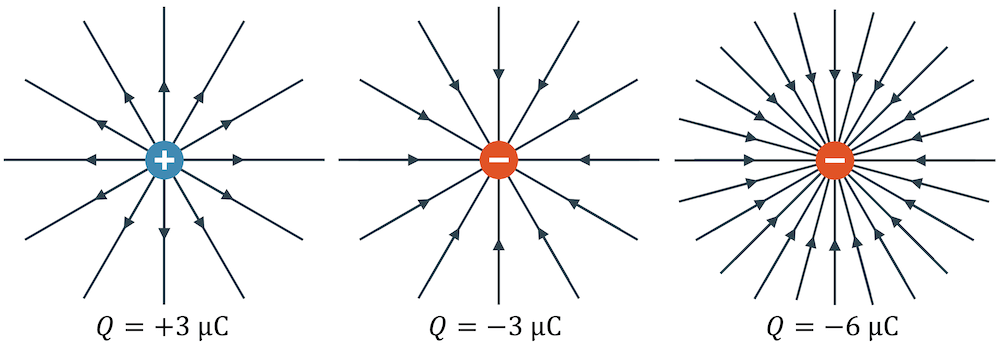
Die obigen drei Beispiele zeigen uns drei verschiedene E-Felder. Das erste E-Feld ist das Feld einer positiven Punktladung \(Q\). Das zweite Feld in der Mitte zeigt ein gleich starkes Feld (gleiche Dichte der Feldlinien), jedoch umgekehrt gerichtet. Es ist das E-Feld einer negativen Punktladung \(Q\). Schliesslich haben wir rechts das E-Feld einer doppelt so starken Punktladung \(Q\) mit einer entsprechend doppelten Dichte an Feldlinien.
Beispiel
Wir haben ein E-Feld von zwei gleichen negativen Punktladungen. Schätze die Feldstärke und -richtung in den Punkten A, B und C ab. Berücksichtige dabei die Kreise gleichen Abstands zu den beiden negativen Ladungen, die das E-Feld erzeugen. Skizziere anschliessend die Feldlinien des ganzen Felds.
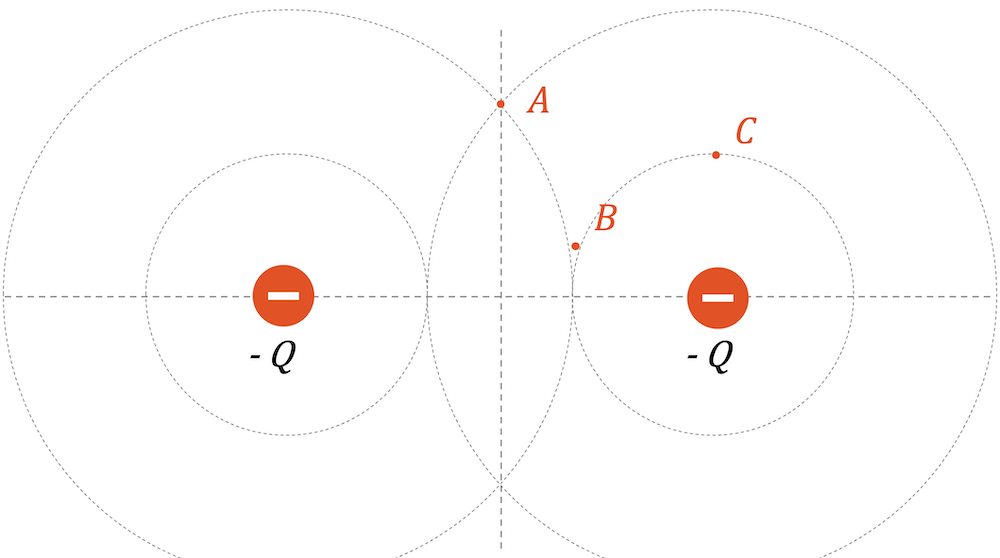
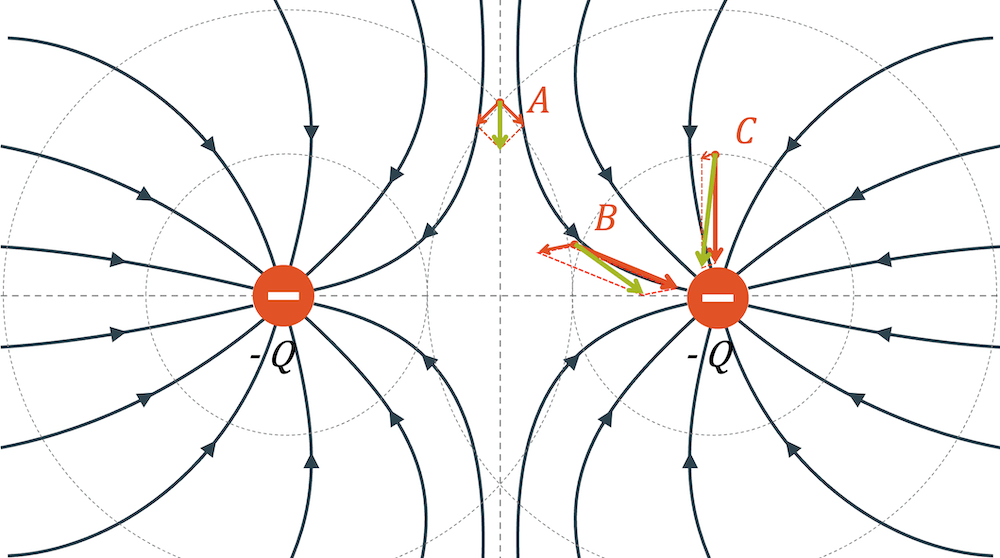
Im Punkt A ist der Abstand zur linken und zur rechten Ladung gleich. Die beiden Coulombkräfte sind gleich gross und zu den beiden Punktladungen gerichtet. Die Summe dieser beiden Kräfte erhalten wir durch Addition der Kraftvektoren. Das Feld zeigt dort senkrecht nach unten und ist noch relativ schwach.
Im Punkt B sind wir immer noch gleich weit zur linken Ladung, jedoch doppelt so nahe zur rechten Ladung. Der Vektor zur linken Ladung ist deshalb gleich lang, der Vektor zur rechten Ladung ist viermal Länger. Wir addieren wieder die beiden Vektoren und erhalten einen längeren Vektor nach rechts unten gerichtet.
Im Punkt C haben wir die gleiche Nähe zur rechten Ladung, sind aber viel weiter zur linken Ladung. Die Summe der beiden Kräfte ergibt eine Feldrichtung, die fast senkrecht nach unten zeigt und nur leicht nach links abgelenkt ist.
Wie sieht das Feld aus, wenn die zwei Punktladungen den gleichen Betrag, jedoch unterschiedliche Vorzeichen haben? Die Kräfte auf der Mittelsenkrechten zwischen den beiden Ladungen haben immer den gleichen Abstand zu den beiden Ladungen. Die Kräfte sind zwar einmal abstossend und einmal anziehend, aber sie sind immer gleich stark, so dass deren Vektorsumme eine horizontale Kraft nach rechts gibt.
Wir erhalten auch hier ein symmetrisches E-Feld, jedoch mit einem deutlichen Unterschied zum E-Feld der beiden gleichen Punktladungen: Hier ”fliessen” die Feldlinien von der positiven zu der negativen Ladung, als wäre die positive Ladung eine Quelle und die negative Ladung eine Senke. Das ”Wasser” fliesst von links nach rechts. Im Falle der gleichen Punktladungen standen die beiden ”Quellen” in gegenseitiger Konkurrenz. Deren Feldlinien prallten aufeinander und flossen in der Unendlichkeit oben und unten ab.
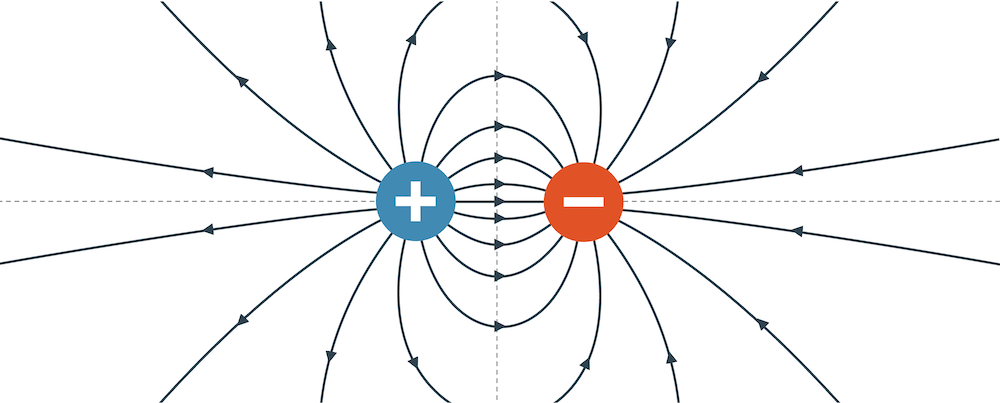
Beachte, dass auch hier die Feldlinien sich nie kreuzen dürfen, denn jeder Punkt im E-Feld hat eine Richtung und darf nicht deren zwei haben! Im Falle einer Kreuzung wär die Richtung der Kraft nicht definiert.
Simulation
https://www.didaktikonline.physik.uni-muenchen.de/programme/e_feld/E_Feld.html
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.