Punkt und Ebene

Punkt auf der Ebene

Mit der folgenden Ebenengleichung erreichen wir alle Punkte \(Q\) auf der Ebene \(E\). Dazu haben wir zwei “Stellschrauben”, die beiden Parameter \(\lambda_1\) und \(\lambda_2\), die sämtliche Werte annehmen können:

\[ \overrightarrow{OQ} \;\; = \;\; \overrightarrow{OA} \; + \; \lambda_1 \cdot \vec{a_1} \; + \; \lambda_2 \cdot \vec{a_2}\]

Jetzt möchten wir aber wissen, ob ein ganz bestimmter Punkt \(P(P_x,P_y)\) auf der Ebene \(E\) ist, oder nicht. Wir nehmen seinen Ortsvektor und setzen ihn mit der Ebenengleichung gleich. Danach lösen wir die Gleichung für \(\lambda_1\) und \(\lambda_2\):

\[ \overrightarrow{OA} \; + \; \lambda_1 \cdot \vec{a_1} \; + \; \lambda_2 \cdot \vec{a_2} \; \stackrel{!}{=} \; \overrightarrow{OP} \quad \rightarrow \quad (\lambda_1,\lambda_2) \]

Mit diesen beiden Parameterwerten erreichen wir den Punkt \(P\).

Gehört ein Punkt \(P\) zur Ebene \(E\), gibt es eine ganz bestimmte Einstellung der beiden Parameter \(\lambda_1\) und \(\lambda_2\), die mit der Ebenengleichung zum Punkt \(P\) führt:

\[ \overrightarrow{OA} \; + \; \lambda_1 \cdot \vec{a_1} \; + \; \lambda_2 \cdot \vec{a_2} \; \stackrel{!}{=} \; \overrightarrow{OP} \]

Diese Vektorgleichung ist ein Gleichungssystem von 3 Gleichungen mit 2 Unbekannten (\(\lambda_1\) und \(\lambda_2\)). Es ist überbestimmt, d.h. zwei Gleichungen reichen für die Bestimmung der Lösung (\(\lambda_1\), \(\lambda_2\)).

\[ \begin{cases} \begin{array}{cc} a_{1,x} \;\lambda_1 + a_{2,x} \;\lambda_2 = OP_x – OA_x \\ a_{1,y} \;\lambda_1 + a_{2,y} \;\lambda_2 = OP_y – OA_y \\ a_{1,z} \;\lambda_1 + a_{2,z} \;\lambda_2 = OP_z – OA_z \end{array} \end{cases} \]

Anschliessend wird die Erfüllung der dritten Gleichung durch die gefundene Lösung (\(\lambda_1\), \(\lambda_2\)) überprüft:

• Erfüllen (\(\lambda_1\), \(\lambda_2\)) die dritte Gleichung ist \(P \in E\)
• Ist die dritte Gleichung durch (\(\lambda_1\), \(\lambda_2\)) nicht erfüllt, gilt \(P \notin E\).

Abstand zwischen Punkt und Ebene

Ist der Punkt \(P\) nicht in der Ebene \(E\), so hat er einen bestimmten Abstand \(d\) zur Ebene \(E\), den wir berechnen können. Wir schauen uns dazu die beiden Punkte \(A \in E\), \(P \notin E\) und die Ebene \(E\) von der Seite an:

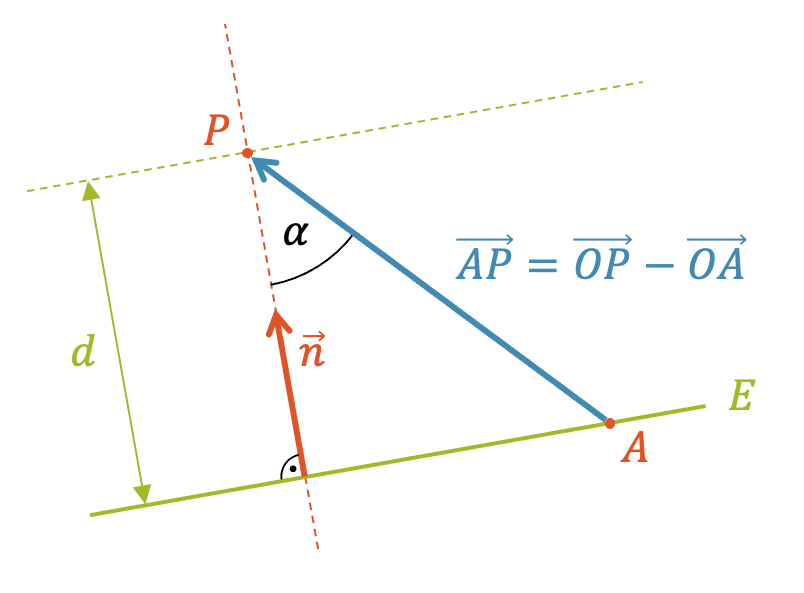
Obwohl es sich um eine räumliche Geschichte handelt, können wir die beiden Punkte \(A\) und \(P\) in unsere Zeichenebene legen. Zuerst legen wir \(P\) in unsere Zeichenebene. Dann legen wir den Normalvektor \(\vec{n}\) der Ebene ebenfalls in unsere Zeichenebene. Schliesslich drehen wir um die Achse (in Richtung von \(\vec{n}\)), bis nun auch der Punkt \(A\) in unserer Zeichenebene liegt.

Wenn \(P\) und \(A\) in der Zeichenebene liegen, dann auch ihr Verbindungsvektor \(\overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}\). Beachte, dass der Ursprung nicht unbedingt in der Zeichenebene sein muss.

Nun berechnen wir den Abstand \(d\) und schauen uns dazu das rechtwinklige Dreieck mit dem Winkel \(\alpha\) an. Wir können die trigonometrische Beziehung zwischen \(d\) und der Hypotenuse aufstellen:

\[ \cos(\alpha) = \frac{d}{\Big|\overrightarrow{AP}\Big|} \]

Für den Kosinus von \(\alpha\) können wir die Beziehung aus dem Skalarprodukt von \(\vec{n}\) und \(\overrightarrow{AP}\) benutzen. Er ist ja der Zwischenwinkel, zwischen den beiden Vektoren:

\[ \cos(\alpha) \;\; = \;\; \frac{\vec{n} \cdot \overrightarrow{AP}}{\big| \vec{n} \big| \cdot \Big|\overrightarrow{AP}\Big|} \]

Wir setzen beides gleich und erhalten eine Gleichung, in welcher wir den einen Betrag weg kürzen können:

\[ \require{cancel} \frac{d}{\cancel{\Big|\overrightarrow{AP}\Big|}} \;\; = \;\; \frac{\Big|\vec{n} \cdot \overrightarrow{AP}\Big|}{\big| \vec{n} \big| \cdot \cancel{\Big|\overrightarrow{AP}\Big|}} \]

Damit haben wir einen Ausdruck für den Abstand \(d\) gefunden. Da das Skalarprodukt im Zähler auch negative Werte erzeugen kann, ein negativer Abstand aber keinen Sinn machen würde, haben wir das Skalarprodukt zwischen zwei Betragsstriche gesetzt. 

Der Abstand \(d\) eines Punktes \(P\) von einer Ebene \(E\) (mit Normalvektor \(\vec{n}\)) kann berechnet werden, wenn ein Punkt der Ebene \(A \in E\) bekannt ist:

\[ d \;\; = \;\; \frac{\Big|\vec{n} \cdot \overrightarrow{AP}\Big|}{\big| \vec{n} \big|} \]