Das Wichtigste in Kürze
Der Lotfusspunkt \(Q\) ist gewissermassen der senkrechte Schatten auf einer Ebene \(E\), der von einem Punkt \(P\) ausserhalb einer Ebene geworfen wird.
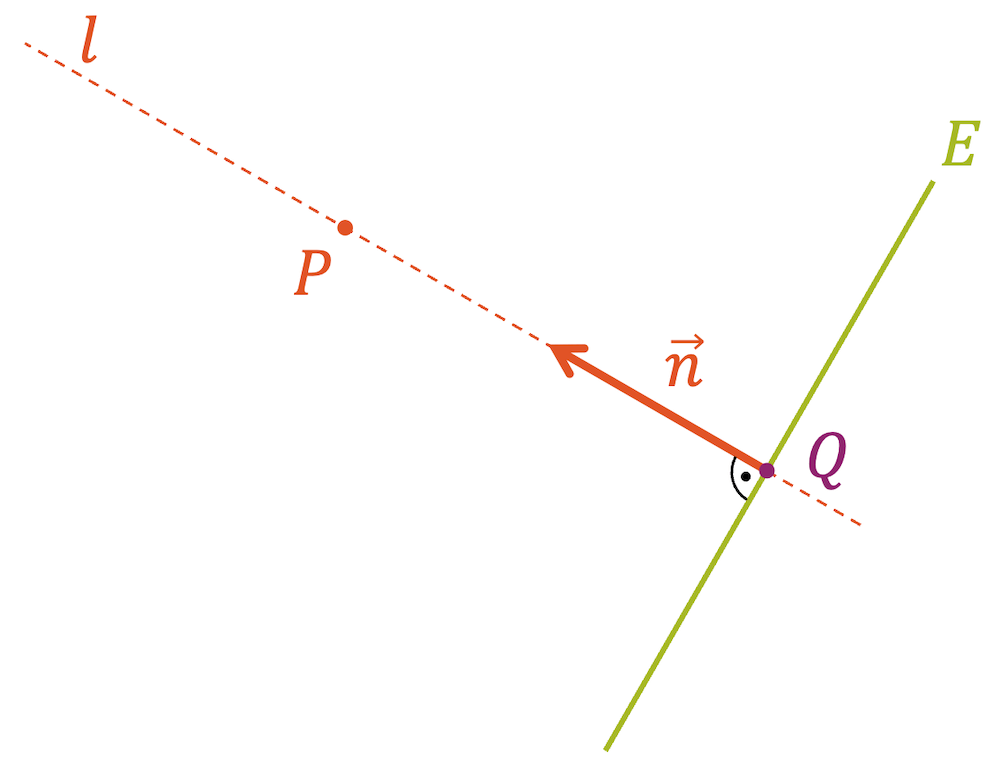
Der Lotfusspunkt wird als Schnittpunkt der Lotgeraden \(l\) mit der Ebene \(E\) erhalten. Die Lotgerade \(l\) entsteht durch aus dem Punkt \(P\) als Stützpunkt und dem Normalvektor \(\vec{n}\) auf der Ebene als Richtungsvektor.
Videos
Unter dem Lotfusspunkt verstehen wir den Punkt auf einer Ebene, in welchem das Lot auf der Ebene auftrifft. Im dargestellten Beispiel ist geht die Lotgerade \(l\) durch den Punkt \(P\) und trifft auf die Ebene im Punkt \(Q\) auf, d.h. \(Q\) ist der Lotfusspunkt von \(P\) auf \(E\).
Beispiel: Lotfusspunkt bestimmen
Finde den Lotfusspunkt \(Q\) von \(P(2,3,2)\) auf \(E\), d.h. den Punkt, der durch das Lot von \(P\) auf \(E\) entsteht.
\[ E \colon \;\; 2x – y – 3z = 9 \]
Der Lotfusspunkt \(Q\) eines Punkts \(P\), der ausserhalb der Ebene \(E\) liegt, ist der Durchstosspunkt der Lotgeraden \(l\) durch \(E\). Die Lotgerade verläuft durch den Punkt \(P\) und hat den Normalvektor von \(E\) als Richtungsvektor.
\[ P \in l, \;\; P \notin E, \;\; l \perp E \quad \rightarrow \quad l \cap E = \big\{Q\big\} \]
Aufgabensammlung
Lernziele
- Du kannst von einem Punkt ausserhalb der Ebene, dessen Lotfusspunkt auf der Ebene bestimmen
Weitere Links
Lot (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.