Das Wichtigste in Kürze
Mit Linearkombinationen der zwei Einheitsvektoren \(\vec{e}_x\) und \(\vec{e}_y\) erreichen wir alle Punkte der \(x,y\)-Ebene:
\[ P(x,y) \quad \rightarrow \quad \overrightarrow{0P} \;\; = \;\; x \cdot \vec{e}_x + y \cdot \vec{e}_y \]
\[ = \;\; x \cdot \begin{pmatrix}1 \\ 0\end{pmatrix} + y \cdot \begin{pmatrix}0 \\ 1\end{pmatrix} \]
Die Vektoren \(\vec{e}_x\) und \(\vec{e}_y\) spannen die \(x,y\)-Ebene auf.
Videos
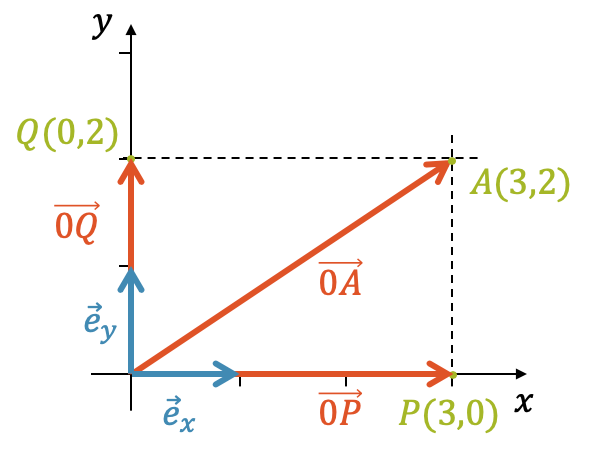
Wir betrachten zuerst den Punkt \(P(0,3)\). Er liegt auf der \(x\)-Achse. Wie kommen wir vom Ursprung zu diesem Punkt mit dem Einheitsvektor \(\vec{e}_x\)?
\[ k \cdot \vec{e}_x = \overrightarrow{0P} \quad \rightarrow \quad k \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 3 \\ 0 \end{pmatrix} \]
\[ \rightarrow \quad k=3 \]
Wir benutzen den dreifachen Einheitsvektor und sind dann am Ziel. Jetzt wiederholen wir das Prozedere und überlegen uns, wie wir mit dem Einheitsvektor \(\vec{e}_y\) vom Ursprung zum Punkt \(Q(2,0)\) gelangen.
\[ l \cdot \vec{e}_y = \overrightarrow{0Q} \quad \rightarrow \quad l \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \end{pmatrix} \]
\[ \rightarrow \quad l=2 \]
Hier brauchen wir einfach den doppelten Einheitsvektor. Wie kommen wir vom Ursprung zum Punkt \(A(3,2)\)? Mit dem Einheitsvektor \(\vec{e}_x\) alleine, können wir uns nur auf der \(x\)-Achse bewegen. Genauso wäre es nicht möglich, nur mit dem Einheitsvektor \(\vec{e}_y\) den Punkt \(A\) zu erreichen. Wir müssen die beiden Einheitsvektoren kombinieren.
\[ \overrightarrow{0A} \;\; = \;\; k \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + l \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} \]
\[ = \;\; \begin{pmatrix} 3 \\ 2 \end{pmatrix} \]
Wir kriegen:
\[ 3 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} \;\; = \;\; \begin{pmatrix} 3 \\ 2 \end{pmatrix} \]
Wir erreichen den Punkt \(A\) mit einer Linearkombination der beiden Einheitsvektoren \(\vec{e}_x\) und \(\vec{e}_y\):
\[ \overrightarrow{0A} = 3 \cdot \vec{e}_x + 2 \cdot \vec{e}_y \]
Es dürfte klar sein, dass wir beispielsweise den Punkt \(B(7,12)\) mit \(\overrightarrow{0B} = 7 \cdot \vec{e}_x + 12 \cdot \vec{e}_y\) erreichen können. Wir können sogar jeden Punkt in der \(x,y\)-Ebene mit Hilfe einer Linearkombination von \(\vec{e}_x\) und \(\vec{e}_y\) erreichen.
Aus diesem Grund sagt man auch, dass die beiden Vektoren \(\vec{e}_x\) und \(\vec{e}_y\) die \(x,y\)-Ebene aufspannen.
Mit Linearkombinationen der zwei Einheitsvektoren \(\vec{e}_x\) und \(\vec{e}_y\) erreichen wir alle Punkte der \(x,y\)-Ebene:
\[ P(x,y) \quad \rightarrow \quad \overrightarrow{0P} \;\; = \;\; x \cdot \vec{e}_x + y \cdot \vec{e}_y \]
\[ = \;\; x \cdot \begin{pmatrix}1 \\ 0\end{pmatrix} + y \cdot \begin{pmatrix}0 \\ 1\end{pmatrix} \]
Die Vektoren \(\vec{e}_x\) und \(\vec{e}_y\) spannen die \(x,y\)-Ebene auf.
Beispiel
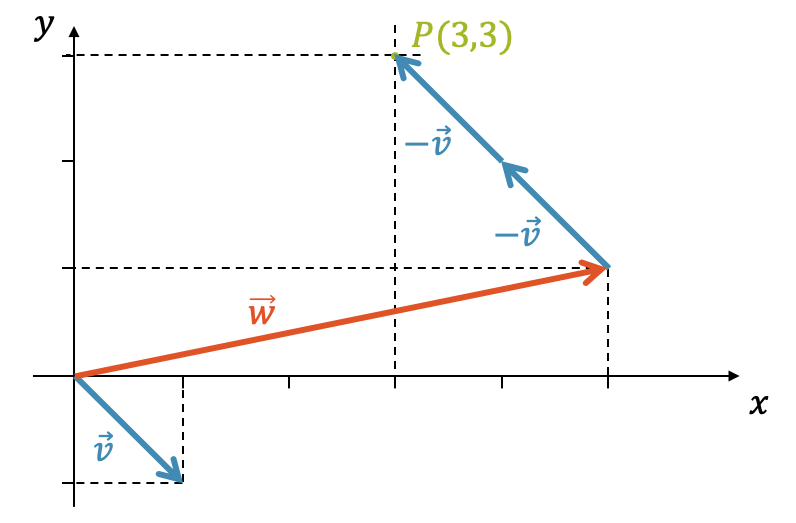
Finde die Linearkombination der beiden Vektoren \(\vec{v}\) und \(\vec{w}\), die den Ortsvektor \(\overrightarrow{0P}\) von \(P(3,3)\) bilden.
\[ \vec{v}=\begin{pmatrix}1\\-1\end{pmatrix}, \quad \vec{w}=\begin{pmatrix}5\\1\end{pmatrix} \]
Beispiel
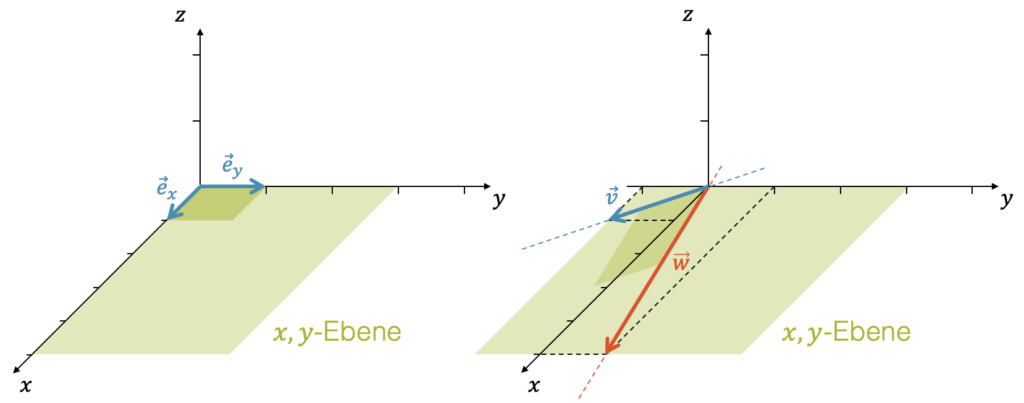
Mit welcher Linearkombination von \(\vec{v}=\begin{pmatrix}1\\-1\end{pmatrix}\) und \(\vec{t}=\begin{pmatrix}-3\\3\end{pmatrix}\) erhalten wir \(\overrightarrow{0P} = \begin{pmatrix}3 \\ 3 \end{pmatrix}\)?
Zwei kollineare Vektoren heissen linear abhängig. Sie spannen keine Ebene auf.
Aufgabensammlung
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.







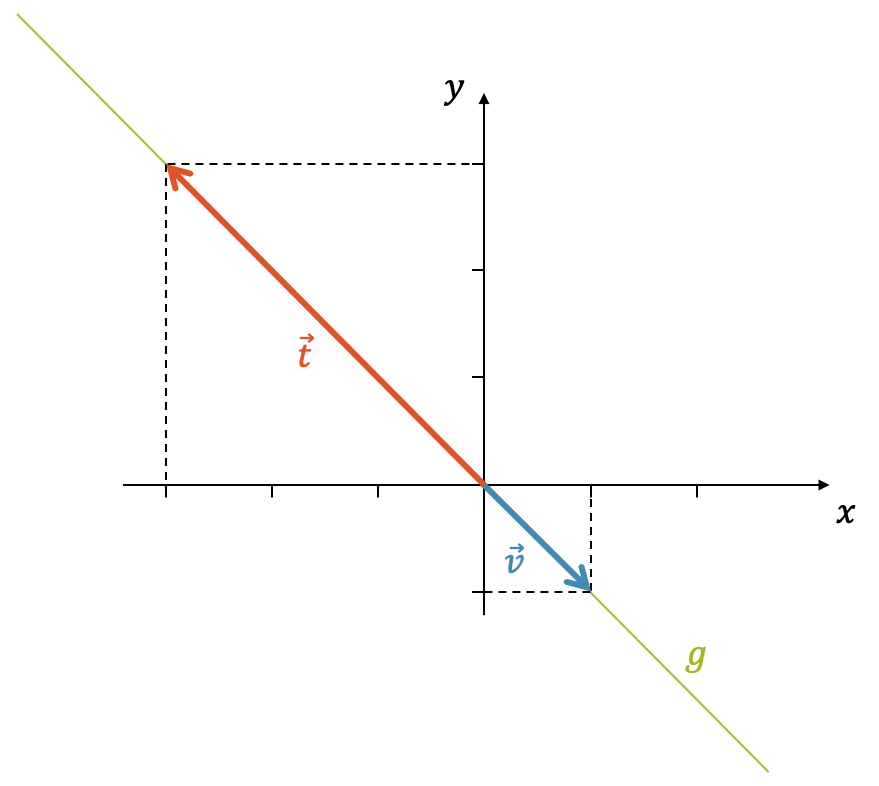



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.