Inhalt
Tutorial Videos
(Es gibt leider keine Tutorial Videos zu diesem Thema)
Wir wissen, dass in einem Zufallsexperiment gewisse Ergebnisse möglich sind, andere nicht. Die möglichen Ergebnisse sind Elemente des Ergebnisraums \(\Omega\), der Menge aller möglichen Ergebnisse \(\omega_i\). Sehr oft sind wir an eine Wahrscheinlichkeit interessiert, für die mehrere Ergebnisse in Frage kommen. Beispielsweise interessiert uns die Wahrscheinlichkeit, mit einem Würfel eine gerade Zahl zu werfen. Die Menge \(E\) mit den dafür gültigen Ergebnissen ist dann eine Untermenge des Ergebnisraums \(\Omega\):
\[ E = \Big\{ 2, 4, 6 \Big\} \;\; \subset \;\; \Omega \]
An dieser Stelle möchte ich noch anmerken, dass der Ergebnisraum \(\Omega\) selbst auch eine Teilmenge ist. Er beinhaltet alle möglichen Ergebnisse und ist damit die Teilmenge der Gesamtmenge aller Ergebnisse überhaupt. Es gibt ja noch die unmöglichen Ergebnisse, die wir uns zwar ausdenken können, die aber im Zufallsexperiment niemals auftreten werden.
Mehrere Ergebnisse können zu einem Ereignis zusammengefasst werden. Unter Ereignis bzw. Ereignismenge wird eine Menge von gültigen Ergebnissen verstanden, die ein bestimmtes Kriterium erfüllen. Die Ereignismenge \(E\) ist immer eine Teilmenge des Ergebnisraums:
\[ E \subset \Omega \]
Ereignisse mit nur einem Ergebnis heissen Elementarereignisse, da sie nicht weiter unterteilt werden können:
\[ E_i = \big\{ \omega_i \big\} \]
Zu einem Ereignis \(A\) gibt es auch das sog. Komplement oder Gegenereignis von \(A\), das wir mit einem Querstrich markieren. Es ist die Menge aller möglichen Ergebnisse, die \(A\) nicht erfüllen, also alle möglichen Ergebnisse (ganzer Ergebnisraum \(\Omega\)) ohne (\(\setminus\)) die Menge der Ergebnisse, die \(A\) erfüllt:
\[ \overline{A} = \Omega \setminus A \]
Unter dem Gegenereignis \(\overline{A}\) von \(A\) verstehen wir die Menge aller Ergebnisse, die \(A\) nicht erfüllen:
\[ \overline{A} = \Omega \setminus A \]
Das Gegenereignis vom Gegenereignis ist wieder das Ereignis selbst:
\[ \overline{\big(\;\overline{A}\;\big)} = A \]
Darstellung mit Diagrammen
Für die Stochastik ist die Mengenlehre sehr praktisch, denn wir können mit ihrer Hilfe eine gute Übersicht über unsere Ereignismengen behalten. In der folgenden Grafik haben wir Ergebnisräume \(\Omega\) und verschiedene Ereignismengen als sog. Venn-Diagramme aufgezeichnet.
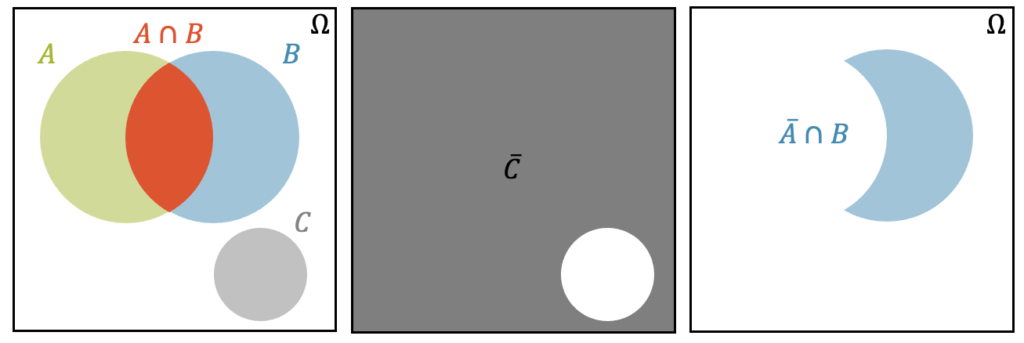
Links sehen wir den Ergebnisraum \(\Omega\) und drei Ereignismengen \(A\), \(B\) und \(C\). Wir sehen auch, dass sich die Ereignismengen \(A\) und \(B\) überschneiden, d.h. es gibt Ergebnisse, die Elemente der beiden Mengen sind. Die rot markierte Teilmenge ist die Schnittmenge von \(A\) und \(B\):
\[ A \cap B \]
Die Mengen \(A\) und \(C\) einerseits und \(B\) und \(C\) andererseits haben keine gemeinsame Schnittmengen. Man nennt Mengen, die sich nicht schneiden, keine gemeinsamen Ergebnisse teilen oder eben eine leere Schnittmenge haben disjunkte Mengen:
\[ A \cap C = B \cap C = \big\{\;\big\} \]
In der Mitte sehen wir das grau markierte Gegenereignis von \(C\), das wir mit einem Querstrich markieren. Es ist die Menge aller möglichen Ergebnisse, jedoch ohne die Ergebnisse von \(C\), die ausgeschlossen sein sollen.
Wenn wir nun statt \(A\), die Menge \(\overline{A}\) mit \(B\) schneiden (drittes Bild), erhalten wir die Menge aller Ergebnisse, die in \(B\) sind, jedoch nicht in \(A\): “B ohne A”.
Unter Schnittmenge verstehen wir die gemeinsame Teilmenge zweier Mengen \(A\) und \(B\). Sie enthält die Ergebnisse, die sowohl \(A\) als auch \(B\) erfüllen:
\[ A \cap B \]
Ist die Schnittmenge eine leere Menge (\(A \cap B = \{ \; \}\)), weil sich \(A\) und \(B\) nicht schneiden bzw. keine gemeinsamen Ergebnisse beinhalten, dann nennt man die beiden Mengen \(A\) und \(B\) disjunkt.
Elementarereignisse beinhalten nur je ein Ergebnis und können deshalb keine Schnittmenge mit anderen Elementarereignissen haben. Sie sind immer disjunkt:
\[ E_i \cap E_j = \{ \omega_i \} \cap \{ \omega_j \} = \{ \; \} \quad \quad (i \neq j) \]
Eine zweite Art von Diagrammen benutzt eine Tabellenform. Die beiden Situationen 2 und 3 können wir mit Hilfe einer Tabelle, manchmal auch Vierfeldertafel genannt, darstellen. Der Vorteil ist eine klare Aufteilung der verschiedenen Schnittmengen.
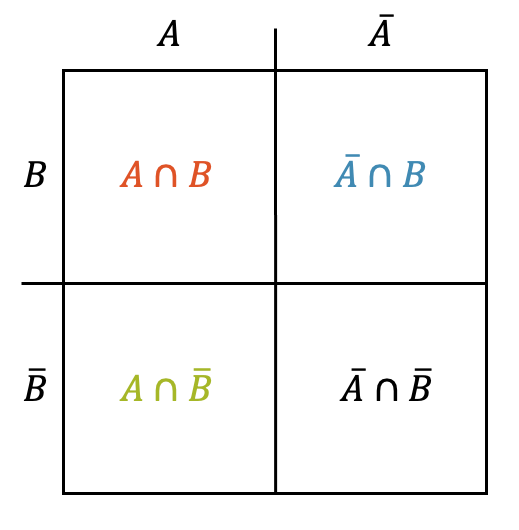
Sobald wir jedoch drei Mengen haben, wird die Darstellung etwas schwieriger zu lesen und für mehr Mengen ist sie komplett ungeeignet. Eine Darstellung für drei Mengen wird im nachfolgenden Beispiel gezeigt.
Beispiel
Stelle für ein Würfelexperiment mit zwei Würfeln die folgenden Ereignisse mit Hilfe eines Venn-Diagramms und einer Mehrfeldtafel grafisch dar:
- Ereignis \(A\) = Die Würfelsumme ist kleiner als 5
- Ereignis \(B\) = Beide Augenzahlen sind gerade
- Ereignis \(C\) = Die Würfelsumme ist eine Dreierzahl
Zuerst müssen wir uns einig sein darüber, was eigentlich die Elementarereignisse sind. Sind es die Würfelsummen oder die einzelnen Augenzahlen?
Für die Ereignisse \(A\) und \(C\) würde die Würfelsumme als Elementarereignis ausreichen. Das Ereignis \(B\) könnte mit einer Summe aber nichts anfangen, denn beiden Augenzahlen müssen bekannt sein. Die Ereignisse \(A\) und \(C\) können mit den beiden Augenzahlen sehr einfach ihre Würfelsumme bilden. Wir einigen uns deshalb auf das Elementarereignis “Augenzahl des ersten Würfels” und “Augenzahl des zweiten Würfels”. Die Reihenfolge kommt nicht darauf an. Wenn wir eine 1 und dann eine 2 würfeln, ist es gleich wie wenn wir zuerst eine 2 und erst mit dem zweiten Würfel eine 1 erhalten:
\[ \{1,2\} \; = \; \{2,1\} \]
Als nächstes machen wir eine Tabelle mit allen möglichen Elementarereignissen und setzen immer ein Kreuz, wenn die Bedingung für das entsprechende Ereignis \(A\), \(B\) oder \(C\) erfüllt ist. Die Schnittmenge \(\overline{A} \cap \overline{B} \cap \overline{C}\) steht für alle Elementarereignis, die weder \(A\), \(B\), noch \(C\) erfüllen:
| Nr. | Elementarereignis | \(A\) | \(B\) | \(C\) | \(\overline{A} \cap \overline{B} \cap \overline{C}\) |
| 1 | \(\{1,1\}\) | X | |||
| 2 | \(\{1,2\}\) | X | X | ||
| 3 | \(\{1,3\}\) | X | |||
| 4 | \(\{1,4\}\) | X | |||
| 5 | \(\{1,5\}\) | X | |||
| 6 | \(\{1,6\}\) | X | |||
| 7 | \(\{2,2\}\) | X | X | ||
| 8 | \(\{2,3\}\) | X | |||
| 9 | \(\{2,4\}\) | X | X | ||
| 10 | \(\{2,5\}\) | X | |||
| 11 | \(\{2,6\}\) | X | |||
| 12 | \(\{3,3\}\) | X | |||
| 13 | \(\{3,4\}\) | X | |||
| 14 | \(\{3,5\}\) | X | |||
| 15 | \(\{3,6\}\) | X | |||
| 16 | \(\{4,4\}\) | X | |||
| 17 | \(\{4,5\}\) | X | |||
| 18 | \(\{4,6\}\) | X | |||
| 19 | \(\{5,5\}\) | X | |||
| 20 | \(\{5,6\}\) | X | |||
| 21 | \(\{6,6\}\) | X | X |
Die Ergebnisse der Tabelle können jetzt einfach in ein Venn-Diagramm eingefüllt werden. Immer wenn für ein Elementarereignis zwei Ereignisse (oder mehr) erfüllt sind, müssen wir die entsprechende Schnittmenge wählen.
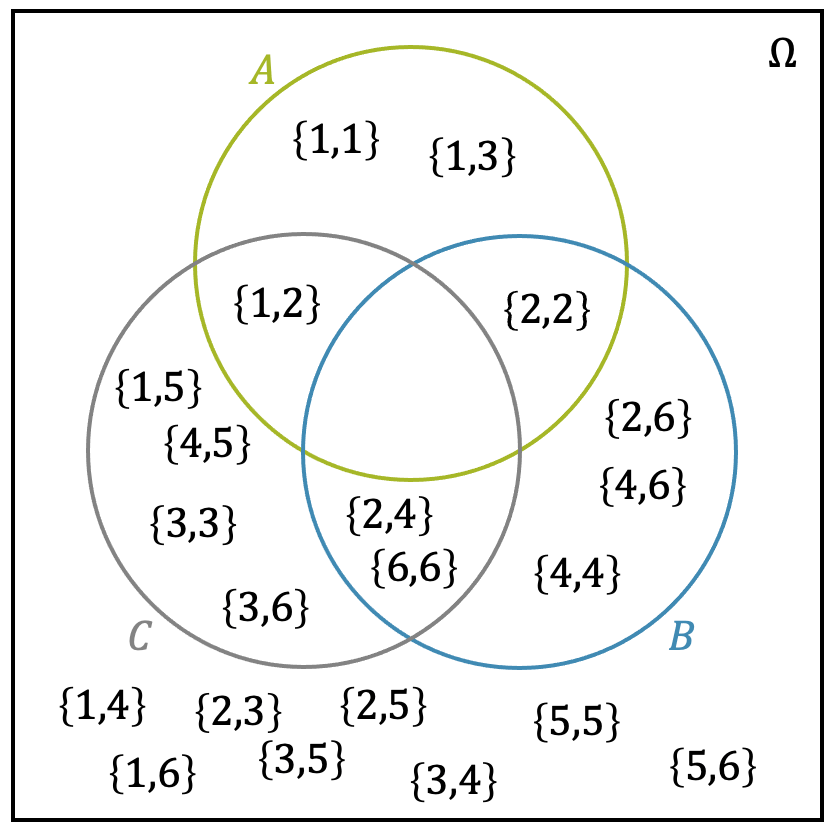
Wir können die Richtigkeit schnell überprüfen, indem wir schauen, ob z.B. die Summe tatsächlich maximal 4 beträgt für die Elementarereignisse in \(A\). In \(B\) sollten nur gerade Augenzahlen stehen, was wir auch mit einem Blick bestätigen können. Schliesslich enthält der Kreis \(C\) alle Elementarereignisse, deren Summe eine Dreierzahl ist. Auch das ist schnell überprüft.
Nachfolgend sind die Elementarereignisse auch in einer Mehrfeldtafel eingesetzt:
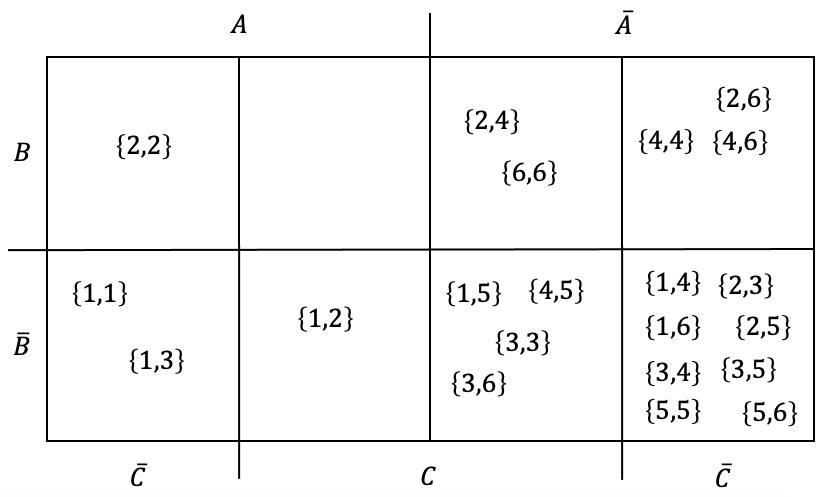
Ereignisse können mit einem Venn-Diagramm dargestellt werden. Pro Ereignismenge wird meist ein rundes Gebiet gezeichnet. Die Schnittmenge zweier Ereignisse entspricht der Überlappung der beiden Gebiete.
Mit einer Vierfeldertafel werden zwei Ereignisse in Form einer Tabelle einander gegenübergestellt. Die vier Felder entsprechen den Schnittmengen der beiden Mengen bzw. derer Gegenereignisse.
Weitere Videos
(keine externe Youtube-Videos zu diesem Thema)
(keine Aufgaben-Videos zu diesem Thema)
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.