Andrei Kolmogorow (1903 – 1987) war ein sowjetischer Mathematiker und einer der bedeutendsten Mathematiker des 20. Jahrhunderts. Mit seinen drei Axiomen haben wir ein Grundgerüst für unsere Arbeit mit der Wahrscheinlichkeit.
Axiom 1 von Kolmogorow
Wenn wir mit \(\Omega\) die Menge aller möglichen Ergebnisse bezeichnen, dann hat ein Ergebnis \(E\) eine bestimmte Wahrscheinlichkeit, die wir mit \(P(E)\) bezeichnen.
Dieser Wahrscheinlichkeit können wir einen Wert zuweisen. Wobei gilt:
- \(P(E)=0\) : Die Wahrscheinlichkeit ist null, d.h. das Ereignis \(E\) kann gar nicht vorkommen
- \(P(E)=1\) : Die Wahrscheinlichkeit ist 1 bzw. 100% und es ist somit garantiert, dass das Ereignis \(E\) eintreffen wird
- \(0 < P(E) < 1\) : Die Wahrscheinlichkeit \(P\) des Ereignisses \(E\) ist irgendwo zwischen 0% (gar nicht möglich) und 100% (garantiert). Das ist natürlich der häufigste Fall.
Kolmogorow stellte mit seinem ersten Axiom fest, dass für alle Ereignisse, die überhaupt möglich sind (und somit Teil der Menge \(\Omega\) sind), die Wahrscheinlichkeit null oder mehr sein kann:
\[ 0 \leq P(E) \leq 1 \quad \forall E \subset \Omega \]
Auf der rechten Seite steht “für alle \((\forall)\) Ereignisse \(E\), die Teilmenge von \(\Omega\) sind.”
Mit diesem Axiom halten wir einfach fest, dass wir mit der Wahrscheinlichkeit \(P\) eine Zahl zwischen 0 und 1 bzw. zwischen 0% und 100% meinen.
Axiom 2 von Kolmogorow
Die Wahrscheinlichkeit, dass das nächste Ereignis, Teil der Menge \(\Omega\) ist und somit stattfindet, ist 100% bzw. 1.
Natürlich muss das so sein, denn die Menge \(\Omega\) beschreibt ja die Menge aller möglichen Ereignisse.
\[ P(\Omega) = 1 \]
Sobald wir uns auf eine Teilmenge davon beschränken, z.B. ein mögliches Ereignis \(E\), ist die Wahrscheinlichkeit zwischen 0% und 100% (Axiom 1):
\[ 0 \leq P(E) \leq 1 \quad \forall E \subset \Omega \]
Beispiel
Wie gross ist die Wahrscheinlichkeit, beim gleichzeitigen Wurf von zwei Münzen, genau “Kopf und Kopf” zu erhalten? Vergleiche mit den Axiomen 1 und 2 von Kolmogorow.
Beispiel
Berechne \(P(\overline{E})\) für den Fall, dass \(P(E) = 80\%\).
Axiom 3 von Kolmogorow
Kolmogorows drittes Axiom betrifft die Wahrscheinlichkeit von unvereinbaren Ereignismengen, die keine gemeinsame Schnittmenge haben bzw. disjunkt sind.
Axiom 3:
\[ P(A \cup B) = P(A) + P(B) \]
für disjunkte Ereignismengen \(A\) und \(B\), d.h.
\[ A \cap B = \{\;\} \]
Beispiel
Zeige mit dem dritten Axiom von Kolmogorow, dass die Wahrscheinlichkeit, eine gerade Zahl zu würfeln, genau 50% entspricht.
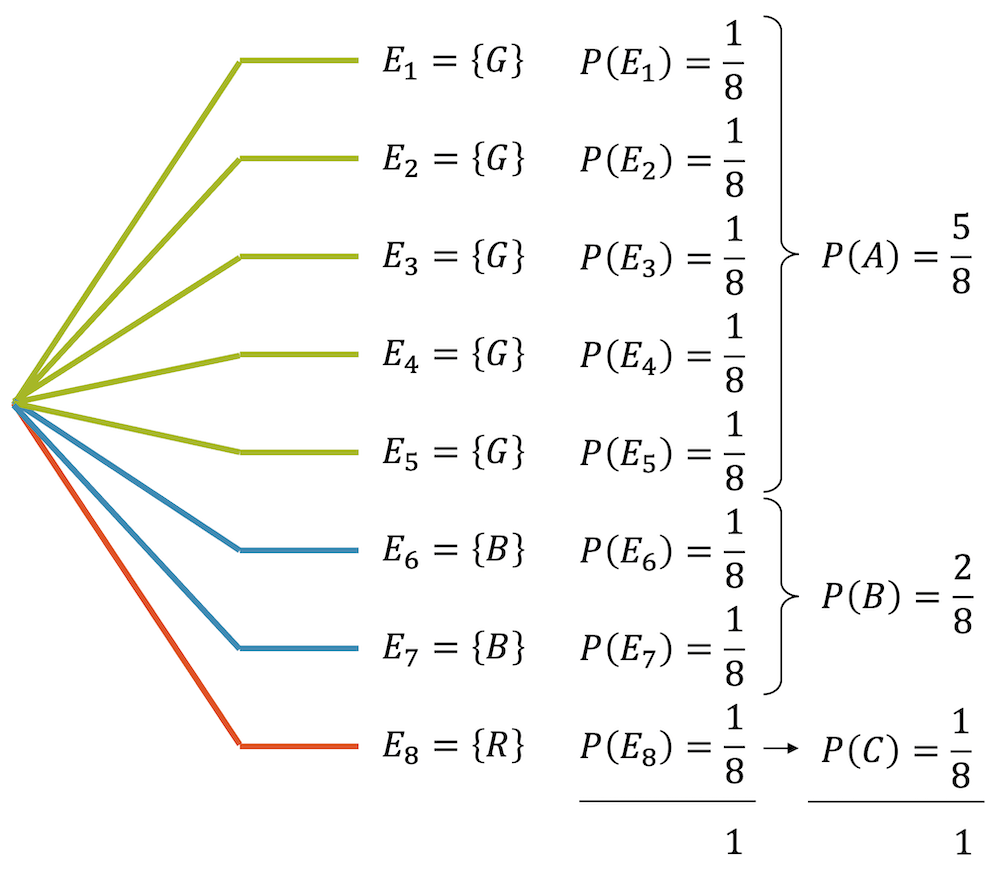
Elementarereignisse \(\{\omega_i\}\) sind immer disjunkt, so dass wir die Wahrscheinlichkeiten von Elementarereignissen immer summieren können:
\[ E = \Big\{\{\omega_1\}, \{\omega_2\}, …, \{\omega_n\}\Big\} \quad \rightarrow \quad P(E) = P(\{\omega_1\}) + P(\{\omega_2\}) + … + P(\{\omega_n\}) \]
Beispiel
Eine Urne enthält 8 Kugeln, eine Kugel ist rot (\(R\)), zwei Kugeln sind blau (\(B\)), die restlichen Kugeln sind grün (\(G\)). Nun wird eine Kugel zufällig gezogen. Mit welcher Wahrscheinlichkeit ist diese grün, blau oder rot?
Ereignisse:
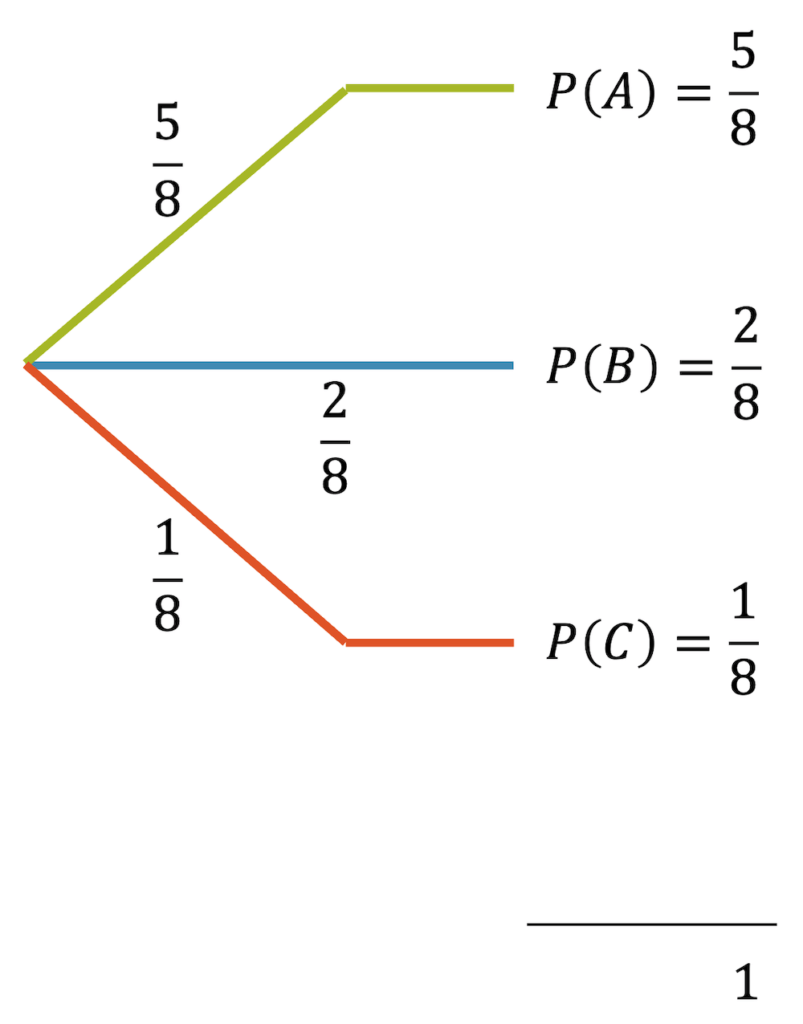
- \(A\) = Die gezogene Kugel ist grün
- \(B\) = Die gezogene Kugel ist blau
- \(C\) = Die gezogene Kugel ist rot
Zeichne einen Ereignisbaum und berechne die Wahrscheinlichkeit mit Hilfe des Axioms 3 von Kolmogorow.
Wir können jede Kugel von 1 bis 8 nummerieren. Das Ziehen der Kugel 1 entspricht dem Elementarereignis \(E_1\). Da wir 8 gleichwertige Kugeln haben, gilt:
\[ P(E_i) = \frac{1}{8} \]
Die ersten fünf Kugeln sind grün, d.h. für das Ereignis \(A\) gilt:
\[ A = E_1 \cup E_2 \cup E_3 \cup E_4 \cup E_5 \]
Da die Elementarereignisse immer disjunkt sind, wie auch hier, können wir Kolmogorow 3 anwenden. Die Wahrscheinlichkeit \(A\) ist die Summe der Wahrscheinlichkeiten der Elementarereignisse \(E_1\) bis \(E_5\):
\[ P(A) = P(E_1) + P(E_2) + P(E_3) + P(E_4) + P(E_5) \]
\[ P(A) = 5 \cdot \frac{1}{8} \; = \; \underline{\frac{5}{8}} \]
Für das Ereignis \(B\), eine blaue Kugel zu ziehen, gilt:
\[ B = E_6 \cup E_7 \]
\[ P(B) = P(E_6) + P(E_7) = \frac{1}{8} + \frac{1}{8} \; = \; \underline{\frac{2}{8}} \]
Schliesslich haben wir für das Ziehen einer roten Kugel \(R\):
\[ R = E_8 \quad \rightarrow \quad P(R) \; = \; \underline{\frac{1}{8}} \]
Die Summe der Wahrscheinlichkeiten sämtlicher Äste eines Ereignisbaums ist 1, wenn dieser Ereignisbaum sämtliche möglichen Fälle abdeckt.
Pfadregel: Die Wahrscheinlichkeit eines Ereignisses, das mehrere Elementarereignisse beinhaltet und somit durch mehrere Pfade erreicht wird, entspricht der Summe der Wahrscheinlichkeiten dieser Elementarereignisse.
Aufgabensammlung
-
Wahrscheinlichkeit (5054) – Aufg. 1
4 Teilaufgaben (pdf/Video-Lösung):
Französisches Roulette (Textaufgabe) -
Wahrscheinlichkeit (5054) – Aufg. 2
5 Teilaufgaben (pdf/Video-Lösung):
Zwei Würfel gleichzeitig geworfen (Textaufgabe) -
Wahrscheinlichkeit (5054) – Aufg. 3
3 Teilaufgaben (pdf/Video-Lösung):
Tombola (Textaufgabe) -
Wahrscheinlichkeit (5054) – Aufg. 4
3 Teilaufgaben (pdf/Video-Lösung):
Zwei Münzen geworfen (Textaufgabe) -
Wahrscheinlichkeit (5054) – Aufg. 5
1 Aufgabe (pdf/Video-Lösung):
Baumdiagramm -
Wahrscheinlichkeit (5054) – Aufg. 6
3 Teilaufgaben (pdf/Video-Lösung):
Bogenschiessen (Textaufgabe)
Lernziele
- Du weisst, dass die Wahrscheinlichkeit ein theoretischer Wert zwischen 0 und 1 ist, der bei einer sehr grossen Anzahl Versuche durch die relative Häufigkeit annähernd erreicht wird.
- Du kennst das dritte Axiom von Kolmogorow und kannst es in eigene Worte fassen. Insbesondere weisst Du, warum dieses Axiom für Elementarereignisse so wichtig ist.
Weitere Links
Wahrscheinlichkeitstheorie – Axiome von Kolmogorov (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.