Anzahl Lösungen von Potenzgleichungen
Gleichungen mit Potenzen, die grösser sind als 2 nennen wir einfach allesamt Potenzgleichungen (streng genommen gehören die linearen und quadratischen Gleichungen eigentlich ja auch zu den Potenzgleichungen, denn sie haben die Potenzen \(x^1\) und \(x^2\)).
Wenn lineare Gleichungen bis zu einer Lösung, quadratische Gleichungen bis zu zwei Lösungen haben, dann liegt der Gedanke nahe, dass Potenzgleichungen die gleiche Anzahl Lösungen haben, wie ihr Grad. Ist das so? Betrachten wir z.B. die folgende Potenzgleichung:
\[ x^3 = 0 \]
Wir können diese Gleichung mit der grafischen Methode darstellen als den Schnittpunkt von \(y_1=x^3\) und \(y_2=0\). Die beiden Kurven schneiden sich in einem Punkt, woraus wir eigentlich nur eine Lösung vermuten würden. Das ist auch nicht ganz falsch. Die einzige Lösung ist \(x=0\), doch sie ist dreifach, denn
\[ x \cdot x \cdot x = 0\]
Jedes der drei \(x\) kann null sein und die Gleichung erfüllen. Es sind eigentlich drei Punkte, die übereinander liegen oder eben eine dreifache Lösung in \(x=0\).
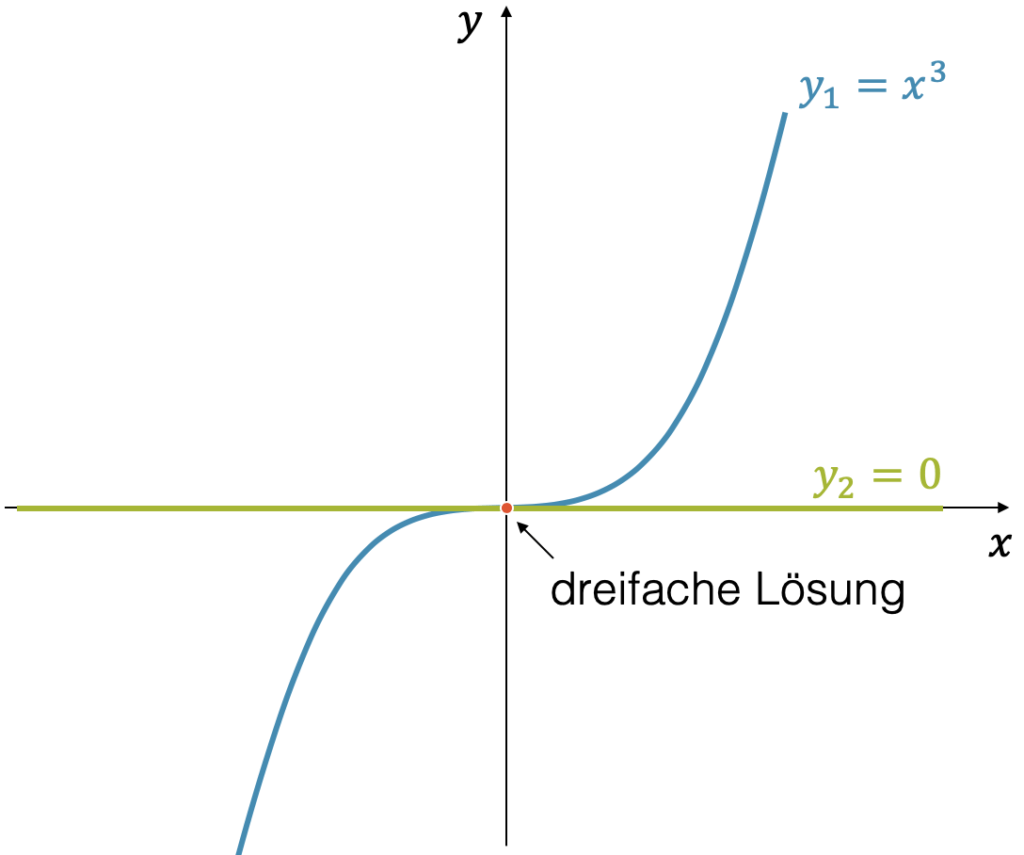
Wir können die dreifache Lösung auch daran erkennen, dass die beiden Kurven sich nicht wie gewohnt schneiden, sondern sich von beiden Seiten asymptotisch annähern.
Wir schauen uns zwei weitere Beispiele an: Die Gleichung \(-x^2=0\) hat eine zweifache Lösung in \(x=0\). Die Parabel nähert sich asymptotisch der horizontalen Geraden an und berührt sie in einem Punkt. Diese Lösung gilt zweifach.
Entsprechend hat die Gleichung \(x^4=0\) eine vierfache Lösung in \(x=0\). Unter Berücksichtigung der mehrfachen Lösungen entspricht die maximale Anzahl von Lösungen tatsächlich dem Grad der Potenz.
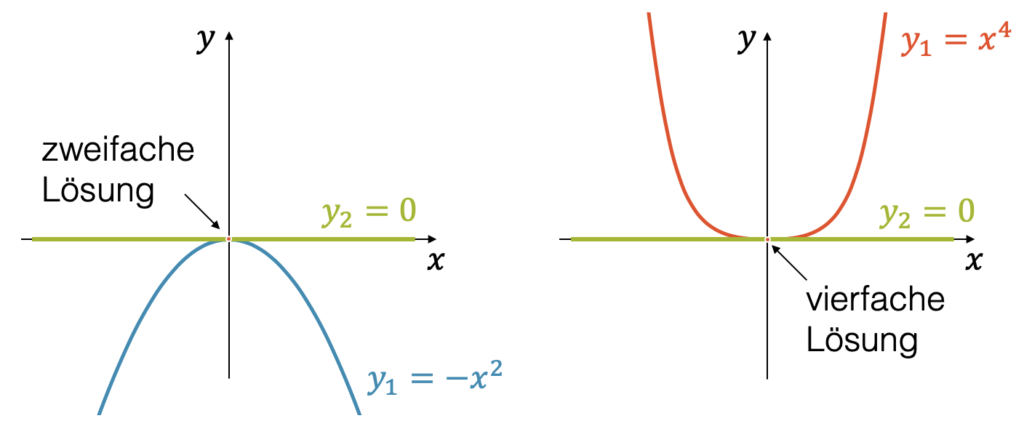
Beispiel
Wie viele Lösungen hat die folgende Gleichung? Stelle sie mit der grafischen Methode dar.
\[ x^3=\frac{1}{2}x \]
Wir erkennen, dass wir beidseitig \(x\) haben, d.h. wir könnten die Gleichung durch \(x\) teilen. Jedoch halt! Das heisst eben auch, dass wir bereits eine Lösung vor uns haben. Setze mal \(x=0\) ein. Was passiert? Die Gleichung ist erfüllt! Null ist bereits eine Lösung für \(x\).
Wir notieren uns die erste Lösung und suchen jetzt die anderen Lösungen, die nicht null sind. Wir schliessen \(x=0\) als Möglichkeit aus und dividieren links und rechts durch \(x\). Eine solche Division ist ja nur unter der Bedingung \(x \neq 0\) erlaubt.
\[ x^2=\frac{1}{2} \]
Jetzt ziehen wir die Wurzel auf beiden Seiten der Gleichung und berücksichtigen, dass die Wurzel von \(\frac{1}{2}\) nur positiv sein kann, denn Wurzeln liefern immer nur positive Werte! Kein Problem. Auf der rechten Seite haben wir \(\sqrt{\frac{1}{2}}\) bzw. \(\frac{1}{\sqrt{2}}\) und das sind definitiv positive Zahlen. Auf der linken Seite gilt \(\sqrt{x^2}>0\), aber wir wissen nicht, ob \(x\) positiv oder negativ ist – beides ist möglich. Deshalb schreiben wir \(+x\) für den Fall, dass \(x>0\) und \(-x\) für den Fall, dass \(x<0\), denn dann ist \((-x)>0\):
\[ \pm \, x=\frac{1}{\sqrt{2}} \]
Wir haben damit links und rechts eine positive Zahl. Im Ganzen haben wir also drei Lösungen erhalten:
\[ \underline{\boldsymbol{L} = \Bigl \{ -\frac{1}{\sqrt{2}}, \,\, 0, \,\, \frac{1}{\sqrt{2}} \Bigr \}} \]
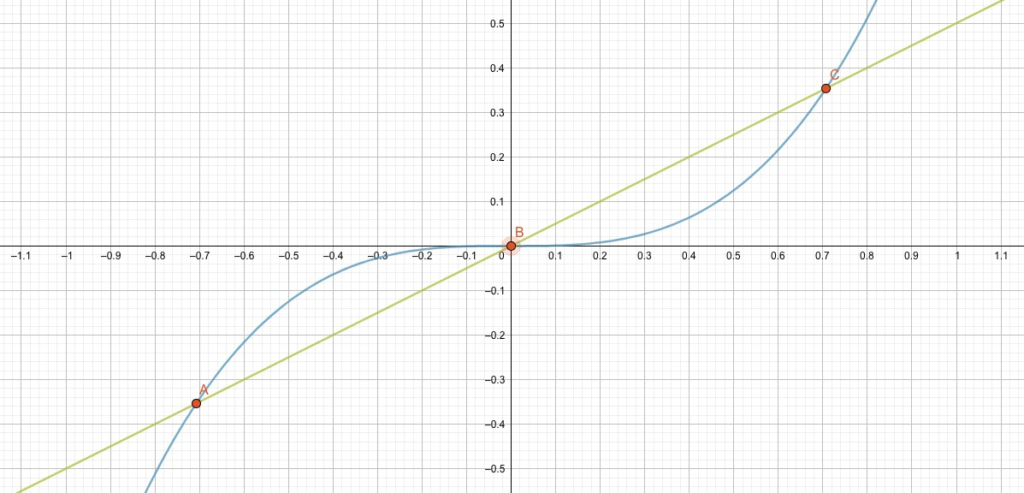
Schaue Dir jetzt die grafische Lösung an. Die Potenzgleichung \(y_1=x^3 \) ist blau, die lineare Gleichung \(y_2=\frac{1}{2}x\) ist grün dargestellt. Sie schneiden sich tatsächlich in den drei Punkten, die unseren drei Lösungen entsprechen.
Beachte auch, dass alle drei Schnittpunkte wirklich einfache Lösungen sind. Selbst der Schnittpunkt in \(x=0\) ist jetzt einfach, weil die beiden Kurven sich schneiden. Es gibt ein Annähern, aber kein asymptotisches Annähern mehr, denn die Asymptote wäre horizontal, die grüne Kurve ist aber schräg.
Potenzgleichungen \(n\)-ten Grades, d.h. deren höchste, vorkommende Potenz \(x^n\) ist, können null bis \(n\) Lösungen für \(x\) haben.
Polynomgleichungen
Polynome sind Summen von Potenzen, d.h. “ein Gemisch” von Potenzen. Deshalb können wir unser Wissen zu den (reinen) Potenzgleichungen auf die etwas weniger “reinen” Polynomgleichungen übertragen. Wir schauen uns dazu ein Beispiel an:
\[ x^4-x^3-13x^2+x+12 = 0 \]
Es geht hier darum, die Nullstellen des Polynoms auf der linken Seite zu finden. Dieses Polynom hat eine höchste Potenz von 4 und ist somit vom Grad 4. Das Polynom ist in der sog. Normalform geschrieben. Um die Nullstellen zu bestimmen, müssen wir dieses Polynom vierten Grades zuerst in die Produktform mit vier Faktoren bringen:
\[ (x-x_1)\cdot(x-x_2)\cdot(x-x_3)\cdot(x-x_4) = 0 \]
Die vier Nullstellen (Lösungen) befinden sich bei \(x_1, x_2, x_3\) und \(x_4\), denn wenn wir für \(x\) z.B. den Wert \(x_1\) einsetzen, ergibt die erste Klammer genau null und somit ist das ganze Produkt null und die Gleichung ist erfüllt. Wie man von der Normalform zur Produktform gelangt, ist nicht immer einfach. Wir nehmen jetzt einfach an, wir hätten dies schon gemacht:
\[ x^4-x^3-13x^2+x+12 \]
\[ = (x+3) \cdot (x+1) \cdot (x-1) \cdot (x-4) \]
\[ = \quad 0 \]
Jetzt muss ein Faktor, d.h. eine Klammer null sein, damit die Gleichung erfüllt ist. Wir haben vier Klammern und somit vier Möglichkeiten, die Gleichung zu erfüllen. Nehmen wir die erste Klammer, so ist sie null, wenn \(x=-3\). Das ist unsere erste Lösung. Auf diese Art erhalten wir die restlichen drei Lösungen und stellen die Lösungsmenge auf:
\[ \boldsymbol{L} = \Bigl \{ -3,\,\,-1,\,\,1,\,\,4\Bigr \} \]
Beachte, dass in der Klammer der Faktoren das Vorzeichen der Zahl immer gerade umgekehrt ist zum Vorzeichen der entsprechenden Lösung. Der Plot des Verlaufs unseres Polynoms ergibt mit dem Computer tatsächlich die gefundenen Nullstellen.
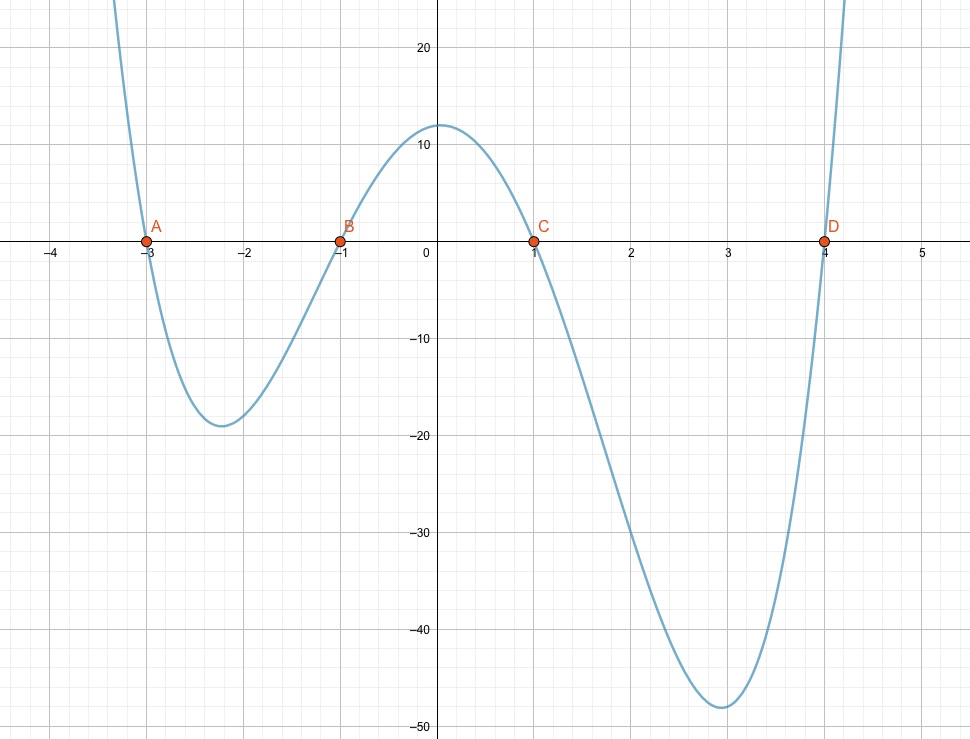
Du erkennst hier auch, dass wir bei einem Polynom vierten Grades so etwas wie eine doppelte Parabel haben, d.h. das Doppelte eines Polynoms zweiten Grades. Beide Äste sind nach oben gerichtet. Die beiden “Parabeln” ergeben zwei Minima, die dazwischen mit einem lokalen Maximum verbunden sind.
Polynomgleichungen \(n\)-ten Grades, d.h. deren höchste, vorkommende Potenz \(x^n\) ist, können null bis \(n\) Lösungen für \(x\) haben.
Es gibt für Polynomgleichungen die Normalform als Summe der Potenzen, typischerweise mit absteigender Potenz:
\[ y(x) = a_n x^n + a_{n-1}x^{n-1} + … + a_2 x^2 + a_1 x + a_0 \]
Sie kann auch geschrieben werden mit der Summenformel:
\[ y(x) = \sum_{k=0}^{n}a_k x^k = 0 \]
Polynomgleichungen können auch in Produktform, d.h. als Produkt von vielen Faktoren \((x-x_k)\) ausgedrückt werden:
\[ y(x) = (x-x_n)(x-x_{n-1})\cdot…\cdot(x-x_2)(x-x_1) \]
Beispiel
Bestimme die Lösungen der Polynomgleichung \(x^2+9x=3x-9\)
Links haben wir ein Polynom 2. Grades (eine Parabel) und rechts ein Polynom 1. Grades (eine gerade Linie). Im Kopf können wir uns deshalb schon vorstellen, dass wir eine Parabel mit einer geraden Linie schneiden und 0, 1 oder 2 Schnittpunkte bzw. Lösungen erhalten werden.
Wir bringen das Polynom zuerst in die Normalform, indem wir die rechte Seite null machen, d.h. wir subtrahieren \(3x\) und addieren 9.
\[ x^2+9x-3x+9=0 \]
\[ x^2+6x+9=0 \]
Jetzt müssen wir das Polynom in seine Faktoren zerlegen, so dass wir die Nullstellen bestimmen können. Bei Polynomen zweiten Grades schauen wir immer gleich, ob wir eine binomische Formel erkennen können. Wir haben Glück und unser Polynom entspricht der binomischen Formel \(a^2+2ab+b^2 = (a+b)^2\), was uns die Produktform liefert, die uns die Nullstellen verrät:
\[ x^2+6x+9 = (x+3)^2 \]
\[ = (x+3) \cdot (x+3) = 0 \]
Die Nullstellen sind “beide” bei \(x=-3\), d.h. im gleichen Punkt, wo die Gerade die Parabel berührt, d.h. es ist eine doppelte Lösung in \(x=-3\):
\[ \underline{\boldsymbol{L} = \Bigl \{ -3 \Bigr \}} \]
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.