Logarithmus

Andere Schreibweise für eine Potenz

Der Logarithmus ist nichts anderes als eine andere Schreibweise für eine Potenz. Warum eine neue Schreibweise? Was bringt das?

Wenn wir Gleichungen lösen, dann ist die Unbekannte meistens in der Basis, z.B. \(x^2\) in einer quadratischen Gleichung. Eine solche Gleichung lösen wir mit einer Wurzel, übrigens ebenfalls eine andere Schreibweise für eine Potenz.

Bei Exponentialfunktionen ist die Unbekannte im Exponenten und wir können sie mit einem Logarithmus.

\[ a^b = x \quad \leftrightarrow \quad \log_a(x) = b \]

Wir lesen den Logarithmus wie folgt:

Auch wenn es am Anfang etwas komisch ist, gewöhnt man sich relativ schnell daran.

Aufgrund der Eigenschaften von Potenzen, kriegen wir folgende Identität, gültig für jede Basis \(a\):

\[ \log_a(1) = 0 \]

Diese Identität folgt direkt daraus, dass \(a^0 = 1\), egal wie gross \(a\) ist.

Aus \(a^1=a\) folgt die nächste Identität:

\[ \log_a(a) = 1 \]

Damit wissen wir, dass der Logarithmus von 1 immer null ergibt und dass wir 1 kriegen, wenn wir die Basis in den Logarithmus eingeben.

Logarithmus als Umkehrfunktion

Wir wissen, dass der Logarithmus eigentlich zu einer Potenz gehört:

\[ \log_a(x) = b \quad \Leftrightarrow \quad a^b = x \]

Wenn wir die Potenz auf der rechten Seite als unsere Funktion \(f\) betrachten, dann weist sie dem Argument \(b\) den Funktionswert \(x\) zu. Sie nimmt ein \(b\) und macht daraus eine Potenz, deren Wert \(x\) entspricht:

\[ f: \; b \mapsto x, \quad f(b) = a^b = x \]

Der Logarithmus macht genau das Umgekehrte: Er nimmt das \(x\) und macht daraus das passende \(b\):

\[ f^{-1}: \, x \mapsto b, \quad f^{-1} = \log_a(x) = b \]

Deshalb ist der Logarithmus mit Basis \(a\) die Umkehrfunktion der Exponentialfunktion mit Basis \(a\).

Allgemein gilt, dass wenn wir eine Funktion und ihre Umkehrung gleich nacheinander ausführen, erhalten wir wieder das ursprüngliche Argument:

\[ f(b) = f\Big( f^{-1}(x)\Big) = x \]

\[ f^{-1}(x) = f^{-1}\Big( f(b)\Big) = b \]

Der Logarithmus ist die Umkehrfunktion der Exponentialfunktion mit der gleichen Basis:

\[ a^{\big( \log_a(x)\big)} = x \]

\[ \log_a\big( a^b \big) = b \]

Analog gilt es auch für den natürlichen Logarithmus…

\[ e^{\big( \ln(x)\big)} = x \]

\[ \ln\big( e^b \big) = b \]

…und für den Zehnerlogarithmus:

\[ 10^{\big( \lg(x)\big)} = x \]

\[ \lg\big( 10^b \big) = b \]

Gleichungen mit Logarithmus lösen

Wenn wir eine Exponentialgleichung haben und die Unbekannte im Exponenten ist, können wir sie sehr einfach mit dem “Gegenmittel Logarithmus” 💊 lösen, wie wir im nachfolgenden Beispiel zeigen.

Graph des Logarithmus

Da der Logarithmus die Umkehrfunktion der Exponentialfunktion (mit der gleichen Basis) ist, erhalten wir den Graphen des Logarithmus mit einer Spiegelung an der 45°-Geraden \((y=x)\).

Wir wählen die natürliche Basis \(e\) :

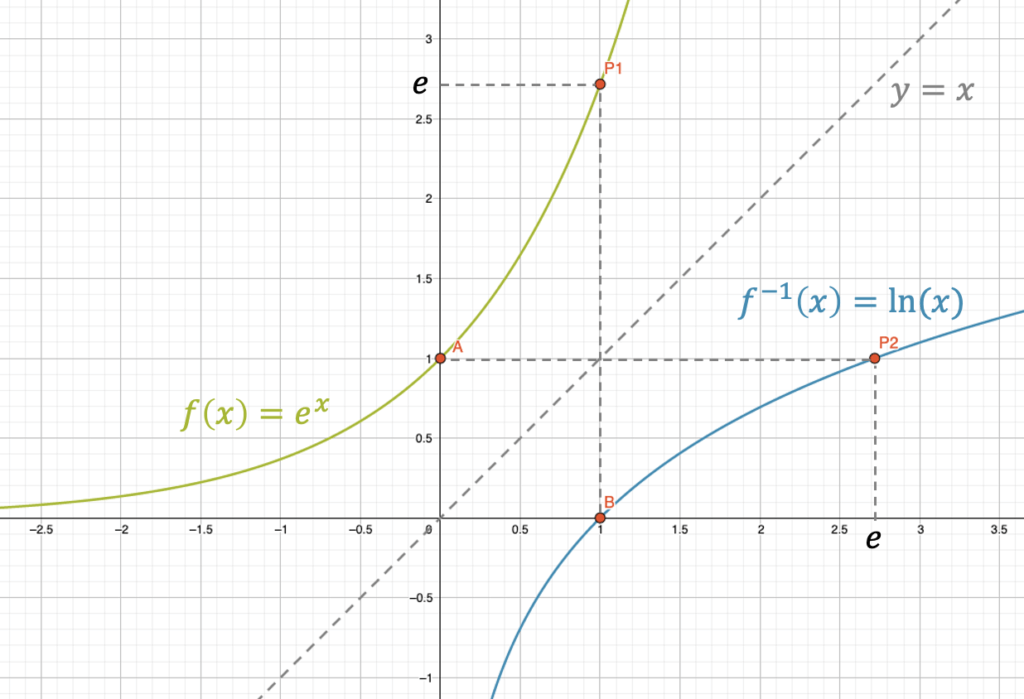
Wir sehen, dass der Logarithmus nur auf der rechten Hälfte vorkommt, d.h. nur für \(x>0\).

Für \(x\)-Werte, die nahe zu null liegen, fällt der Logarithmus fast senkrecht runter ins Negative. Das ist eine Asymptote, die wir wie folgt ausdrücken können:

\[ \lim_{x \rightarrow 0}\Big( \log(x) \Big) \rightarrow -\infty\]

Nach rechts steigt der Logarithmus und flacht immer mehr ab. Es wichtig zu wissen, dass er nie komplett abflacht, d.h. er steigt immer weiter, wenn auch immer weniger schnell.

Der Logarithmus ist, je weiter rechts wir gehen, die langsamste, steigende Funktion überhaupt!

Weil der Logarithmus aber trotz allem immer noch weiter steigt, gibt es keinen Grenzwert, den er anstrebt, sondern er steigt ins Unendliche:

\[ \lim_{x \rightarrow \infty}\Big( \log(x) \Big) \rightarrow +\infty\]

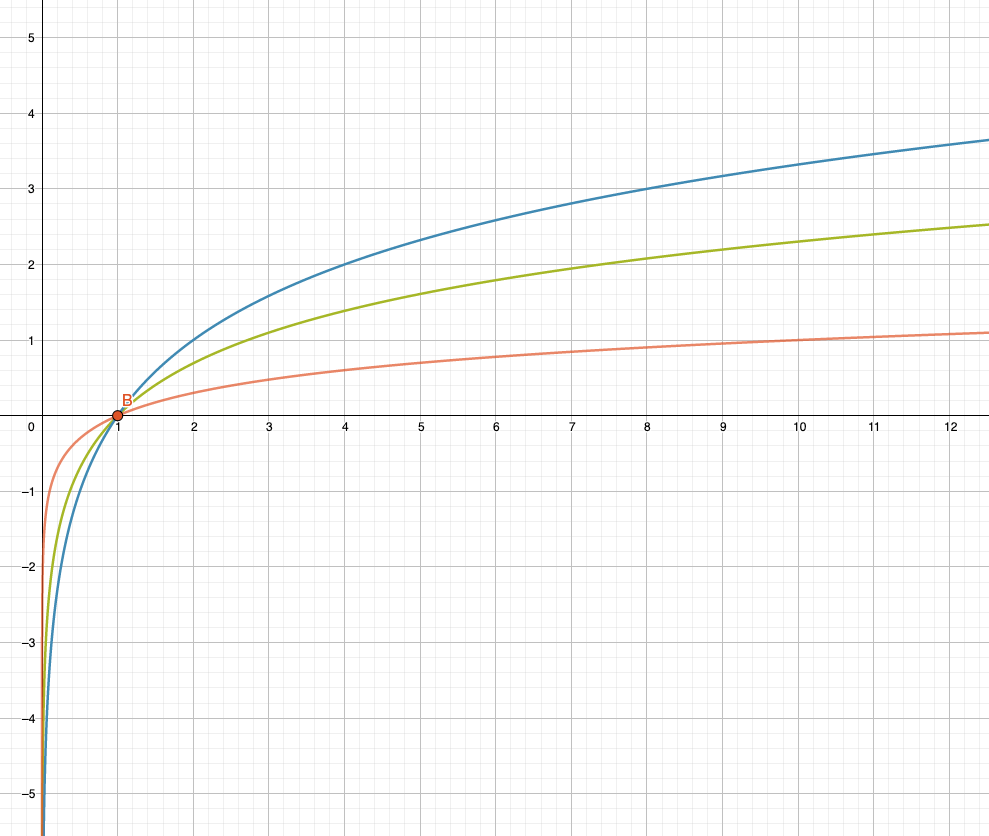
Logarithmen für Basen a<1

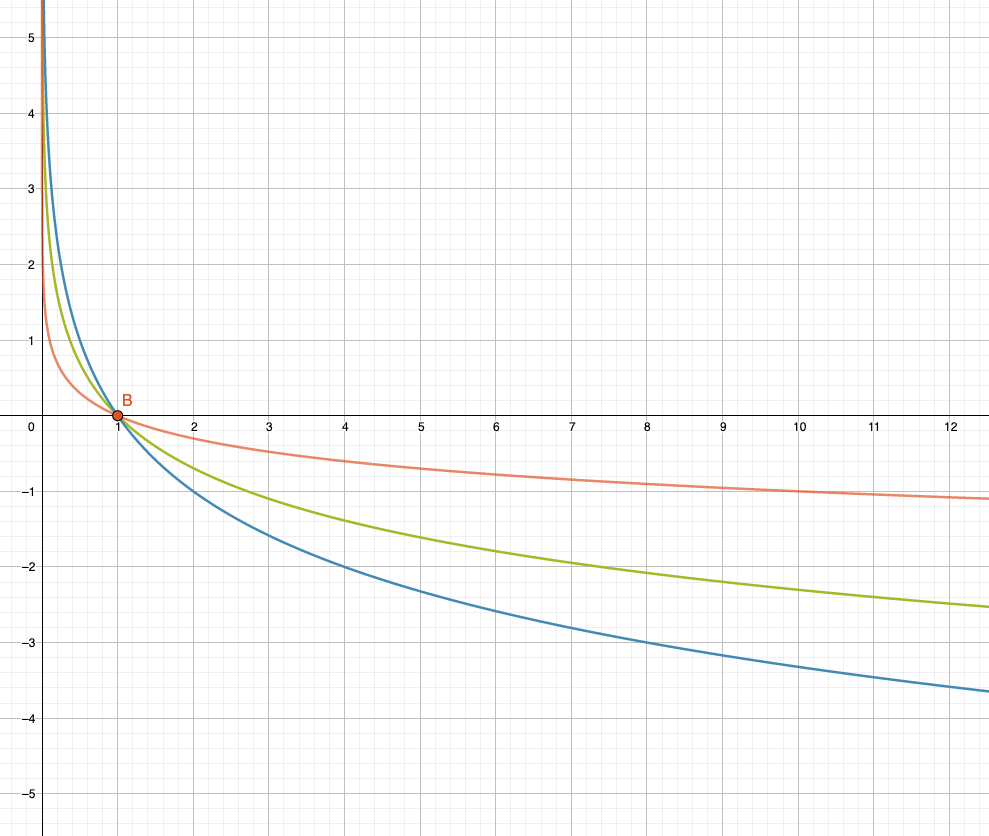
Für die Basis haben wir uns bis hierher auf \(a>1\) beschränkt, wie z.B. \(a=2\), \(a=e\) oder \(a=10\). Wie steht es mit sehr kleinen Basen aus, die zwar positiv (Bedingung!), aber kleiner als 1 sind? Wie wäre z.B. der Verlauf eines Logarithmus mit Basis \(a=\frac{1}{2}\) ?

Für diese Basis gilt beispielsweise:

\[ \log_{(1/2)}\Big( \frac{1}{2} \Big) = 1 \quad \Leftrightarrow \quad \Big( \frac{1}{2} \Big)^1 = \frac{1}{2} \]

\[ \log_{(1/2)} (2) = -1 \quad \Leftrightarrow \quad \Big( \frac{1}{2} \Big)^{-1} = \frac{1}{2^{-1}} = 2^1 = 2 \]

Ausserdem wird diese Kurve auch durch den Punkt B(1,0) gehen, der allen Logarithmen gemeinsam ist. Wir haben somit die folgenden drei Punkte, die diese Kurve ausmachen:

\[ (\frac{1}{2},1), \;\; B(1,0), \;\; (2,-1)\]

Es ist eine fallende Kurve, die von oben links oben nach unten rechts abfällt. In der folgenden Grafik ist es die blaue Kurve:

Ableitung Logarithmus

Die Ableitung der Logarithmusfunktion erhalten wir sehr einfach mit Hilfe der Ableitung einer Umkehrfunktion. Sie wird dort als Beispiel vorgerechnet. Der Logarithmus ist ja die Umkehrfunktion der Exponentialfunktion.