Exponentialfunktion

Exponentielles Wachstum

Das exponentiellen Wachstum ist besonders, weil es das grösste Wachstum überhaupt ist. Interessanterweise wächst es aber am Anfang viel schwächer als andere Funktionen.

Fast plötzlich “explodiert” es und lässt alle anderen Funktionen hinter sich.

In der nachfolgenden Tabelle vergleichen wir eine lineare, eine quadratische und eine exponentielle Funktion:

• Lineare Funktion: \(f(t) = 2t – 1\)
• Quadratische Funktion: \(f(t) = t^2\)
• Exponentialfunktion: \(f(t) = 0.5 \cdot 2^t\)

Punkt	A	B	C	D	E	F	G	H	I
Zeit t (in s)	1	2	3	4	5	6	7	8	9
Lineare Funktion	1	3	5	7	9	11	13	15	17
\(\Delta\)		+2	+2	+2	+2	+2	+2	+2	+2
Quadratische Funktion	1	4	9	16	25	36	49	64	81
\(\Delta\)		+3	+5	+7	+9	+11	+13	+15	+17
Exponentialfunktion	1	2	4	8	16	32	64	128	256
\(\Delta\)		+1	+2	+4	+8	+16	+32	+64	+128

Alle drei Funktionen starten bei 1 und wachsen unterschiedlich schnell an. Die Zeile \(\Delta\) zeigt uns, um wie viel der Funktionswert von Punkt zu Punkt zunimmt.

Bei der linearen Funktion kommt jedes Mal der gleiche Wert (+2) hinzu, wie bei einer Treppe. Es ist die Wachstumsrate bzw. die Steigung der Funktion. Bei der linearen Funktion ist die Steigung erwartungsgemäss konstant.

Die quadratische Funktion nimmt schneller zu. Wir sehen, dass die Steigung (Wachstumsrate \(\Delta\)) bei +3 startet und dann selber linear zunimmt. In der Differenzialrechnung werden wir sehen, dass das kein Zufall ist: Die Steigung einer quadratischen Funktion ist immer linear.

Die Exponentialfunktion, die wir hier anschauen, startet ebenfalls bei 1 und verdoppelt sich mit jedem Schritt. Hier fällt uns auf, dass die Zuwachsrate \(\Delta\) selber wie eine Exponentialfunktion ist.

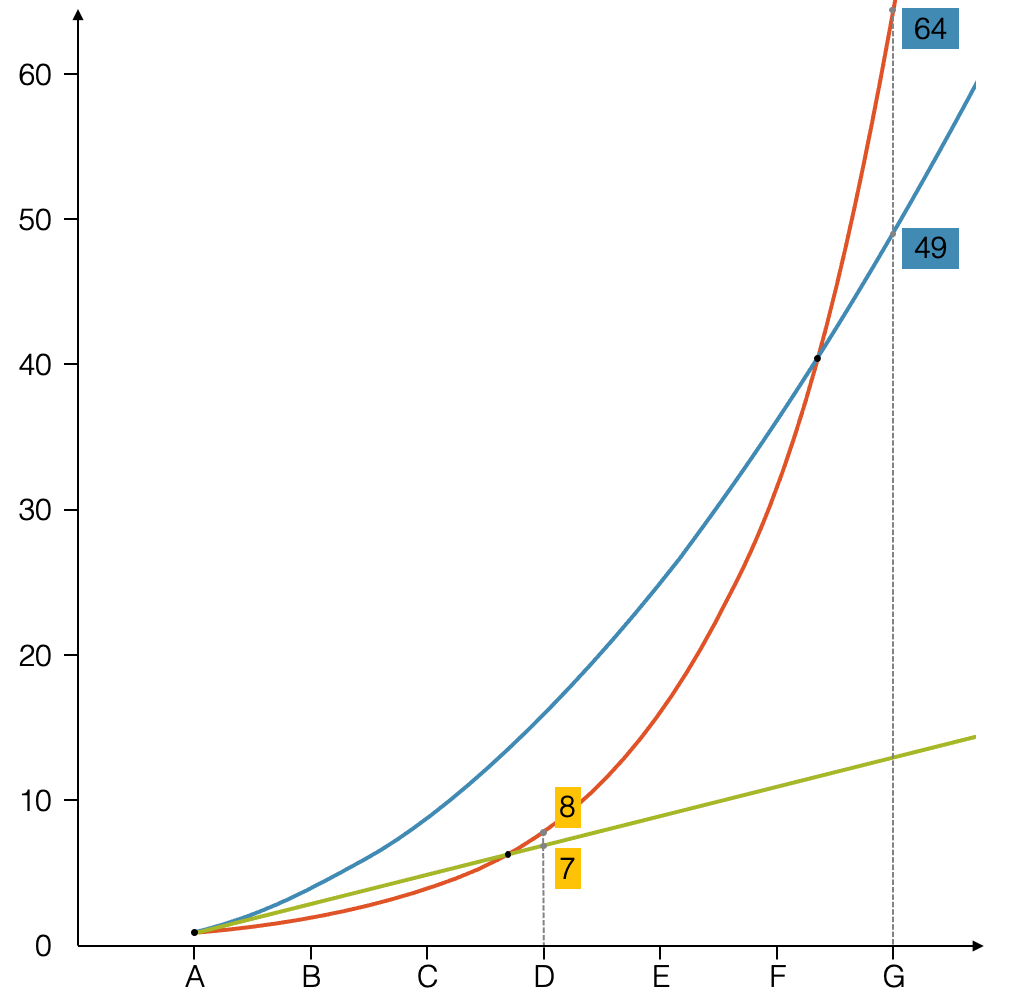
Im Vergleich der drei Funktionen erkennen wir, dass die lineare Funktion (grün) am langsamsten zunimmt und die Exponentialfunktion (rot) am stärksten. Interessanterweise ist aber die Exponentialfunktion ganz am Anfang die Langsamste!

Erst im Punkt D überholt die Exponentialfunktion (rot) die lineare Funktion (grün) und zwischen F und G auch die quadratische Funktion (blau).

Verdoppelungsfunktion

Schauen wir uns eine einfache Exponentialfunktion an mit Basis \(a=2\):

\[ f(x) = 2^x \]

Mit jeder Erhöhung von \(x\) um eins, verdoppelt sich der Funktionswert oder es kommt genau so viel dazu, wie es schon hat.

Beachte: Am Anfang ist der Unterschied nicht so klar zwischen einer Exponentialfunktion und einer Potenzfunktion, denn auch die Exponentialfunktion ist ja eine Potenz. Das Argument \(x\) bzw. \(t\) ist bei der Exponentialfunktion im Exponenten.

Vergleiche dazu eine Potenzfunktion (z.B. \(f(x)=x^3\)). Sie hat das Argument \(x\) in der Basis der Potenz.

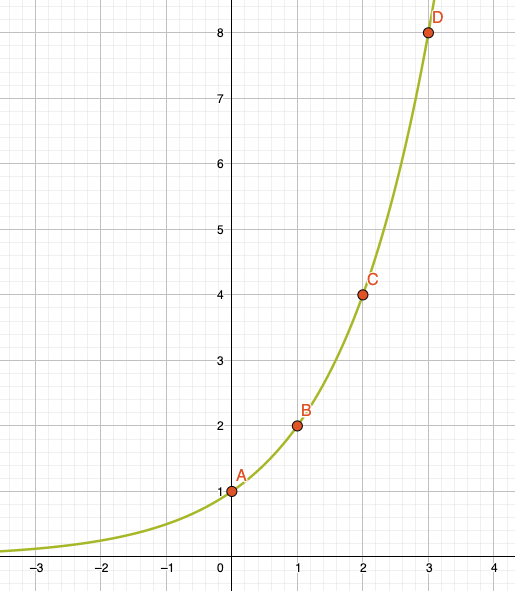
Der Punkt A ist ein gemeinsamer Punkt, denn er ist allen Exponentialfunktionen gemeinsam (abgesehen vom Vorfaktor):

\[ f(x) = a^x \quad \rightarrow \quad a^0 = 1 \quad (\forall a \in \mathbb{R}^+, \; a \neq 1 )\]

Egal welche Basis \(a\) wir haben, an der Stelle \(x=0\) erhalten wir immer den Funktionswert 1, d.h. alle Exponentialfunktionen mit allen möglichen Basen verlaufen durch den Punkt A(0,1).

Der Punkt bei \(x=1\) B(1,2) verrät uns die Basis 2, denn

\[ f(x) = a^x \quad \rightarrow \quad a^1 = a \]

Exponentielles Wachstum Beispiele

Wenn eine Funktion gerade so stark anwächst, wie sie ist (wenn die Steigung gleich ist, wie die Funktion selber), dann haben wir exponentielles Wachstum.

Aufgrund dieser Eigenschaft finden wir viele Beispiele, wo sich exponentielles Wachstum einstellt:

• Biologie: Die Anzahl neuer Zellen/Bakterien hängt ab von der Anzahl bestehender Zellen/Bakterien, die die Neuen produzieren.
• Finanzmathematik: Die Zinserträge sind abhängig von der Höhe des Kapitals, das diese abwirft.
• Physik: Die Anzahl freier Neutronen, die Urankerne spalten können, ist abhängig von der Anzahl Urankerne, die gespalten worden sind. (Kettenreaktion)

Exponentieller Zerfall

Etwas weniger bekannt ist der exponentielle Zerfall, der aber auch oft vokommt, z.B. in der Physik: radioaktiver Zerfall, Abkühlung, Entladung Kondensator.

Ist die Basis \(a < 1\) (z.B. \(a=\frac{1}{2}\)), dann wird bei jedem Einerschritt der aktuelle Funktionswert mit \(\frac{1}{2}\) multipliziert bzw. halbiert.

Dabei wird der Funktionswert immer kleiner, bleibt aber positiv: Wir haben dann den Fall des exponentiellen Zerfalls. Der Verlauf der Funktion geht wieder durch den gemeinsamen Punkt A und wir erkennen die Basis anhand des Funktionswerts im Punkt B.

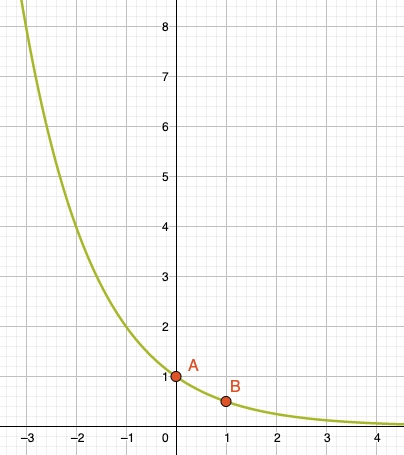
Für immer grösser werdende \(x\) wird ja der Funktionswert zunehmend kleiner, bleibt aber positiv. Er nähert sich dem Wert null an, obwohl er diesen nie erreicht. Man kann höchstens sagen, dass für \(x \rightarrow \infty\) gilt \(f(x) \rightarrow 0\) oder mit dem Grenzwert:

\[ \lim_{x \rightarrow \infty} f(x) = 0 \] 

Man nennt das auch asymptotische Annäherung der Funktion an die x-Achse, die in diesem Fall die Asymptote ist.

Der exponentielle Zerfall ist einfach das exponentielle Wachstum im “Rückwärtsgang”. Der Verlauf der Funktion wurde an der \(y\)-Achse gespiegelt.

\[ 2^x \quad \rightarrow \quad 2^{(-x)} = 2^{(-1) \cdot x} = \Big( 2^{-1} \Big)^x = \Big( \frac{1}{2} \Big)^x \]

Wenn der exponentielle Zerfall nicht zu null abklingt, sondern zu einem anderen Wert hin, dann spricht man von einer exponentiellen Abklingfunktion, z.B. der zeitliche Temperaturverlauf eines sich abkühlenden Gegenstands.

In der Wissenschaft und Technik haben wir oft auch eine Funktion, die sich von unten an einen höheren Wert anschmiegt. Eine solche Funktion nennen wir eine exponentielle Sättigungsfunktion oder ein beschränktes Wachstum (Sättigungskurve), z.B. beim Ansteigen einer Konzentration eines Stoffs in der Umgebung.

Ableitung Exponentialfunktion

Lösung der einfachsten Differentialgleichung

Eine Differentialgleichung ist eine Gleichung mit Ableitungsfunktionen. Die einfachste Differentialgleichung ist die Gleichheit von Funktion und ihrer ersten Ableitungsfunktion:

\[ f'(x) = f(x) \]

Was ist die Lösung dieser Differentialgleichung? Es ist die Funktion \(f(x)\), die diese Gleichung erfüllt.

Die einzige Funktion, die eine solche Gleichung erfüllen kann, ist eben die Exponentialfunktion \(f(x)=e^x\), denn:

\[ f'(x) = \frac{d}{dx}\Big(e^x\Big) = e^x = f(x) \]

Die einfachste Differentialgleichung kommt in der Natur oft vor: Die Zuwachsrate von Lebewesen ist proportional zu der bereits anwesenden Anzahl Lebewesen. Je mehr Eltern, desto mehr Junge gibt es. Resultat: Exponentielles Wachstum. Das gilt eigentlich für alle Lebewesen, inkl. dem Menschen. Wir schauen uns aber den etwas anschaulicheren Fall der Bakterienpopulation an.