Das Wichtigste in Kürze
Unter einer Hyperbel verstehen wir spezielle Kurven, deren zwei Scheitelpunkte sich gegenüberstehen, wie z.B. beim Verlauf von \(y=\frac{1}{x}\), oder allgemeiner mit einem ganzzahligen, positiven Exponenten \(n\):
\[ f(x) = \frac{1}{x^n} = x^{-n} \]
Für den Exponenten \(n\) gilt: \(n \in \mathbb{N}\), womit auch gegeben ist, dass \(n>0\)
Als Hyperbelfunktionen verstehen wir, analog zu den trigonometrischen Funktionen, die Funktionen, die zur Einheitshyperbel \(x^2 – y^2 = 1\) gehören.
Ihnen wird ein “h” für den Zusatz hyperbolicus angehängt:
-
- Sinus hyperbolicus: \(\sinh(x)\)
-
- Kosinus hyperbolicus: \(\cosh(x)\)
-
- Tangens hyperbolicus: \(\tanh(x)\)
Es gelten die folgenden praktischen Identitäten:
\[ \sinh(x) = \frac{1}{2}\big(e^x-e^{-x}\big) \]
\[ \cosh(x) = \frac{1}{2}\big(e^x+e^{-x}\big) \]
\[ \tanh(x) = \frac{\sinh(x)}{\cosh(x)} \]
Erste Ableitungsfunktionen der Hyperbelfunktionen:
\[ \frac{d}{dx}\big( \sinh(x) \big) \quad = \quad \cosh(x) \]
\[ \frac{d}{dx}\big( \cosh(x) \big) \quad = \quad \sinh(x) \]
\[ \frac{d}{dx}\big( \tanh(x) \big) \quad = \quad \frac{1}{\cosh^2(x)} \quad \]
\[ = \quad 1-\tanh^2(x) \]
\[ \frac{d}{dx}\big( \coth(x) \big) \quad = \quad -\frac{1}{\sinh^2(x)} \quad \]
\[ = \quad 1-\coth^2(x) \]
Hyperbeln mit ungeraden Exponenten
Für ungerade Exponenten \(n\) kriegen wir Verläufe, die zwar unterschiedlich aussehen, sonst aber viel gemeinsam haben.
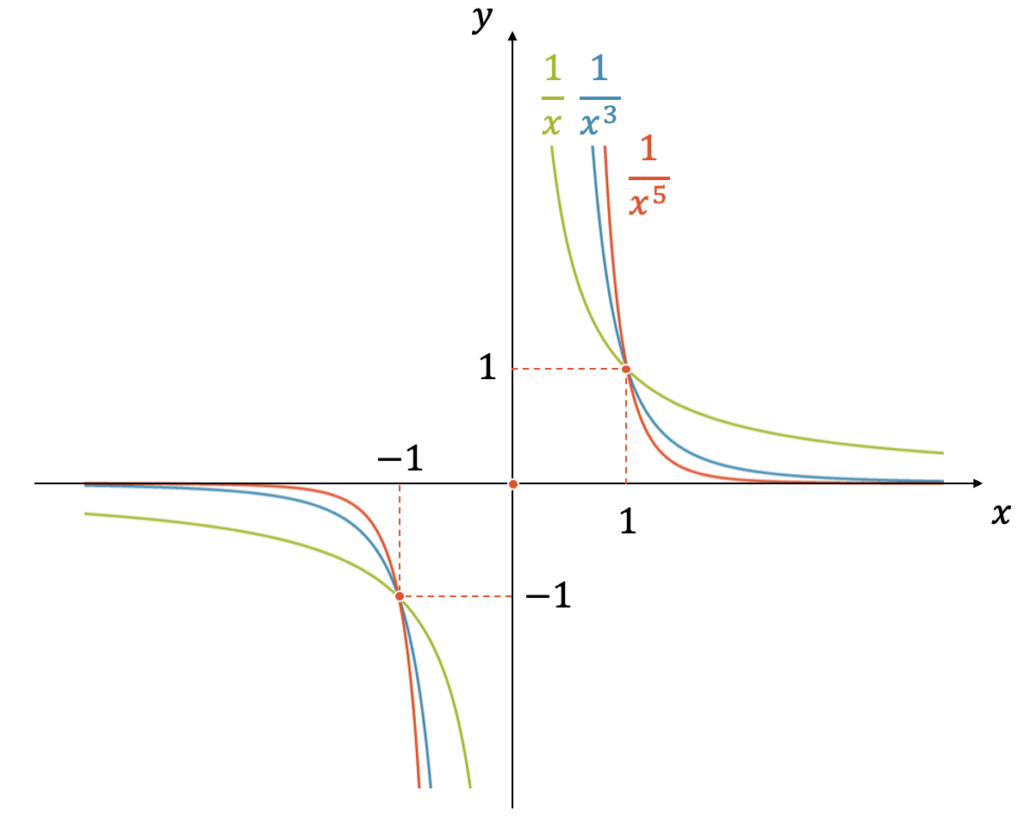
Nachfolgend sind ihre Eigenschaften aufgelistet:
- Die Funktionen verlaufen ausschliesslich im Quadranten unten links und im Quadranten oben rechts
- Ihre gemeinsamen Punkte sind: \((-1,-1)\) und \((1,1)\), unabhängig von \(n\). In diesen Punkten wechseln die Verläufe von steil zu flach bzw. umgekehrt
- Dort wo die Verläufe steil sind, sind die Funktionen mit grösserem \(n\) steiler als solche mit kleinerem \(n\)
- Dort wo die Verläufe flach sind, haben die Funktionen mit grösserem \(n\) einen kleineren Funktionswert als diejenige mit kleinerem \(n\)
- Für \(x\)-Werte nahe dem Ursprung, d.h. mit sehr kleinem absoluten Betrag, “explodieren” die Verläufe ins Positive bzw. Negative. Die Stelle \(x=0\) ist eine Unstetigkeitsstelle.
Beispiel: Unbekannter Exponent
Die Funktion \(f\) hat als Verlauf eine Hyperbel. Finde den Exponenten \(n\), wenn die Funktion durch den Punkt \(P\) verläuft.
\[ P(3,\frac{1}{243}) \]
Hyperbeln mit geraden Exponenten
Vieles ist bei den Hyperbeln mit geraden Exponenten \(n\) gleich, wie bei den Hyperbeln mit ungeraden Exponenten. Der augenfälligste Unterschied ist jedoch, dass wir ausschliesslich positive Funktionswerte haben.
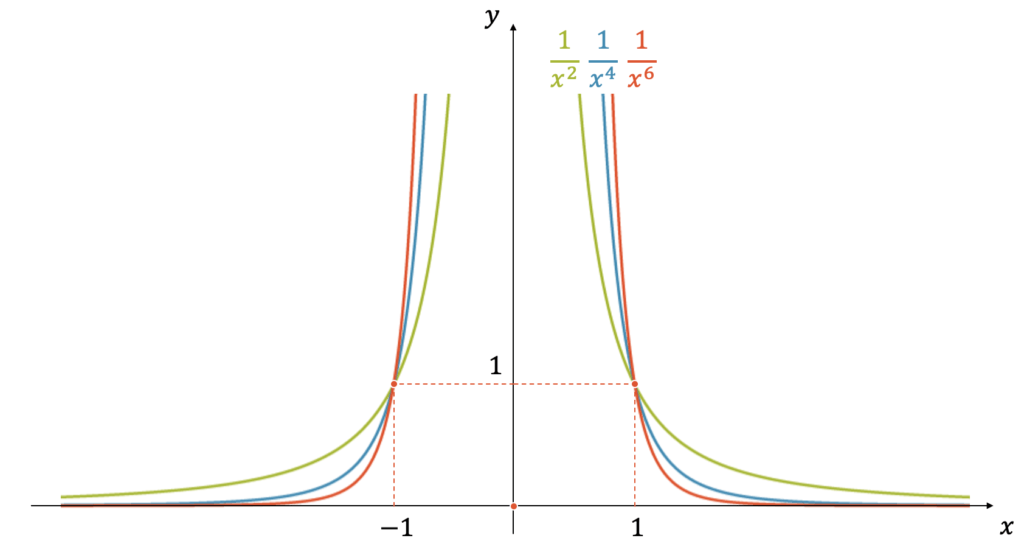
Nachfolgend sind ihre Eigenschaften aufgelistet:
- Die Funktionen verlaufen nur in den beiden oberen Quadranten, d.h. die Funktionswerte sind immer positiv
- Ihre gemeinsamen Punkte sind: \((-1,1)\) und \((1,1)\), unabhängig von \(n\)
- Je grösser \(n\), desto steiler verlaufen die Funktionen im steilen Bereich und desto kleiner sind die Funktionswerte im flachen Bereich
- Der Ursprung ist eine Unstetigkeitsstelle und die Funktionswerte “explodieren” zu unendlich grossen Werten
“Hyperbelfunktionen sind wie die trigonometrischen Funktionen, jedoch für die Welt der Kegelschnitte und Ellipsen”
Hyperbelfunktionen
Im Einheitskreis hatten wir die trigonometrischen Funktionen hergeleitet. Die Gleichung des Einheitskreises war (Gleichung eines Kreises mit Radius 1):
\[ x^2 + y^2 = 1 \]
Nun gibt es analog die Einheitshyperbel mit dem einzigen Unterschied, dass es sich um eine Differenz statt Summe handelt:
\[ x^2 – y^2 = 1 \]
Wenn wir die gleichen Überlegungen, wie damals bei den trigonometrischen Funktionen machen, erhalten wir die Hyperbelfunktionen:
Ihnen wird ein “h” für den Zusatz hyperbolicus angehängt:
- Sinus hyperbolicus: \(\sinh(x)\)
- Kosinus hyperbolicus: \(\cosh(x)\)
- Tangens hyperbolicus: \(\tanh(x)\)
Sie verhalten sich sehr ähnlich zu den trigonometrischen Funktionen \(\sin(x)\), \(\cos(x)\) und \(\tan(x)\). Meistens sind es nur unterschiedliche Vorzeichen.
Ableitung Hyperbelfunktionen
Dieser Artikel befasst sich im Speziellen mit der Ableitung der Hyperbelfunktionen. Für Aufgabensammlungen, Lernziele, Mini-Tests zu Ableitungen schaust du am besten im Hauptartikel zu den Ableitungsfunktionen nach.
Die Hyperbelfunktionen \(\sinh(x)\), \(\cosh(x)\) und \(\tanh(x)\) verhalten sich auch bei der Ableitung sehr ähnlich zu den trigonometrischen Funktionen. Es gibt Unterschiede bei den Vorzeichen.
Beispiel: Zweite Ableitung von sinh(x)
Zeige, dass \(\frac{d^2}{dx^2}\sinh(x) = \sinh(x)\), unter Benützung der Identitäten:
\[ \sinh(x) = \frac{1}{2}\big(e^x-e^{-x}\big) \]
\[ \cosh(x) = \frac{1}{2}\big(e^x+e^{-x}\big) \]
Lernziele
- Du kennst den Verlauf von Hyperbeln und vor allem den Unterschied zwischen den Hyperbeln mit ungeradem Exponenten und den Hyperbeln mit geradem Exponent.
- Du weisst, dass die Hyperbeln den gemeinsamen Punkt (1,1) haben. Je nach Exponent, ist der andere gemeinsame Punkt über oder unter der \(y\)-Achse: (-1, +1) bzw. (-1,-1)
- Du weisst, dass es die Hyperbelfunktionen gibt und dass sie sich sehr ähnlich zu den trigonometrischen Funktionen verhalten.
- Du kennst die Identitäten der Hyperbelfunktionen, die es erlaubt, sie als Summe bzw. Differenz von Exponentialfunktionen zu schreiben
Weitere Links
Hyperbelfunktion (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.