Integrale gerader und ungerader Funktionen

In der Integralrechnung ist es manchmal sehr nützlich, wenn die zu integrierenden Funktionen gerade oder ungerade Funktionen sind, denn dann können wir spezielle Eigenschaften nutzen, um das Integral einfacher zu berechnen.

Eine gerade Funktion \(f(x)\) ist spiegelsymmetrisch zur \(y\)-Achse, d.h. der Funktionswert an einer Stelle \(x\) ist gleich an der “gespiegelten Stelle” \((-x)\). Wir können deshalb für eine solche Funktion schreiben:

\[ f(x) = f(-x) \]

Beispiele für gerade Funktionen sind z.B. \(\cos(x)\) oder \(|x|\).

Eine ungerade Funktion \(g(x)\) ist punktsymmetrisch zum Ursprung \((0,0)\), d.h. der Funktionswert an der Stelle \(x\) ist in gleichem Abstand von der \(y\)-Achse gleich, aber mit umgekehrtem Vorzeichen, also zusätzlich zur \(x\)-Achse gespiegelt. Mathematisch lässt sich schreiben:

\[ g(x) = -g(-x) \]

Beispiele für ungerade Funktionen sind z.B. \(\sin(x)\) oder die 45°-Gerade \(g(x)=x\).

Beispiel

Berechne das folgende Integral:

\[ \int_{-3\pi/4}^{+3\pi/4} \sin(x) \; dx \]

---

Die Sinus-Funktion ist eine ungerade Funktion, denn es gilt:

\[ \sin(x) = – \sin(-x) \]

Die Fläche links der \(y\)-Achse hat ein negatives Vorzeichen, diejenige rechts der \(y\)-Achse ist positiv. Da die Funktion punktsymmetrisch ist, sind beide Flächen vom Betrag her gleich.

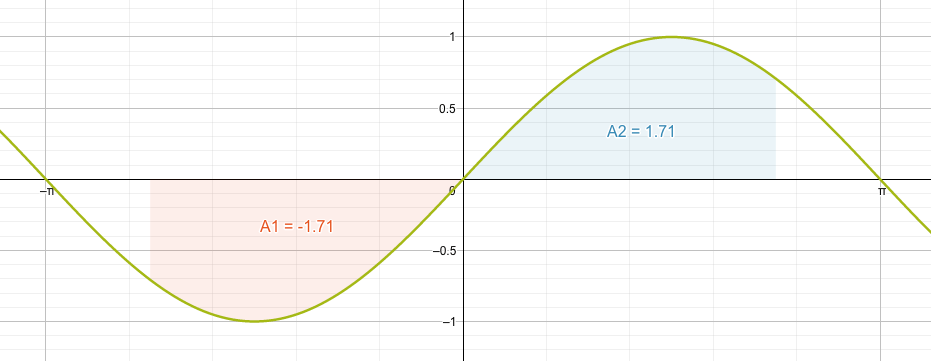
Wenn beide Flächen gleich gross sind, aber umgekehrtes Vorzeichen haben, so hebt sich die Summe genau auf. Das Integral hat den Wert null:

\[ \int_{-3\pi/4}^{+3\pi/4} \sin(x) \; dx = 0 \]

Wir können das Resultat auch rechnerisch überprüfen:

\[ \int_{-3\pi/4}^{+3\pi/4} \sin(x) \; dx = \Big[ -\cos(x) \Big]_{-3\pi/4}^{+3\pi/4} \]

\[ = \big(-\cos(3\pi/4)\big) – \big(-\cos(-3\pi/4)\big) \]

\[ = -\cos(3\pi/4) + \cos(-3\pi/4) \]

\[ = -\big(-\frac{1}{\sqrt{2}}\big) + \big(-\frac{1}{\sqrt{2}}\big) \]

\[ = \frac{1}{\sqrt{2}} – \frac{1}{\sqrt{2}} = \underline{\;0\;} \]

Beachte, dass der Kosinus eine gerade Funktion ist, d.h.

\[ \cos(3\pi/4) = \cos(-3\pi/4) = -\frac{1}{\sqrt{2}} \]

Beispiel

Berechne das folgende Integral

\[ \int_{-1}^{+1} e^{-|x|} \; dx \]

---

Bei Funktionen mit Beträgen müssen wir immer eine Fallbetrachtung machen. Für die positiven \(x\)-Werte braucht es die Betragsstriche nicht, d.h. es gilt:

\[ x > 0 \qquad e^{-|x|} = e^{-x} \]

Für negative \(x\)-Werte machen die Betragsstriche aus der negativen Zahl eine positive Zahl. Das Vorzeichen wird geändert. Wenn \(x\) negativ ist, dann ist \((-x)\) positiv. Wir können deshalb so schreiben:

\[ x < 0 \qquad e^{-|x|} = e^{-(-x)} = e^x \]

Das Integral teilen wir in zwei Integrale auf, eines für die negativen \(x\)-Werte und eines für die positiven \(x\)-Werte:

\[ \int_{-1}^{+1} e^{-|x|} \; dx \;\; = \;\; \int_{-1}^{0} e^{x} \; dx + \int_{0}^{+1} e^{-x} \; dx \]

Jetzt können wir die beiden Integrale lösen. Das erste Integral ergibt:

\[ \int_{-1}^{0} e^x \; dx = \big[ e^x \big]_{-1}^{0} \]

\[ = e^0 – e^{-1} = 1 – e^{-1} \]

Das zweite Integral ergibt die gleiche Fläche:

\[ \int_{0}^{+1} e^{-x} \; dx = \big[ -e^{-x} \big]_{0}^{+1} \]

\[ = -e^{-1} – (-e^0) = 1 – e^{-1} \]

Damit ist die Summe der beiden Integrale:

\[ \int_{-1}^{+1} e^{-|x|} \; dx = \underline{2 \cdot \big(1 – e^{-1}\big)} \]

Dass die beiden Integrale gleich gross waren, sollte nicht erstaunen, denn \(e^{-|x|}\) ist eine gerade Funktion und somit spiegelsymmetrisch bezüglich der \(y\)-Achse. Die beiden Teilintegrale sind wegen dieser Symmetrie gleich gross. Ausserdem haben sie das gleiche Vorzeichen. Mit dieser Erkenntnis hätten wir auf die Berechnung des zweiten Integrals verzichten können.