Funktionen können sehr komplex sein und in gewissen Fällen bringen sie sogar Computer ins Schwitzen. Die Mathematik hat mit Hilfe der Differentialrechnung ein unglaublich starkes Werkzeug hierzu: Die Linearisierung. Es ist eigentlich ganz einfach. Die Funktion, die meistens einen geschwungenen, gekrümmten Verlauf hat, wird an einer bestimmen Stelle durch eine lineare Funktion ersetzt. Es handelt sich dabei um die Stelle, die uns am meisten interessiert und für welche wir Berechnungen anstellen müssen. Der Vorteil einer linearen Funktion ist ihre Einfachheit!
Betrachten wir eine Funktion \(u(x)\) und legen eine lineare Funktion an der Stelle \(x\) an die Funktion heran, so dass sie eine Tangente \(t(x)\) bildet. Solange wir uns nicht zu weit von der Stelle \(x\) entfernen, ist die Tangente eine akzeptable Näherung der sonst gekrümmten Funktion \(u(x)\):
\[ t(x) \;\; \approx \;\; u(x) \]
Wie kommen wir zu dieser linearen Funktion? Dazu betrachten wir den Verlauf der Funktion \(u(x)\).
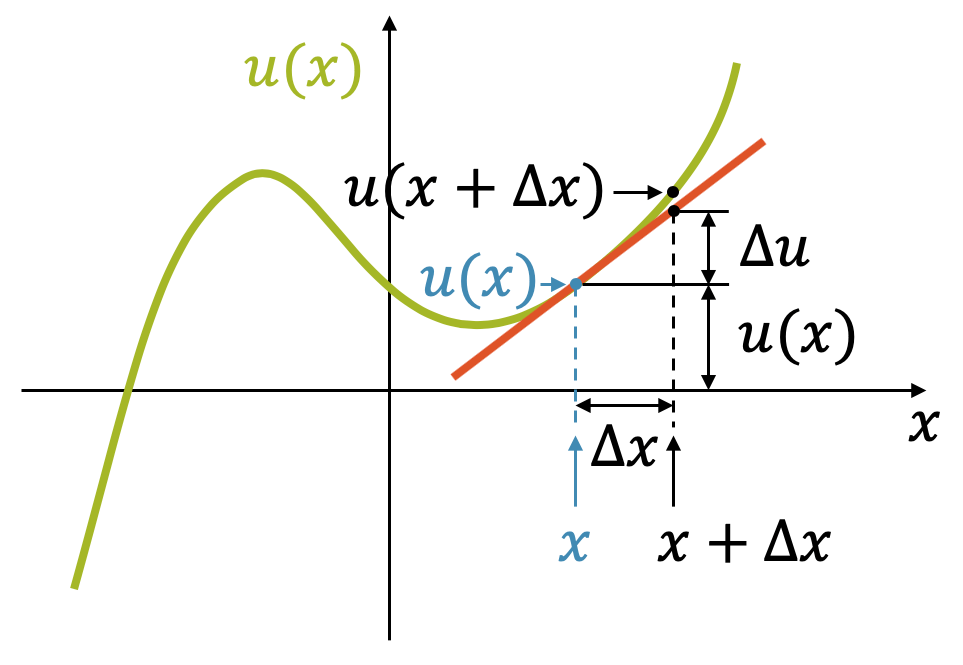
Die Abweichung der Tangente von \(u(x)\) erkennen wir, sobald \(\Delta x\) genug gross ist.
Die lineare Funktion \(t(x)\) hat die übliche Form mit der Steigung \(m\) und dem Achsabschnitt \(q\) (Ort, an welchem die Gerade die \(y\)-Achse schneidet):
\[ t(x) = m \cdot x + q \]
Nun wissen wir, dass die Steigung von \(u(x)\) in \(x\) gleich der ersten Ableitung in \(x\) ist:
\[ m = u'(x) \]
Desweiteren geht die lineare Funktion an der Stelle \(x\) durch den gleichen Punkt, wie die Funktion \(u(x)\). Sie berühren sich dort. So können wir den Achsabschnitt \(q\) bestimmen:
\[ t(x) = m \cdot x + q \stackrel{!}{=} u(x) \]
\[ \rightarrow q = u(x) – m \cdot x \]
\[ \rightarrow q = u(x) – u'(x) \cdot x \]
Die Tangente \(t(x)\) berührt die (nicht-lineare) Funktion \(u(x)\) an der Stelle \(x\). Für kleine Abweichungen von dieser Stelle, können die Funktionswerte von \(t(x)\) als einfacher zu berechnende Näherung für \(u(x)\) benutzt werden.
\[ t(x) = m \cdot x + q \quad \approx \quad u(x) \]
Die Steigung \(m\) und den Achsabschnitt \(q\) berechnen wir wie folgt:
\[ m = u'(x) \]
\[ q = u(x) – u'(x) \cdot x \]
Beispiel
Lege an die Funktion \(f(x)=x^2-6x+5\) eine Tangente an der Stelle \(x=5\) und bestimme ihre Funktionsgleichung. Untersuche dann den Funktionswert \(f(5.1)\) und vergleiche ihn mit dem Wert, den die Tangente in \(x=5.1\) liefert.
Für die Steigung der Tangente \(t(x)\) brauchen wir die erste Ableitung von \(f(x)\) in \(x=5\). Wir benutzen die Regel für die Ableitung einer Potenzfunktion und setzen \(x=5\) ein:
\[ f'(x) = 2x-6 = 2 \cdot 5 – 6 \]
\[ = 10 – 6 = 4 \]
Jetzt berechnen wir \(f(x)\) für \(x=5\):
\[ f(x=5) = 5^2 – 6 \cdot 5 + 5 \]
\[ = 25 – 30 + 5 = 0 \]
Damit können wir den Achsabschnitt bestimmen:
\[ q = f(x) – f'(x) \cdot x \]
\[ = 0 – 4 \cdot 5 = -20 \]
Die Tangentenfunktion lautet also:
\[ t(x) = \underline{4x – 20} \]
Für die Stelle \(x=5.1\) erhalten wir
\[ f(x=5.1) = 5.1^2 – 6 \cdot 5.1 + 5 \]
\[ = 26.01 – 30.6 + 5 = 0.41 \]
\[ t(x=5.1) = 4 \cdot 5.1 – 20 \]
\[ = 20.4 – 20 = 0.40 \]
Der Funktionswert von \(t(x)\) weicht um \(0.01\) von \(f(x)\) ab, was einem relativen Fehler von 2.5% entspricht. Wir erkennen bereits an diesem einfachen Beispiel, dass die Berechnung von \(t(5.1)\) einfacher ist als die Berechnung von \(f(5.1)\).
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.