Flächenberechnung

Mit dem unbestimmten Integral ermitteln wir die Stammfunktion. Mit dem bestimmten Integral berechnen wir die Fläche zwischen den Funktionswerten und der \(x\)-Achse.

Wie Flächen aus bestimmten Integralen berechnet werden, schauen wir uns an einem Beispiel an. Gesucht ist die Fläche \(A\) aus dem folgenden Integral:

\[ A = \int_{-3}^{2} x^2+2x-3\,dx \]

Die Funktion \(f(x)=x^2+2x-3\) integrieren wir zuerst in einem unbestimmten Integral, um die Stammfunktion \(F(x)\) zu erhalten. Wir finden:

\[ \int \big( x^2+2x-3 \big) \,dx = \frac{1}{x^3}+x^2-3x+C \]

Jetzt kontrollieren wir unsere Stammfunktion mit dem Hauptsatz der Integralrechnung, d.h. wir schauen, ob die Ableitung der Stammfunktion wieder zu der ursprünglichen Funktion \(f(x)\) führt:

\[ \frac{d}{dx} \Big( \frac{1}{3}x^3+x^2-3x+C\Big) = x^2+2x-3 \]

Wir schreiben jetzt die Stammfunktion in zwei eckigen Klammern auf und fügen rechts davon die beiden Integrationsgrenzen hinzu. Diese Notation ist eine Kurzschreibweise für die Differenz zwischen \(F(+2)\) und \(F(-3)\):

\[ A = \Big [\, \frac{1}{3}x^3+x^2-3x+C \, \Big]_{-3}^{+2} = F(+2) – F(-3) \]

Wir setzen jetzt die Argumente \(-3\) und \(+2\) in die Stammfunktionen ein:

\[ A = \Big (\frac{1}{3}2^3+2^2-3\cdot2+C \Big) \]

\[ – \Big (\frac{1}{3}(-3)^3+(-3)^2-3\cdot(-3)+C \Big) \]

\[ \require{cancel} A = \Big (\frac{8}{3}+4-6+C \Big) – \Big ((\cancel{-9})+\cancel{9}+9+C \Big) \]

\[ \require{cancel} A = \frac{8}{3}+4-6+\cancel{C}-9-\cancel{C} = \frac{2}{3} – 9 = \underline{-8\frac{1}{3}} \]

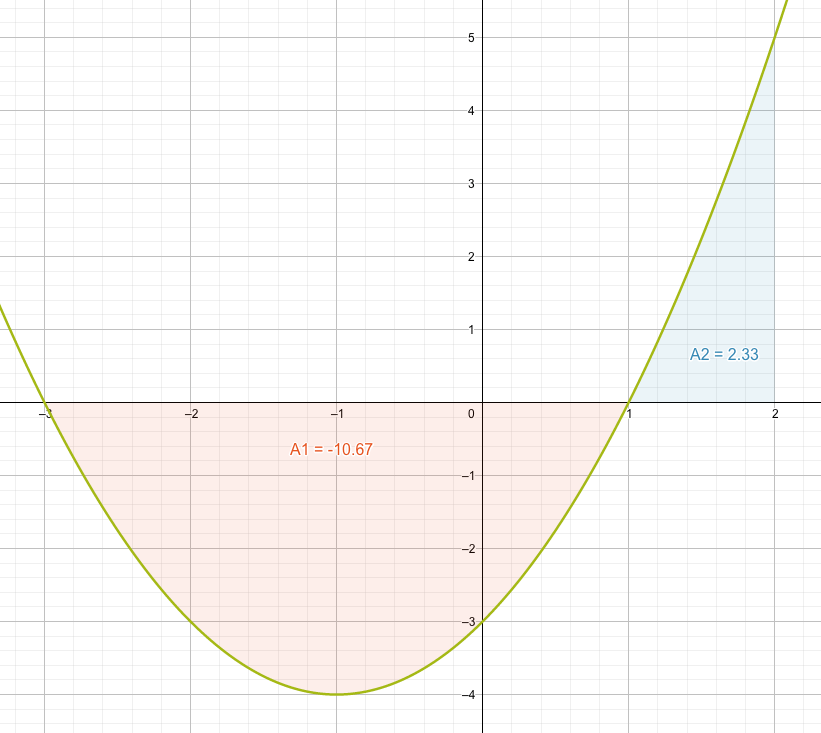
Das Resultat ist eine negative Fläche, denn der Anteil der Fläche unter der \(x\)-Achse überwiegt, wie wir in der nachfolgenden Grafik erkennen können:

Von \(x=-3\) bis \(x=1\) haben wir eine negative Fläche von total \(A_1=-10\frac{2}{3}\). Von der Stelle \(x=1\) bis \(x=2\) ist die Fläche positiv: \(A_2=+2\frac{1}{3}\). Die Summe der beiden Flächen ist dann:

\[ A = A_1 + A_2 = -10\frac{2}{3} + 2\frac{1}{3} \]

\[ A = -8\frac{1}{3} \]

Beachte, dass die unbekannte Konstante durch die Differenz herausgefallen ist. Das wird bei jedem bestimmten Integral so sein. Wir werden deshalb in Zukunft die Konstante \(C\) nicht mehr in die eckige Klammer schreiben müssen.

Die Fläche entspricht dem bestimmten Integral von \(a\) bis \(b\):

\[ \int_{a}^{b} f(x)\,dx = \big[ F(x) \big]_{a}^{b} = F(b) – F(a) \]

Beispiel

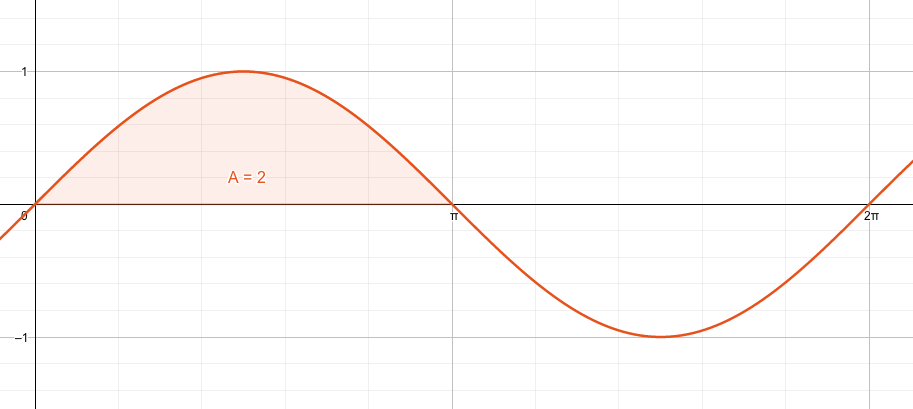
Berechne die Fläche unter der Sinuskurve von \(0\) bis \(\pi\).

---

Wir schreiben zuerst das unbestimmte Integral auf und finden die Stammfunktion (durch Erraten). Wir wissen ja, dass \(\frac{d}{dx}\big(\cos(x)\big) = -\sin(x)\). Somit ändern wir das Vorzeichen und erhalten so:

\[ \int \sin(x) dx = -\cos(x) + C \]

Jetzt schreiben wir das bestimmte Integral und lösen es mit der Stammfunktion \(F(x)=-\cos(x)\):

\[ \int_{0}^{2\pi} \sin(x) dx = \big[ -\cos(x) \big]_{0}^{2\pi} \]

\[ \big( -\cos(2\pi) \big) – \big( -\cos(0) \big) = \big(-(-1)\big) – \big(-1\big) = 1+1 = \underline{2}  \]