Die ganze Differenzialrechnung befasst sich mit der Frage: “Wie kann ich die Steigung einer Funktion bestimmen?”. Wir werden sehen, dass diese Fragestellung eine unglaublich fundamentale Bedeutung, vor allem in den Ingenieur- und Naturwissenschaften, durchaus aber auch in der Wirtschaftswissenschaft und anderen Bereichen.
Wenn wir eine Funktion aufgestellt haben und die Steigung in jedem Punkt kennen, wissen wir auch, in welchen Punkten die Funktion keine Steigung hat, d.h. wo die Steigung null ist. Diese Punkte sind von besonderem Interesse, denn sie entsprechen Maxima oder Minima. Kennen wir die Steigung einer Funktion, können wir sagen, wo sie extreme Werte annimmt. Der Ökonom kann beispielsweise berechnen, für welche Produktionsmenge der Gewinn maximal sein wird. Der Ingenieur kann z.B. die schwächste Stelle im Flügel eines Flugzeugs finden und diese dann besonders anschauen. Der Biologe kann ein natürliches Gleichgewicht bestimmen etc.
Betrachten wir als Erstes das Beispiel einer Parabel. Uns interessiert die Steigung der Parabel \(y(x)=\frac{1}{4}x^2\) im Punkt A(2,1).
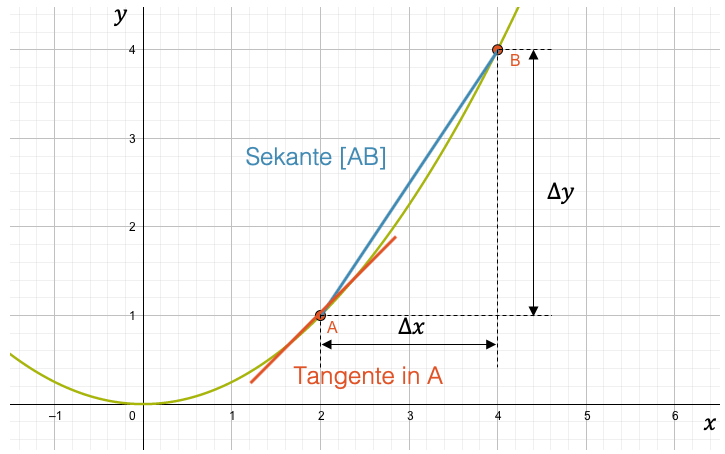
Die Tangente im Punkt A(2,1) hätte die von uns gesuchte Steigung. Wir können zwar eine Tangente ungefähr zeichnen, aber wie sollen wir ihre Steigung bestimmen?
Einfacher ist es die Steigung der Sekante zu bestimmen. Nehmen wir beispielsweise die Sekante, die die Punkte A(2,1) und B(4,4) verbindet, so erhalten wir \(\Delta x = 4-2 = 2\) und \(\Delta y = 4-1 = 3\). Die Steigung der Sekante ist durch den Differenzenquotienten gegeben:
\[ m_{Sekante} = \frac{\Delta y}{\Delta x} = \frac{3}{2} = 1.5 \]
Wir wissen zwar, dass dieses Resultat nicht ganz stimmt, denn Sekante und Tangente sind nicht das Gleiche. In der Grafik sehen wir, dass die Sekante steiler als die Tangente ist. Die wahre Lösung muss kleiner sein als 1.5.
Jetzt kommt der Trick: Der Unterschied zwischen der Sekante und der Tangente wird kleiner, je kleiner wir das Steigungsdreieck für die Sekante machen. Je näher wir den Punkt B zu A bringen, desto kleiner wird die Differenz. Für ein \(\Delta x\), das so klein ist, dass es gegen null geht, ist der Fehler ebenfalls klein und geht gegen null. Wir schreiben deshalb:
\[ m_{Tangente} = \lim_{\Delta x \rightarrow 0} \Big (\frac{\Delta y}{\Delta x} \Big ) \]
Weil wir ja nicht durch null teilen dürfen, dürfen wir auch nicht einfach \(\Delta x = 0\) setzen. Wir benutzen deshalb den Grenzwert für \(\Delta x \rightarrow 0\). Die von uns gesuchte Steigung entspricht deshalb dem Grenzwert des Differenzenquotienten, wenn wir \(\Delta x\) gegen null laufen lassen. Jetzt können wir unsere Steigung verallgemeinern. Wir setzen dazu:
\[ \Delta y = f(x_0 + \Delta x) – f(x_0) \]
Die Steigung der Sekante wird durch den Differenzenquotienten beschrieben:
\[ m_{\text{Sekante}} = \frac{\Delta y}{\Delta x} = \frac{f(x_0 + \Delta x) – f(x_0)}{\Delta x} \]
Die Steigung der Funktion \(f(x)\) im Punkt \(x=x_0\) entspricht der Steigung der Tangente in diesem Punkt. Sie kann mit dem Differenzialquotienten berechnet werden:
\[ y'(x_0) = \lim_{\Delta x \rightarrow 0} \Big (\frac{f(x_0 + \Delta x) – f(x_0)}{\Delta x} \Big ) \]
Jedem Ort \(x_0\) wird mit \(y'(x_0)\) eine Steigung zugeordnet. \(y'(x)\) ist deshalb selber wieder eine Funktion des Ortes und wird (erste) Ableitungsfunktion der Funktion \(y(x)\) genannt und mit einem Strich versehen. Weitere Schreibweisen für die erste Ableitung an der Stelle \(x_0\):
\[ y'(x_0) = f'(x_0) = \frac{d}{dx} y(x) \Bigg|_{x_0} = \frac{dy}{dx} \Bigg|_{x_0} \]
Wir können jetzt an unserem Beispiel die Steigung der Tangente im Punkt A(2,1) berechnen. Um den Differenzialquotienten zu berechnen, benötigen wir:
\[ f(x_0) = \frac{1}{4}x_0^2 \]
\[ f(x_0 + \Delta x) = \frac{1}{4}(x_0 + \Delta x)^2 \]
\[= \frac{1}{4}\cdot(x_0^2 + 2 x_0 \Delta x + \Delta x^2) \]
\[= \frac{x_0^2}{4} + \frac{x_0\Delta x}{2} + \frac{\Delta x^2}{4} \]
Wir kriegen somit:
\[ \require{cancel} y'(x_0) = \lim_{\Delta x \rightarrow 0} \Big (\frac{\cancel{\frac{x_0^2}{4}} + \frac{x_0 \Delta x}{2} + \cancel{\frac{\Delta x^2}{4}} – \cancel{\frac{x_0^2}{4}}}{\Delta x} \Big ) \]
\[ \require{cancel} = \lim_{\Delta x \rightarrow 0} \Big (\frac{x_0 \cancel{\Delta x}}{2\cancel{\Delta x}} \Big ) = \frac{x_0}{2} \]
Die beiden \(\frac{x_0^2}{4}\) heben sich gegenseitig auf. Der Term \(\frac{\Delta x^2}{4}\) wird gestrichen, weil das ohnehin schon sehr, sehr kleine \(\Delta x\) quadriert wird, d.h. dadurch nochmals viel kleiner wird und deshalb vernachlässigt werden kann. Wir erhalten so die erste Ableitungsfunktion \(y'(x)\) von \(y(x)\):
\[ y'(x_0)=\frac{x_0}{2} \]
An der gesuchten Stelle \(x_0=2\) beträgt die Steigung der Funktion \(y(x)\) somit:
\[ y'(2)=\frac{2}{2} = 1 \]
Wir erhalten im Punkt A(2,1) eine Steigung von 1. Dieses Resultat bestätigt unsere Erwartung, dass die Steigung der Tangente kleiner sein muss, als die Steigung der Sekante, die wir ja mit 1.5 einfach berechnen konnten.
Beispiel
Bestimme die Steigung der Funktion \(y(x)=x^3\) an der Stelle \(x_0 = 1\).
Für den Differenzialquotienten brauchen wir folgende Grössen:
\[ f(x_0) = x_0^3 \]
\[ f(x_0 + \Delta x) = (x_0 + \Delta x)^3 \]
\[= x_0^3 + 3x_0^2\Delta x + 3 x_0 \Delta_x^2 + \Delta x^3 \]
Jetzt können wir den Differenzialquotienten aufstellen:
\[ y'(x_0) = \lim_{\Delta x \rightarrow 0} \Big (\frac{f(x_0 + \Delta x) – f(x_0)}{\Delta x} \Big ) \]
\[ \require{cancel} = \lim_{\Delta x \rightarrow 0} \Big (\frac{\cancel{x_0^3} + 3x_0^2\Delta x + 3 x_0 \cancel{\Delta_x^2} + \cancel{\Delta x^3} – \cancel{x_0^3}}{\Delta x} \Big ) \]
\[ = 3x_0^2 \]
An der Stelle \(x_0=1\) beträgt die Steigung also:
\[ y'(1) = 3\cdot1^2 = \underline{\;\;3\;\;} \]
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.