Rotation um die x-Achse
Wenn wir den Verlauf einer Funktion um die \(x\)-Achse rotieren lassen, entsteht ein Rotationskörper gemäss folgender Abbildung.
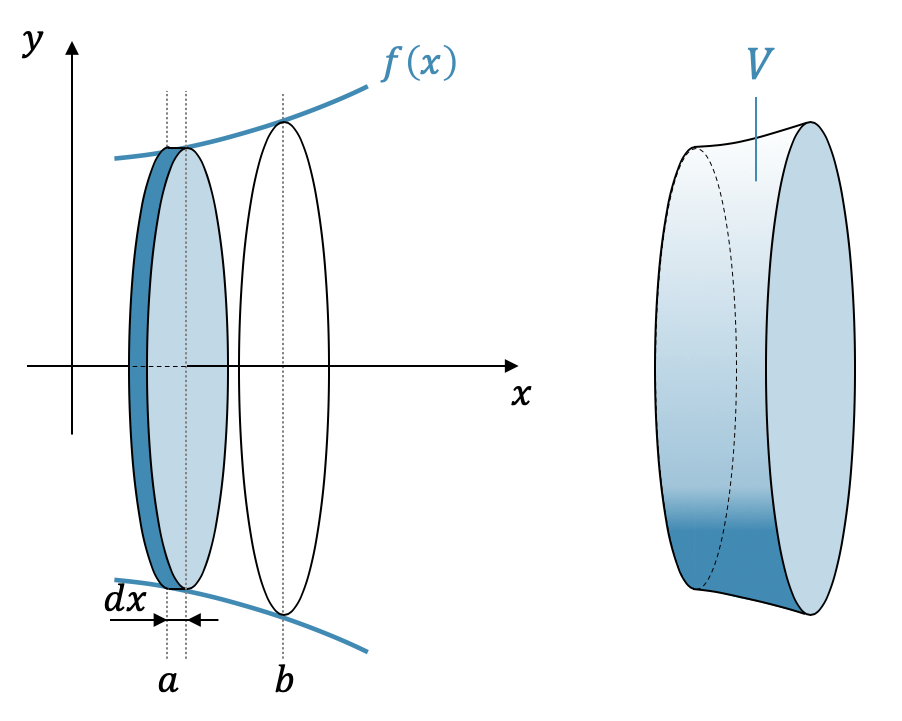
Mit Hilfe der Integralrechnung lässt sich das Volumen \(V\) dieses Körpers relativ einfach berechnen. Wir betrachten dazu eine unendlich dünne Scheibe (mit der Dicke \(dx\)). Es handelt sich dabei um einen Zylinder mit Radius \(r = f(x)\) und einer “Zylinderhöhe” von \(h=dx\). Für das Zylindervolumen schreiben wir: Volumen = Grundfläche (eines Kreises) mal Höhe.
\[ V_{\text{Zylinder}} = \pi r^2 h \]
Die infinitesimal dünne Scheibe (Dicke \(dx\)) hat ein infinitesimal kleines Volumen \(dV\):
\[ dV = \pi f(x)^2 dx \]
Um das ganze Volumen zu erhalten, müssen wir einfach über alle infinitesimalen Scheiben summieren, d.h. integrieren:
\[ V = \int dV \]
Wir setzen jetzt den Ausdruck für \(dV\) ein und lösen das Integral:
\[ V = \int_a^b \pi f^2(x)\;dx = \pi \int_a^b f^2(x)\;dx \]
Das Volumen eines Rotationskörpers um die \(x\)-Achse herum, beschrieben durch die Funktion \(f(x)\), berechnet sich mit dem folgenden Integral:
\[ V = \pi \int_a^b f^2(x)\;dx \]
Beispiel
Berechne das Volumen eines Kegels, der durch die Rotation von \(f(x)=x\) von \(0\) bis \(h\) entsteht.
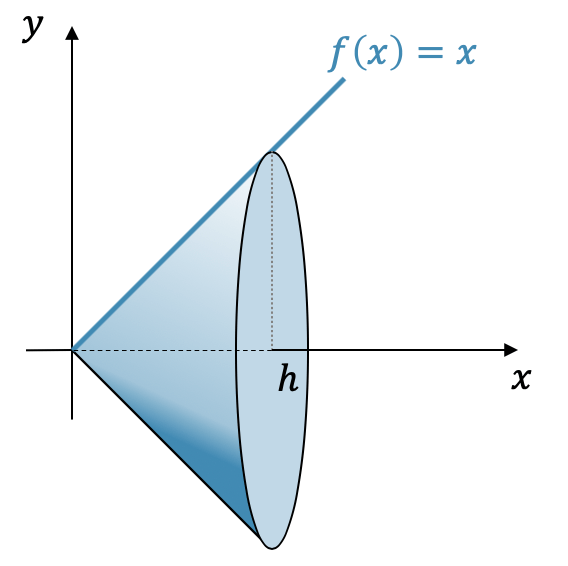
Wir benutzen die Formel für den Rotationskörper um die \(x\)-Achse herum und setzen \(f(x)=x\) und die Integrationsgrenzen \(0\) und \(h\) ein:
\[ V = \pi \int_0^h x^2\;dx = \pi \Big[ \frac{1}{3}x^3 \Big]_0^h \]
\[ \require{cancel} V = \frac{\pi}{3} \big( h^3 – \cancel{0^3} \big) = \;\; \underline{\frac{\pi h^3}{3}} \]
Rotation um die y-Achse
Wenn wir einen Rotationskörper um die \(y\)-Achse haben, können wir genau gleich vorgehen. Wir schauen uns das an einem Beispiel an.
Beispiel
Berechne den Rotationskörper um die \(y\)-Achse herum, der durch die Parabel \(f(x)=x^2\) erzeugt wird.
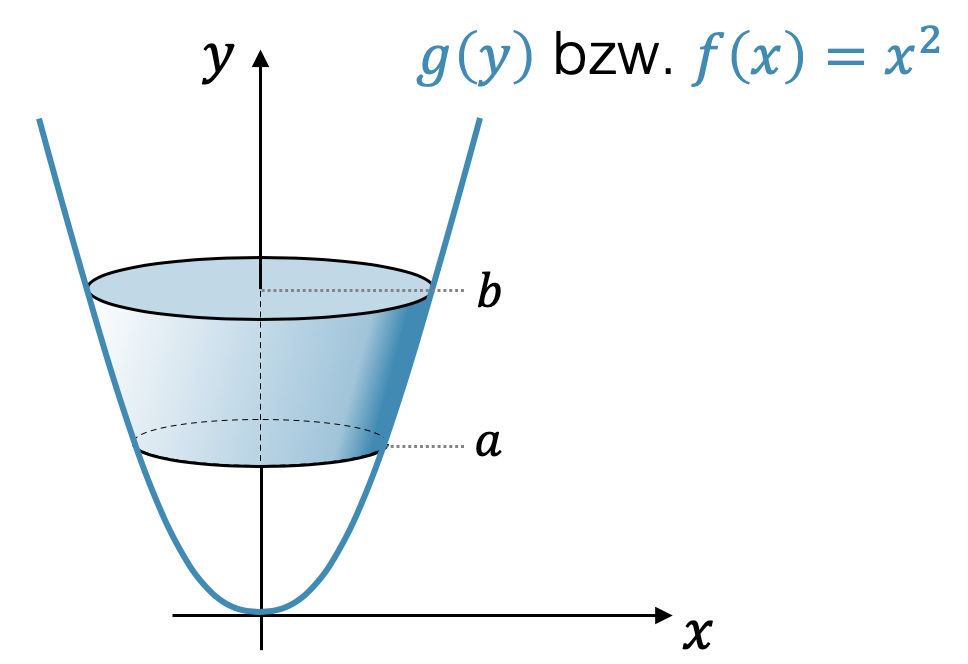
Zuerst versuchen wir die Formel für den Rotationskörper um die \(x\)-Achse zu gebrauchen, denn schliesslich ist das Volumen unabhängig davon, wie die Achse heisst oder in welche Richtung sie zeigt. Statt um die \(x\)-Achse herum, rotieren wir um die \(y\)-Achse herum, d.h. wir müssen einfach alles was \(x\) heisst mit \(y\) umbenennen:
\[ V = \pi \int f(x)^2\;dx \]
\[ \rightarrow \quad V = \pi \int_a^b g(y)^2\;dy \]
Das Problem ist nur, dass wir eine Funktion brauchen, deren Argument die Achse ist, um die wir rotieren. Für eine Rotation um die \(x\)-Achse ist es eine Funktion \(f\) von \(x\), für eine Rotation um die \(y\)-Achse ist es eine Funktion \(g\) von \(y\). Was ist die Funktion \(g(y)\), wenn wir \(f(x)=x^2\) haben? Es ist genau die Umkehrfunktion:
\[ y = x^2 \quad \leftrightarrow \quad \sqrt{y} = x \]
\[ g(y) = \sqrt{y} \]
Wir setzen dies ein in unser Integral für den Rotationskörper:
\[ V = \pi \int_a^b \big( \sqrt{y} \big)^2 \; dy = \pi \int_a^b y\; dy \]
\[ = \pi \Big[ \frac{1}{2}y^2 \Big]_a^b = \underline{\frac{\pi}{2} \big( b^2 – a^2 \big)} \]
Das Volumen eines Rotationskörpers um die \(y\)-Achse herum, beschrieben durch die Funktion \(g(y)\), berechnet sich mit dem folgenden Integral:
\[ V = \pi \int_a^b g^2(y)\;dy \]
Dabei ist \(g(y)=f^{-1}(y)\) die Umkehrfunktion von \(f(x)\):
\[ y = f(x) \quad \leftrightarrow \quad f^{-1}(y) = x \]
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.