Inhalt
Das Wichtigste in Kürze
Die 3 Keplerschen Gesetze bilden das Fundament für die Bewegung von Satelliten um ein Zentralobjekt herum, z.B. Planeten um die Sonne. Sie haben jedoch universelle Gültigkeit und können genauso gut für die Berechnung der Bewegung von Kometen um die Sonne oder von Satelliten um die Erde benutzt werden.
Das erste Gesetz besagt, dass die Umlaufbahnen der Satelliten Ellipsen sind und dass das Zentralobjekt in einem der beiden Brennpunkte liegt.
Das zweite Gesetz folgt aus der Erhaltung des Drehimpulses. Es beschreibt die Bahngeschwindigkeit in Abhängigkeit vom Abstand zum Zentralobjekt der Ellipse. Nahe zum Zentralobjekt (z.B. Sonne) ist der Satellit (z.B. Komet) schneller unterwegs als weit weg vom Zentralobjekt.
Das dritte Gesetz gibt uns die Möglichkeit die Umlaufperioden \(T\) zweier Satelliten mit ihren mittleren Abständen \(a\) zum Zentralobjekt in Relation zu setzen und daraus Berechnungen durchzuführen.
\[ \Big( \frac{T_1}{T_2} \Big)^2 = \Big( \frac{a_1}{a_2} \Big)^3 \]
Mit Hilfe des dritten Gesetzes konnte man aus den beobachteten Umlaufperioden erstmals die Abstände zu den Planeten unseres Sonnensystems berechnen.
Videos
Häufigste Fragen

Image by mana5280, shared on Unsplash
Anwendung der Keplerschen Gesetze
Johannes Kepler (1571 – 1630) war ein deutscher Naturphilosoph, Mathematiker, Astronom, Astrologe, Optiker und evangelischer Theologe und zählt zu den Begründern der modernen Naturwissenschaften.
Mit seinen drei Gesetzen konnte er als Erster die beobachtete Bewegung der Planeten erklären und berechnen. Seine Gesetze sind aber universell und gelten vom mikroskopischen Massstab bis hin zu den Bewegungen von ganzen Sternenhaufen.
Die drei Keplerschen Gesetze werden in erster Linie für die Bewegungen von Himmelsobjekten benutzt, die einzig durch die Gravitationskraft auf einander Einfluss nehmen. Sie beschreiben die Bewegung des Satelliten (z.B. Planet) auf seiner Bahn um ein Zentralobjekt (z.B. Sonne) herum:
- Keplers Erstes Gesetz: Die Bahnen sind geometrische Ellipsen, wobei der Kreis auch eine spezielle Ellipse ist.
- Keplers Zweites Gesetz: Aus der Drehimpulserhaltung folgt, dass die Geschwindigkeit abhängig vom Abstand zum Brennpunkt ist. Je näher der Satellit am Zentralobjekt ist, desto schneller bewegt er sich
- Keplers Drittes Gesetz: Die Umlaufperiode kann mit dem mittleren Radius der Bahn berechnet werden bzw. umgekehrt.
Im Endeffekt sind Keplers Gesetze eine direkte Folge des Drehimpulses von Punktmassen und seiner Erhaltung.
“Kreise sind auch Ellipsen. Beim Kreis fallen die beiden Brennpunkte im Kreiszentrum zusammen.”
Keplers Erstes Gesetz: Ellipsen
Das erste Gesetz besagt, dass die Bahn von Satelliten, die um ein Zentralobjekt “kreisen”, eine Ellipse ist. So ist die Bahn, auf welcher sich die Erde um die Sonne bewegt eine Ellipse. Die Bahn des Monds um die Erde ist ebenfalls eine Ellipse.
Ellipsen haben zwei Brennpunkte. Das Zentralobjekt steht in einem der beiden Brennpunkte: Der Schwerpunkt der Sonne steht in einem Brennpunkt der elliptischen Bahn der Erde. Der zweite Brennpunkt hat physikalisch keine physikalische Bedeutung.

Je weiter die Brennpunkte auseinander liegen, desto “schlanker” ist die Ellipse. Liegen die beiden Brennpunkte sehr nahe bei einander, ähnelt die Ellipse immer mehr einem Kreis.
Kreise sind auch Ellipsen. Beim Kreis fallen die beiden Brennpunkte im Kreiszentrum zusammen. Die Bahn der Erde ist fast kreisförmig und darf in guter Näherung als Kreis angesehen werden.
Wir wissen, dass Kreise sich dadurch auszeichnen, dass alle Punkte des Kreises den gleichen Abstand \(r\) zum Zentrum haben:
\[ r = \mathrm{konstant} \]
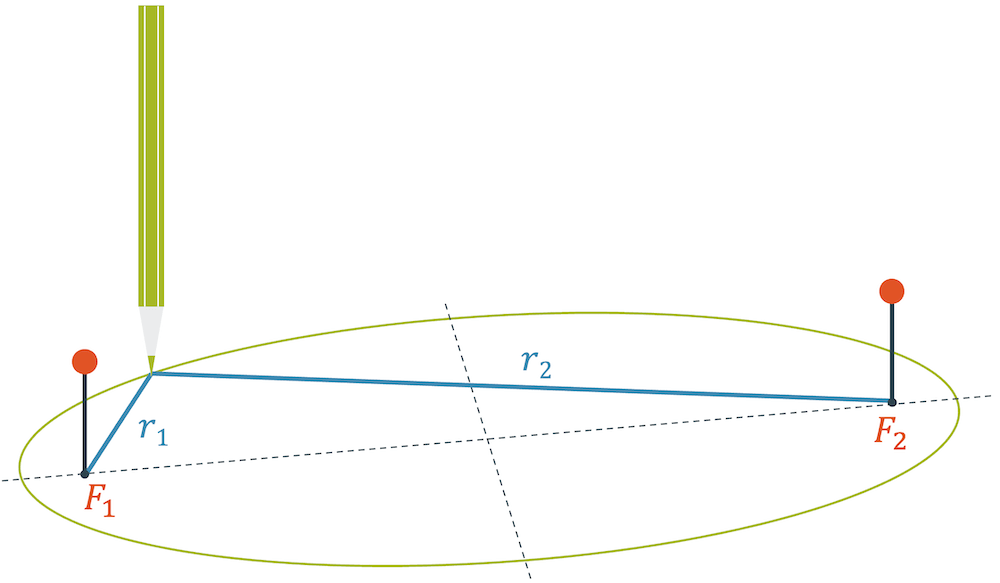
Ellipsen sind definiert dadurch, dass die Summe der beiden Abstände \(r_1\) und \(r_2\) zu den beiden Brennpunkten immer konstant ist:
\[ r_1 + r_2 = \mathrm{konstant} \]
Eine Ellipsen können wir konstruieren, indem wir einen Faden mit der konstanten Länge (\(r_1+r_2\)) nehmen und die beiden Fadenenden in den beiden Brennpunkten fixieren. Nun ziehen wir mit dem Bleistift am Faden, so dass er gespannt ist. Die beiden Teilstücke entsprechen \(r_1\) und \(r_2\) und sind in Summe immer gleich lang.
“Im Endeffekt sind Keplers Gesetze eine direkte Folge des Drehimpulses von Punktmassen und seiner Erhaltung.”
Keplers Zweites Gesetz: Drehimpulserhaltung
Wie die Energie oder der Impuls, so ist auch der Drehimpuls eine wichtige Erhaltungsgrösse. Es mag auf den ersten Blick erstaunen, aber eine Punktmasse, die sich mit der Geschwindigkeit \(v\) bewegt, hat auch einen Drehimpuls, selbst dann, wenn es keinerlei Drehbewegung gibt!
Der Drehimpuls \(L\) ist definiert als das Produkt des Trägheitsmoments \(I\) und der Winkelgeschwindigkeit \(\omega\):
\[ L = I \cdot \omega \]
Die Winkelgeschwindigkeit \(\omega\) ist mit der Bahngeschwindigkeit \(v\) verknüpft:
\[ v = r \cdot \omega \]
Das Trägheitsmoment für einen Massepunkt der Masse \(m\), mit Abstand \(r\) zum “Drehzentrum”, entnehmen wir aus einer Tabelle. Es gilt:
\[ I = m r^2 \]
Wir setzen beides ein für den Drehimpuls \(L\) und erhalten:
\[ L = m r^2 \cdot \frac{v}{r} = mrv \]
Aufgelöst nach der Bahngeschwindigkeit \(v\) erhalten wir:
\[ v = \frac{L}{m} \cdot \frac{1}{r} \]
Die Bahngeschwindigkeit ist somit umgekehrt proportional zum Abstand zum Brennpunkt.
Wenn ein Himmelskörper um die Sonne läuft, ist seine Geschwindigkeit abhängig vom Abstand zur Sonne. Kommt der Himmelskörper der Sonne näher, nimmt die Bahngeschwindigkeit zu. Umgekehrt wird der Himmelskörper bei zunehmendem Abstand von der Sonne immer langsamer.
Für die inneren Planeten (Merkur, Venus, Erde und Mars) sind die Bahnen praktisch kreisförmig, so dass dieser Effekt nicht sonderlich stark ins Gewicht fällt.
Asteroiden und v.a. Kometen haben oft sehr schlanke Ellipsen als Bahnen. Die Sonne ist in einem Brennpunkt, wo die Bahn ihr sehr nahe kommt. Der andere Brennpunkt ist sehr weit entfernt. ☄️
Kometen bewegen sich in der Nähe der Sonne, wo wir sie zu sehen bekommen, sehr schnell. Dann verschwinden sie wieder und werden immer langsamer auf ihrer sehr langen Bahn. Viele Kometen haben Umlaufperioden von Millionen von Jahren!
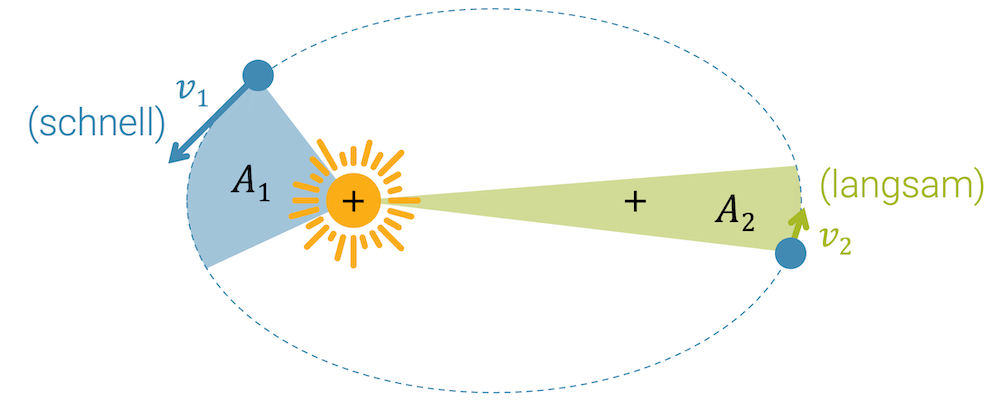
Keplers zweites Gesetz kann auch grafisch angewandt werden. Wir betrachten zwei Positionen auf der Bahn zwischen zwei Zeitpunkten. Diese beiden Punkte ergeben einen Bahnabschnitt, der abhängig ist von der Bahngeschwindigkeit. Die abgestrichene Fläche vom Brennpunkt zum Bahnabschnitt ist gemässe Kepler immer gleich gross:
\[ A_1 = A_2 \]
In kleinem Abstand ist die Bahngeschwindigkeit \(v_1\) gross, der Bahnabschnitt lang, dafür der Abstand \(r_1\) zum Brennpunkt relativ kurz. Der Bahnabschnitt ergibt eine Fläche \(A_1\).
Weit weg vom Brennpunkt ist die Bahngeschwindigkeit \(v_2\) viel kleiner und der Bahnabschnitt für die gleiche Zeitperiode somit kürzer. Dafür ist die Länge des “Kuchenstücks” relativ gross, so dass wir auch so zu der gleich grossen Fläche \(A_2\) kommen.
Keplers Drittes Gesetz: Periode & Abstand
Mit Hilfe des dritten Gesetzes können wir zwei verschieden grosse Bahnen um den gleichen zentralen Himmelskörper miteinander vergleichen. Insbesondere können wir die Umlaufperioden auf den beiden Bahnen berechnen.
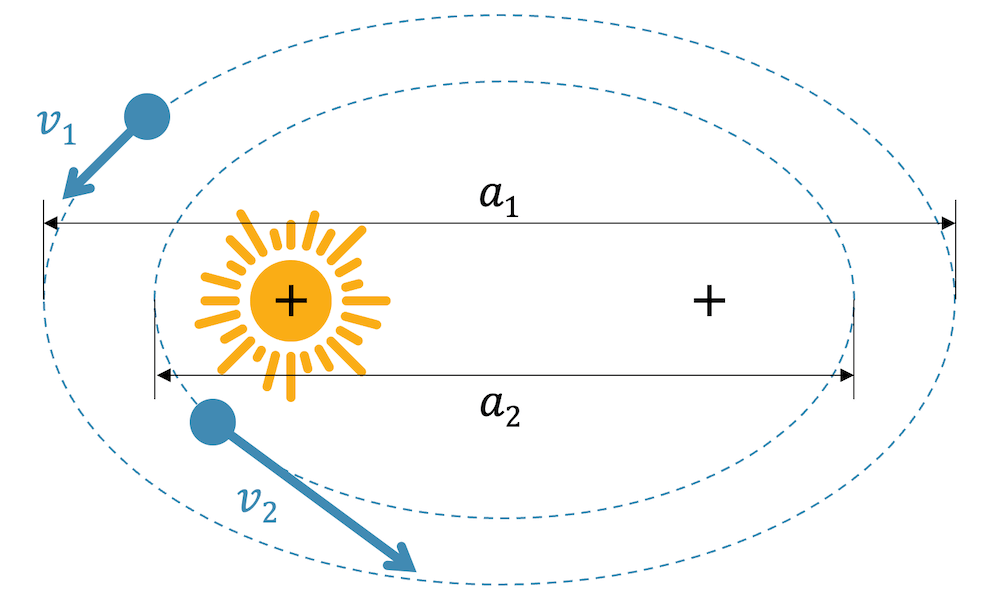
Wir werden auch dieses Gesetz nicht herleiten, sondern uns damit begnügen, das Gesetz anzuwenden. Wir betrachten zwei Bahnen mit den charakteristischen “Grössen” \(a_1\) und \(a_2\). Die beiden Umlaufperioden \(T_1\) und \(T_2\) stehen in einem Verhältnis, dass quadriert gleich dem Verhältnis der Grössen in der dritten Potenz entspricht:
\[ \Big( \frac{T_1}{T_2} \Big)^2 = \Big( \frac{a_1}{a_2} \Big)^3 \]
Beachte, dass wir bei Kreisbahnen die Grössen \(a_1\) nd \(a_2\) dem Durchmesser \(d_1\) bzw. \(d_2\) entsprechen, d.h. dem doppelten Radius.
Im Bruch können wir den Faktor 2 kürzen:
\[ \require{cancel} \frac{a_1}{a_2} = \frac{d_1}{d_2} = \frac{\cancel{2}\cdot r_1}{\cancel{2}\cdot r_2} \]
Beispiel: Keplers Drittes Gesetz
Unser Nachbarplanet, der Mars, braucht 687 Tage, um einmal um die Sonne zu wandern.
Wie gross ist der mittlere Abstand vom Mars zur Sonne in Astronomischen Einheiten?
(1 astronomical unit = 1 AU = mittlere Distanz zwischen Erde und Sonne).
Einfluss der Massen
Beachte, dass bei den Keplerschen Gesetzen die Masse nicht vorkommt, weder die Masse des Zentralobjekts, noch die Masse des Satelliten. Keplers Gesetze sind unabhängig von der Masse der Körper.
Der Effekt der Masse des Satelliten wird durch seine Trägheit wieder aufgehoben: Ein doppelt so schwerer Satellit wird einerseits doppelt so stark vom Zentralobjekt angezogen (Gravitationsgesetz). Andererseits ist der Satellit dann auch doppelt so träge. Die Zentripetalkraft ist doppelt so gross für die gleiche Kreisbewegung.
Deshalb fällt der Einfluss der Masse des Satelliten aus den Gleichungen wieder heraus.
Die Masse des Zentralobjekt finden wir auch nicht, obwohl sie eine Rolle spielt, nicht wie die Satellitenmasse.
Wie im Gravitationsgesetz beschrieben, spielt die Masse des Zentralobjekts eine wichtige Rolle für die Bahngeschwindigkeit des Satelliten: Je grösser die Masse des Zentralobjekts, desto schneller müsste der Satellit auf seiner Bahn sein, damit er nicht auf das Zentralobjekt abstürzt. Vergleiche dazu das Gedankenexperiment von Newton.
Bei Keplers Zweitem Gesetz vergleichen wir die Bahngeschwindigkeit des Satelliten an verschiedenen Stellen auf der Bahn um das Zentralobjekt. Kepler macht keine Aussage zur absoluten Geschwindigkeit. Dafür bräuchten wir die Masse des Zentralobjekts.
Bei Keplers Drittem Gesetz ist die Masse des Zentralobjekts ebenfalls eingebaut, aber durch den Vergleich von zwei Umlaufperioden und zwei Bahngrössen, die sich auf das gleiche Zentralobjekt beziehen, kürzt sich die Masse des Zentralobjekts wieder heraus und erscheint deshalb in den Keplerschen Gesetzen nicht.
Simulation
Aufgabensammlung
Lernziele
- Du kennst die drei Kepler’schen Gesetze und kannst Sie anwenden.
- Du kannst mit Hilfe des Dritten Keplerschen Gesetzes den mittleren Radius oder die Umlaufperiode eines Orbits berechnen. (analog zur Übung “Jupiter”)
Weitere Links
Keplersche Gesetze (Wikipedia)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt







Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.