Trägheitsmoment

Definitionen

Abkürzung: \(I\quad\) (manchmal auch \(J\;\))

Einheit: \([\,I\,] = {\text{kg m}}^2\)

Trägheitsmomente von geometrischen Körpern

Das Trägheitsmoment kann für jeden einigermassen geometrischen Körper berechnet werden. Je einfacher die Geometrie, desto einfacher die Rechnung – meist handelt es sich um ein Integral, das gelöst werden muss. Meistens reicht es aber aus, wenn der Körper mit Hilfe von geometrischen Körpern angenähert wird. Für diese Körper kann das Trägheitsmoment aus Tabellen entnommen werden. Nachfolgend ist eine solche Tabelle abgebildet.

Das Trägheitsmoment widerspiegelt die Masseverteilung bezüglich der Rotationsachse: Es ist umso grösser, je mehr Masse sich je weiter von der Rotationsachse befindet. Ein voller Zylinder hat ein Trägheitsmoment von \(I=\frac{1}{2}mr^2\). Machen wir den Zylinder hohl und verteilen die gleiche Masse nur auf den äussersten Mantel des Zylinders, so hat er bei gleicher Grösse und Masse ein doppelt so grosses Trägheitsmoment \(I=mr^2\). Seine Masse ist im Schnitt doppelt so weit von der Achse entfernt, wie die Masse des vollen Zylinders.

Beachten Sie, dass das Trägheitsmoment nicht nur von der geometrischen Form abhängig ist, sondern auch von der Anordnung der Rotationsachse: Ein Ring mit Masse \(M\) und Radius \(R\) hat ein Trägheitsmoment von \(I = MR^2\), wenn er um sein Zentrum rotiert. Lassen wir ihn aber um eine Achse rotieren, die in der Ringebene liegt, so ist sein Trägheitsmoment mit \(I = (\frac{1}{2}MR^2 + \frac{1}{2}Mw^2)\) deutlich kleiner, da \(w << R\).

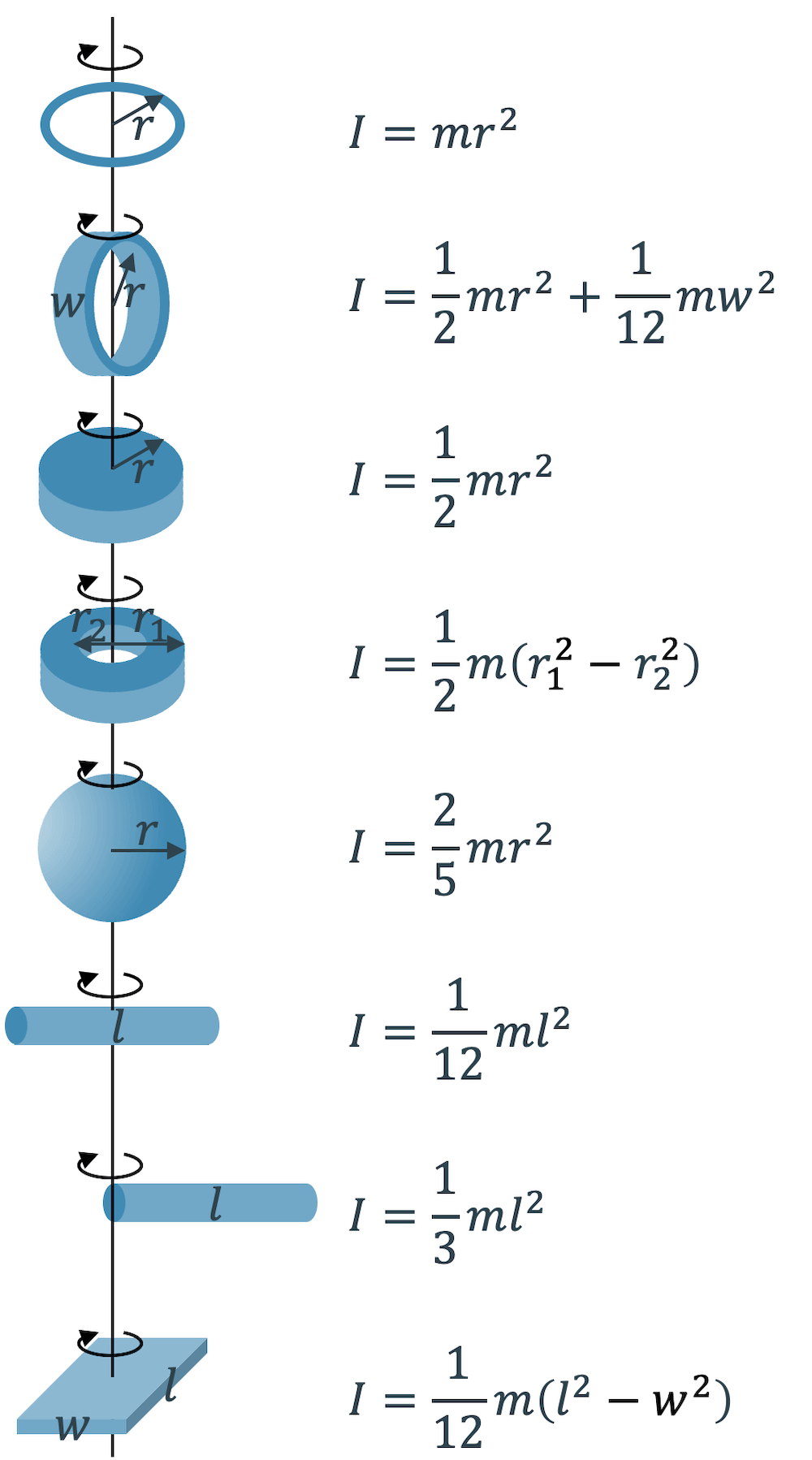
Beispiel

Für einen zylindrischen Aluminiumstab mit der Länge \(l=20\;\text{cm}\), dem Durchmesser \(d=1\;\text{cm}\) und der Masse \(m=43\;\text{g}\) sollen zwei Trägheitsmomente bestimmt werden.

---

Dieser Aluminiumstab hat nicht nur ein Trägheitsmoment, sondern ein für jede erdenkliche Rotationsachse. Zur Veranschaulichung betrachten wir zwei Fälle:

Rotieren wird den Stab um seine eigene Achse, so entnehmen wir der Tabelle das Trägheitsmoment für den vollen Zylinder:

\[ I_1 = \frac{1}{2}MR^2 = \frac{1}{2} \cdot m \cdot \big(\frac{d}{2}\big)^2 = \frac{1}{2} \cdot 0.43\;\text{kg} \cdot \Big(\frac{0.01\;\text{m}}{2}\Big)^2 = 5.4\cdot10^{-6}\;\text{kg m}^2 \]

Lassen wir aber den Stab quer um sein Zentrum rotieren, so beträgt das Trägheitsmoment:

\[ I_2 = \frac{1}{2}Ml^2 = \frac{1}{2} \cdot 0.43\;\text{kg} \cdot (0.2\;\text{m})^2 = 8.6\cdot10^{-3}\;\text{kg m}^2 \]

Dieses zweite Trägheitsmoment ist 1’600 mal grösser als das Trägheitsmoment um die eigene Achse!