
Schallgeschwindigkeit
Wir wissen, dass Überschallgeschwindigkeit höchstens von schnellen Flugzeugen und Raketen erreicht werden kann. Mit Überschallgeschwindigkeit ist eine Geschwindigkeit eines Objekts (in Luft) gemeint, die derjenigen der Schallwellen übersteigt. Die Schallgeschwindigkeit \(c\) ist abhängig der Dichte \(\rho\) des Gases und des Drucks \(p\):
\[ c = \sqrt{\kappa \cdot \frac{p}{\rho}} \]
Dabei ist \(\kappa\) der Adiabatenexponent. Für trockene Luft beträgt er \(\kappa = 1.402\). Bei üblichen Umgebungsbedingungen (trockene Luft, 20 °C) erhalten wir für die Schallgeschwindigkeit \(c\):
\[ c = 343.2\;\frac{\text{m}}{\text{s}} \]
Rechnen wir diese Geschwindigkeit in Kilometern pro Stunde um, erhalten wir:
\[ c = \frac{0.3432\;\text{km}}{\frac{1}{3600}\;\text{h}} = (0.3432 \cdot 3600)\;\frac{\text{km}}{\text{h}} \]
\[ c = 1’236\;\frac{\text{km}}{\text{h}} \]
Mach-Zahl
Ein Passagierflugzeug fliegt mit rund 850 bis 1000 Kilometern pro Stunde ganz klar unterhalb der Schallgeschwindigkeit. Das ist aber volle Absicht, denn bei Erreichen der Schallgeschwindigkeit ändert die Physik der Strömungen und das Flugzeug müsste komplett umgestaltet werden.
Weil die Schallwellen schneller als das Flugzeug sind, eilen sie vorne dem Flugzeug davon. Natürlich entsteht ein deutlicher Doppler-Effekt, mit verkürzten Wellenlängen vorne und verlängerten Wellenlängen hinter dem Flugzeug.
Um die Fluggeschwindigkeit mit der Schallgeschwindigkeit zu vergleichen, gibt es eine dimensionslose Kennzahl, die 1929 der Schweizer Aerodynamiker Jakob Ackeret eingeführt hat: die sog. Mach-Zahl. Sie ist benannt nach dem österreichischen Physiker und Philosophen Ernst Mach.
Die Mach-Zahl \(Ma\) ist der Anteil der Geschwindigkeit \(v\) eines Objekts an der Schallgeschwindigkeit des umgebenden Fluids \(c\) :
\[ Ma = \frac{v}{c} \]
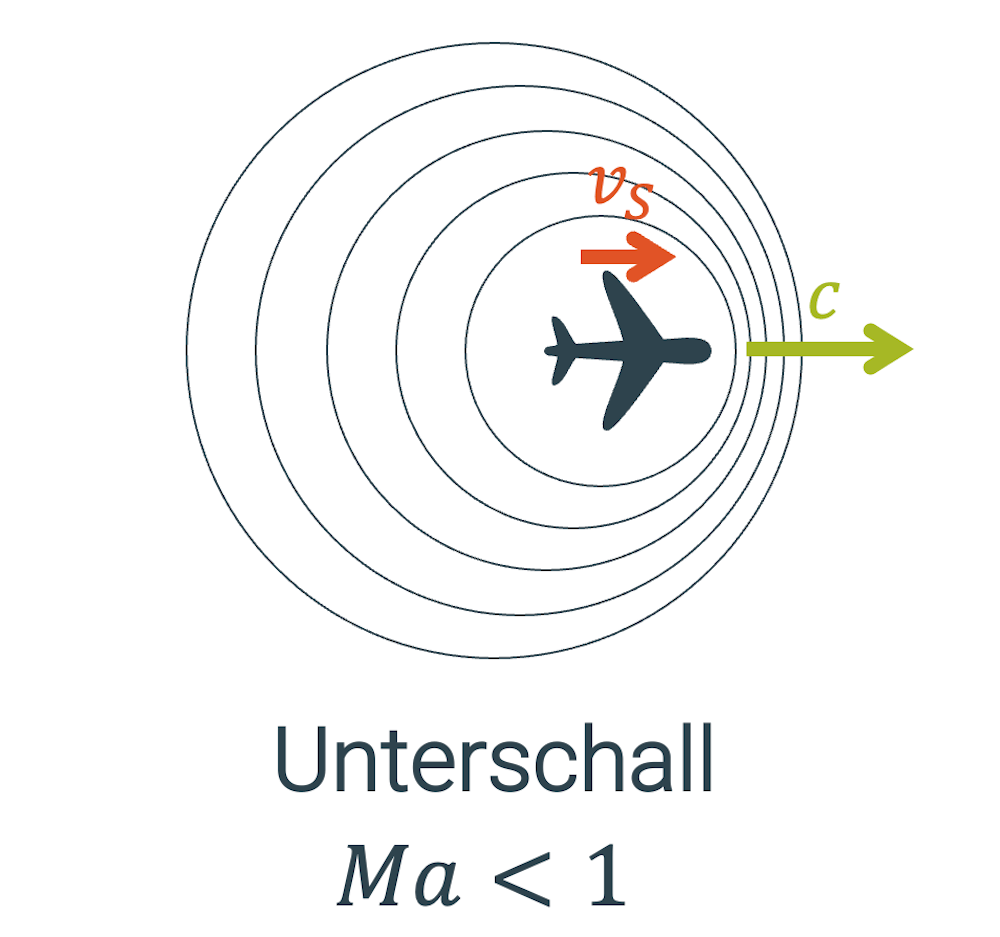
Sobald das Objekt die Schallgeschwindigkeit erreicht hat, werden die Wellen vor dem Objekt derart zusammengedrückt, dass sie nunmehr eine einzige Verdichtungsfront bilden. Die Mach-Zahl ist jetzt
\[ Ma = 1 \]
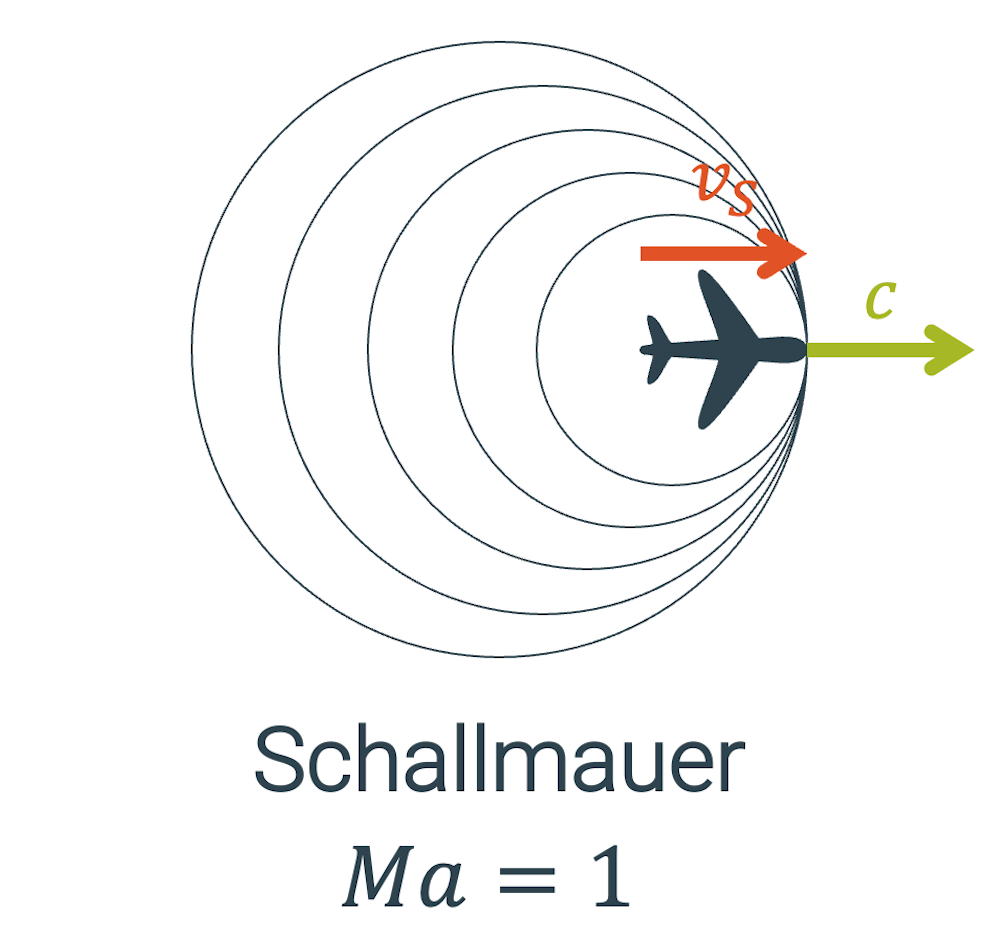
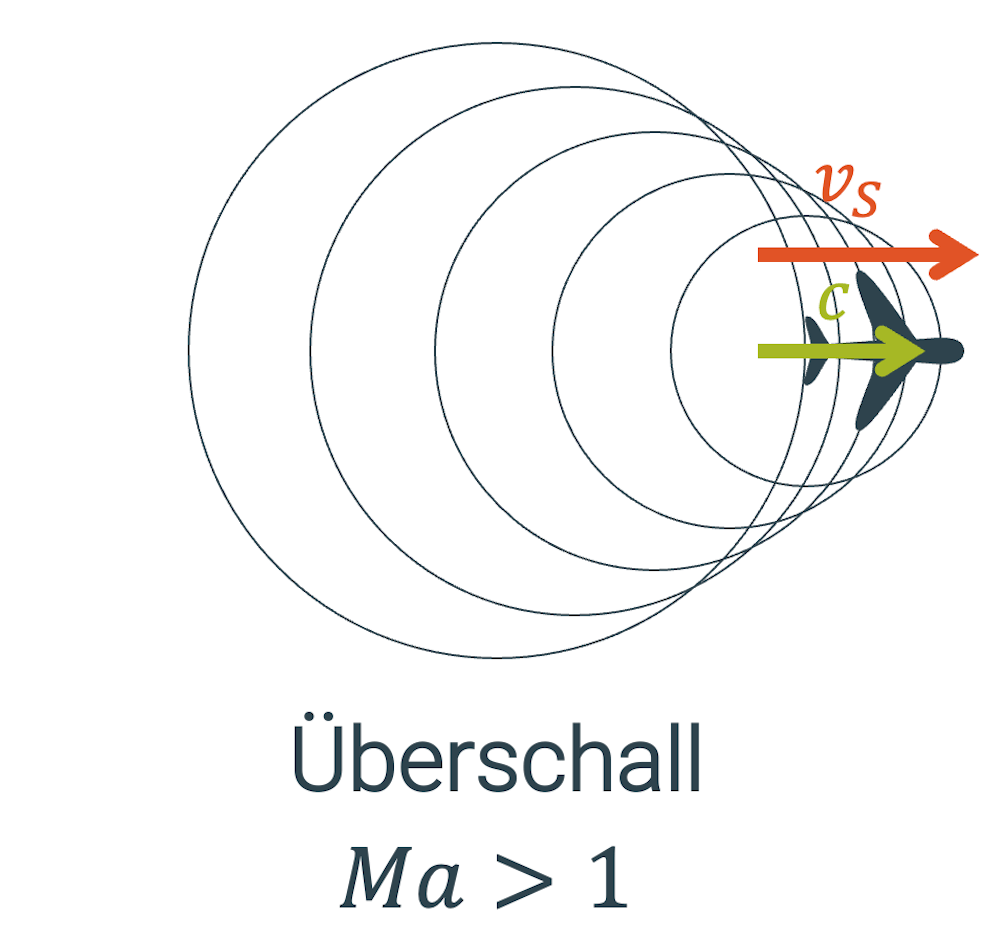
Übersteigt das Objekt die Schallgeschwindigkeit, spricht man auch vom Durchbrechen der Schallmauer. Die Mah-Zahl ist jetzt grösser als eins…
\[ Ma > 1 \]
…und das Flugzeug zieht die Druckstosswelle seitlich in Form eines Dreiecks bzw. sog. Mach-Kegels mit sich.
Ein Beobachter sieht zuerst das Flugzeug, das mit Überschallgeschwindigkeit fliegt. Es ist noch lautlos, da die Schallwellen den Beobachter noch nicht erreicht haben. Sobald die Druckstosswelle des Mach-Kegels den Beobachter auf der Erdoberfläche erreicht, hört er dieser einen Überschallknall. Das Flugzeug ist dann schon ein gutes Stückchen weiter gekommen.

Das nächste Mal, wenn Du eine Ente vorbei schwimmen siehst, wirst Du sicher an den Mach-Kegel denken. Die Ente schwimmt mit rund \(4\;\frac{\text{km}}{\text{h}}\) auf der Wasseroberfläche. Die Oberflächenwellen, die sie dabei erzeugt, sind sehr langsam. Die Wellengeschwindigkeit beträgt nur etwa \(2\;\frac{\text{km}}{\text{h}}\).
Die Ente schwimmt deshalb mit gewissermassen 2-facher Wellengeschwindigkeit!
Wir können an diesem Beispiel leider nicht die Mach-Zahl nehmen, weil es sich um eine Oberflächenwelle handelt und nicht um eine Schallwelle.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.