
Kopplung Schwingung – Welle
Schwingungen können Wellen aussenden, Wellen können Schwingungen erzeugen. Beide physikalischen Phänomene sind eng verwandt und miteinander gekoppelt. Am einfachsten können wir uns das mit einer Wasser-Oberflächenwelle vorstellen.
Eine Wellenfront auf dem Meer wandert mit ihrer Wellengeschwindigkeit. Eine Boje schwimmt an der Oberfläche und wird von der Welle erfasst. Die Welle bewegt die Boje auf und ab und zieht an ihr vorbei. Die Boje war kurzzeitig in Schwingung.

Der Unterschied zwischen der Welle und der Schwingung ist die Ortsabhängigkeit. Die Welle breitet sich im Raum mit der Zeit aus. Die Wellenfunktion ist deshalb eine Funktion vom Ort und der Zeit:
\[ y(x,t) \]
Bei der Schwingung interessieren wir uns nur für die “Schwimmhöhe” der Boje. Horizontal gesehen, ist die Boje an einer fixen Position \(x_0\), da sie mit einer Kette am Meeresgrund befestigt ist. Wir kriegen die Schwingungsfunktion, wenn wir die örtliche Variable weglassen (weil sie ja nicht mehr variabel, sondern fix \(x=x_0\) ist) und nur noch die Abhängigkeit von der Zeit betrachten:
\[ y(x_0,t) = y(t) \]
Im folgenden Diagramm schauen wir uns die Position der Boje \(x_0\) in der Momentaufnahme der Welle zum Zeitpunkt \(t=0\) an: \(y(x,0)\). Die Boje ist gerade auf der Höhe “null”.
\[ y(x_0,0) =0 \]
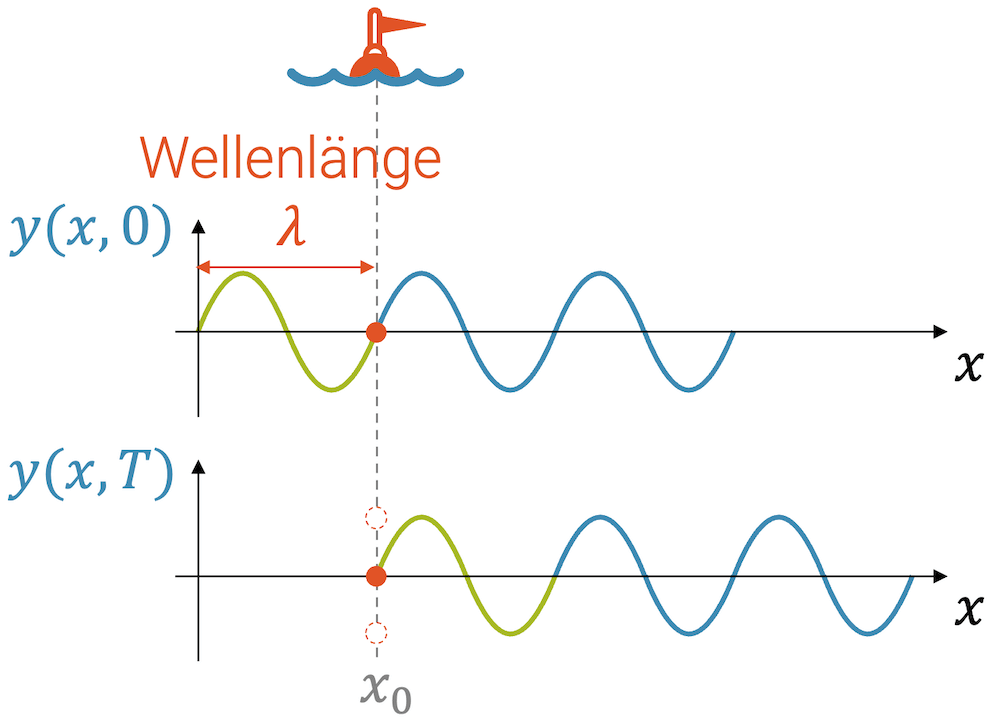
Wenn wir jetzt eine Periode \(T\) lang warten, dann zieht die Welle (grüner Teil) an der Boje vorbei. Die Welle bewegt die Boje zuerst nach unten, dann nach oben und bringt sie schliesslich wieder zur Höhe “null”. Im unteren Diagramm haben wir dann die Wellensituation zum Zeitpunkt \(T\): \(y(x,T)\) und für die Boje:
\[ y(x_0,t=T) = 0 \]
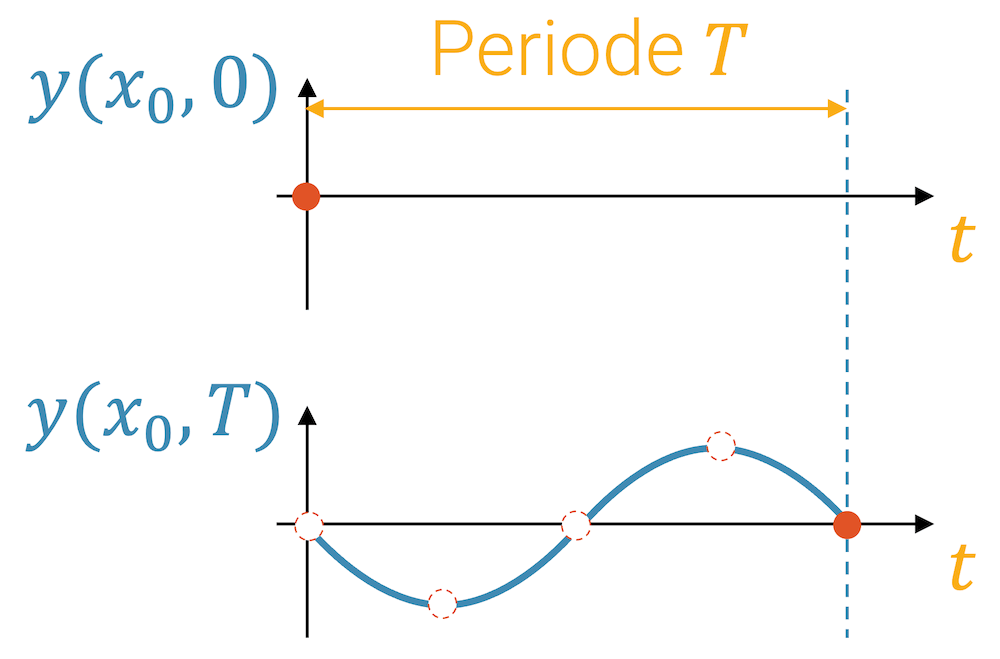
Was ist passiert? Während der Periode \(T\) ist genau eine Wellenlänge \(\lambda\) an der Boje vorbeigezogen. Das hat sie natürlich mit der Wellengeschwindigkeit \(c\) gemacht. Wir können deshalb schreiben, dass die Wellengeschwindigkeit der zurückgelegten Strecke \(\lambda\) in der Zeit \(T\) entspricht:
\[ c = \frac{\lambda}{T} \]
Jetzt wissen wir, dass die Periode gleich dem Kehrwert der Frequenz ist: \(T = \frac{1}{f}\) bzw. \(f = \frac{1}{T}\). Oben eingesetzt ergibt das:
\[ c = \lambda \cdot f \]
Frequenz \(f\), Wellenlänge \(\lambda\) und Wellengeschwindigkeit \(c\) sind über die Beziehung:
\[ c = \lambda \cdot f \]
oder
\[ c = \frac{\lambda}{T} \]
verknüpft, wobei \(T\) der Periode entspricht. Somit erzeugt eine Schwingung mit Frequenz \(f\) eine Welle mit \(\lambda\) und \(c\) bzw. eine solche Welle erzeugt wieder eine Schwingung mit Frequenz \(f\).
Wenn die Welle aus irgendeinem Grund schneller werden sollte, dann werden die Wellenkämme auseinander gezogen und die Wellenlänge vergrössert sich.
Harmonische Wellenfunktion
Es gibt Wellen, die nur einen Impuls enthalten, der sich mit Wellengeschwindigkeit fortbewegt. Solche Wellen werden durch ein entsprechend impulsartiges Ereignis ausgelöst. Wenn wir ein Steinchen ins Wasser werfen, erzeugt der “Einschlag” zur Bildung einer Wasser-Oberflächenwelle, die sich kreisförmig fortbewegt.
Wenn wir aber eine harmonische Schwingung als Quelle haben, dann erzeugt diese Schwingung eine ebenfalls harmonische Welle, d.h. eine Welle, die zu jedem Moment mit einer Sinusfunktion beschrieben werden kann.
Ein solcher Sinus hat eine Periode von \(2\pi\). Wie kommen wir zu einer Sinusfunktion, die die Periode hat, die der Wellenlänge \(\lambda\) entspricht? Wir stauchen zuerst die Sinusfunktion in horizontaler Richtung mit dem Faktor \(2\pi\), so dass wir eine verkürzte Periode von 1 erhalten.
Das erreichen wir, indem wir statt dem Argument \(x\), neu das Argument \(2\pi x\) in den Sinus einsetzen. Wenn z.B. \(x\) nur \(\frac{1}{4}\) als \(x\)-Wert haben, dann gehen aber \(2\pi \cdot \frac{1}{4} = \frac{\pi}{2}\) in den Sinus. Wir sind dann genau beim Maximum bzw. bei einem Viertel der Periode.
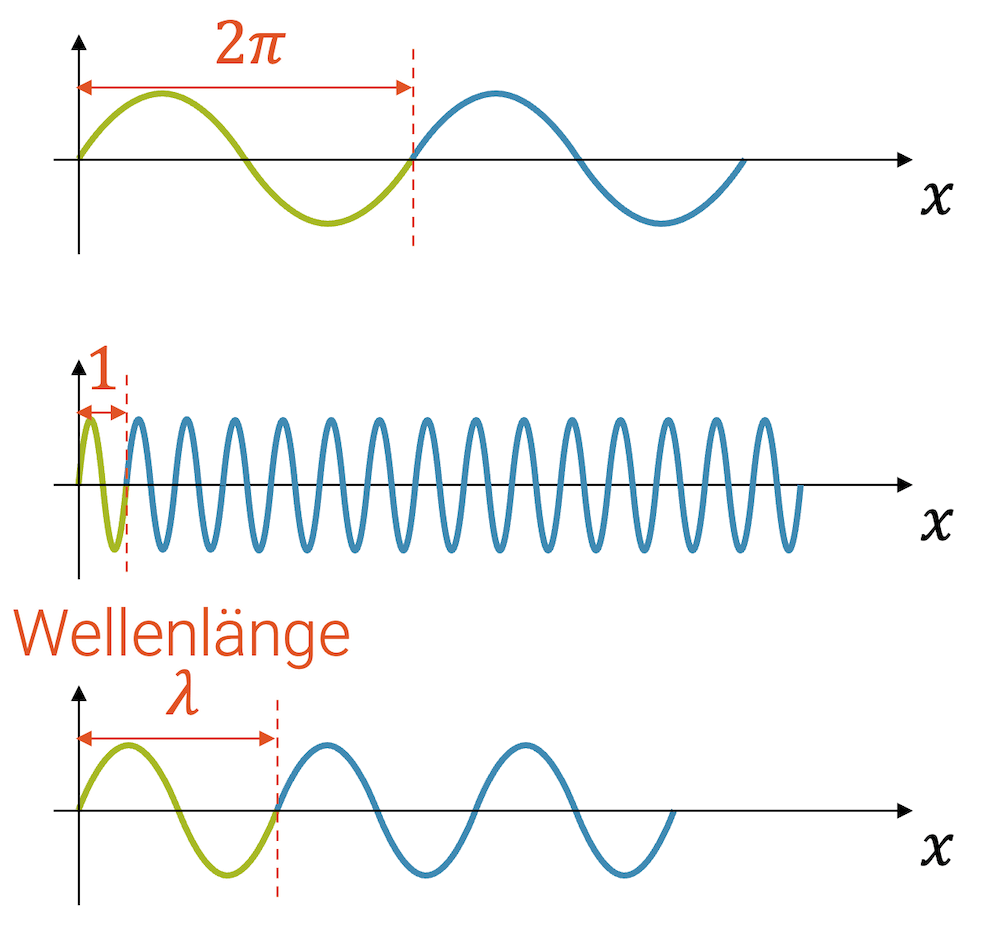
In gleicher Art strecken wir jetzt die Sinusfunktion horizontal und erhalten so:
\[ y(x,0) = A \cdot \sin\Big( \frac{2\pi x}{\lambda} \Big) \]
Um die Sache etwas übersichtlicher zu gestalten, machen wir folgende Substitution:
\[ k = \frac{2\pi}{\lambda} \]
Diese Zahl \(k\) wird auch Wellenzahl genannt. Die Funktion vereinfacht sich damit zu:
\[ y(x,0) = A \cdot \sin (kx) \]
Jetzt haben wir aber nur einen statischen Sinusverlauf über die \(x\)-Achse mit Wellenlänge \(\lambda\). Wir müssen sie jetzt noch in Bewegung versetzen. Wenn wir genau eine Periode \(T\) abwarten, verschiebt sich die Welle um eine Wellenlänge \(\lambda\). Wir wählen jetzt mal die positive \(x\)-Richtung und verschieben die Funktion horizontal nach rechts, indem wir das Argument \(x\) mit \((x-\lambda)\) ersetzen:
\[ y(x,T) = A \cdot \sin \big( k \cdot (x-\lambda) \big) \]
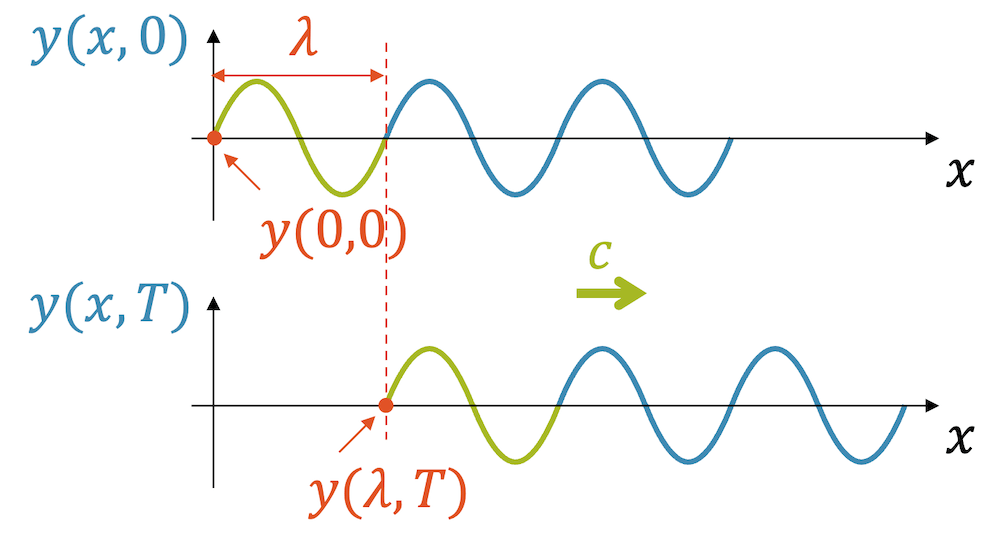
Hätten wir zwei Perioden lang gewartet, wäre die Welle um zwei Wellenlängen gewandert, nach drei Perioden um drei Wellenlängen usw. Wir können deshalb die Verschiebung verallgemeinern mit dem \(\frac{t}{T}\)-Vielfachen von \(\lambda\):
\[ y(x,t) = A \cdot \sin \big( k \cdot (x – \frac{t}{T} \lambda) \big) \]
\[ y(x,t) = A \cdot \sin \big( kx – k \frac{t}{T} \lambda \big) \]
Das können wir noch ein bisschen aufräumen, indem wir \(T = \frac{1}{f}\) und \(\omega = 2\pi f\) verwenden:
\[ k \cdot \frac{t}{T} \cdot \lambda = k \cdot tf \cdot \lambda = k \lambda \cdot \frac{\omega}{2\pi} \cdot t \]
\[ \require{cancel} = \Big(\frac{\cancel{2\pi}}{\cancel{\lambda}}\Big) \cancel{\lambda} \cdot \frac{\omega}{\cancel{2\pi}} \cdot t = \omega t \]
Wir können also schreiben:
\[ y(x,t) = A \cdot \sin \big( k x – \omega t \big) \]
Die Funktion einer periodischen Welle ist eine Funktion des Ortes \(x\) und der Zeit \(t\). Sie entspricht einem Sinusverlauf, der in der räumlichen \(x\)-Dimension eine Wellenlänge \(\lambda\) hat. Die Welle bewegt sich mit der Wellengeschwindigkeit \(c\), was bedeutet, dass in der zeitlichen Periode \(T\) sich die Welle genau um \(\lambda\) fortbewegt.
\[ y(x,t) = A \cdot \sin \big( k x – \omega t \big) \]
Dabei ist \(A\) die Amplitude der Welle, \(k=\frac{2\pi}{\lambda}\) die Wellenzahl und \(\omega\) die Frequenz der Welle bzw. Schwingung an einem fixen Punkt.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.