
Entstehung des Doppler-Effekts
Der Doppler-Effekt wird nach Christian Doppler (1803 – 1853), einem österreichischem Mathematiker und Physiker benannt. Aus unserer heutigen Sicht ist es erstaunlich, dass zu Dopplers Lebzeiten, das Pferd noch das schnellste Fortbewegungsmittel war! Mit der Erfindung der Eisenbahn wurden erstmals Geschwindigkeiten erreicht, die den Doppler-Effekt merkbar machen.
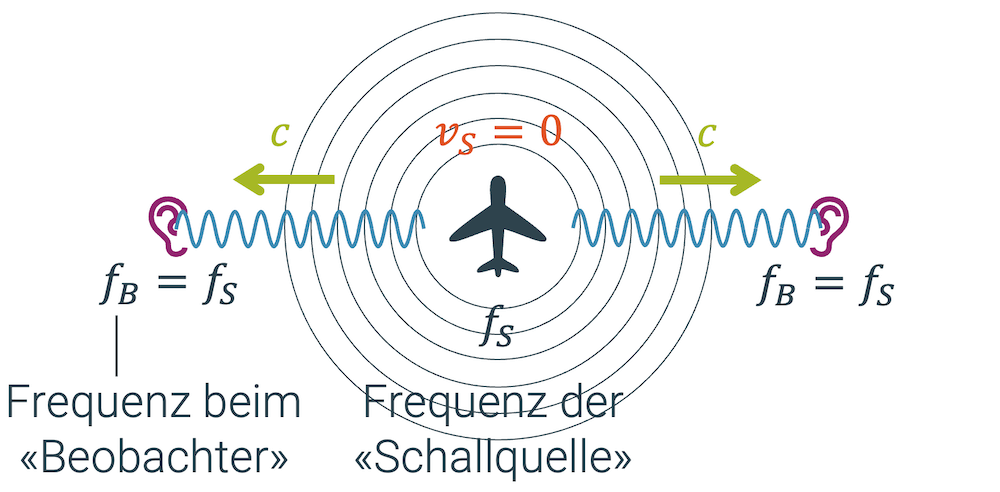
Wenn eine Schallquelle still steht (\(v_S = 0\)), bewegen sich die Schallwellen mit Wellengeschwindigkeit \(c\) von der Schallquelle weg. Die Frequenz der Schallquelle \(f_S\) ist auch die Frequenz, die der Beobachter empfäng bzw. hört:
\[ f_B = f_S \]
Bewegte Quelle
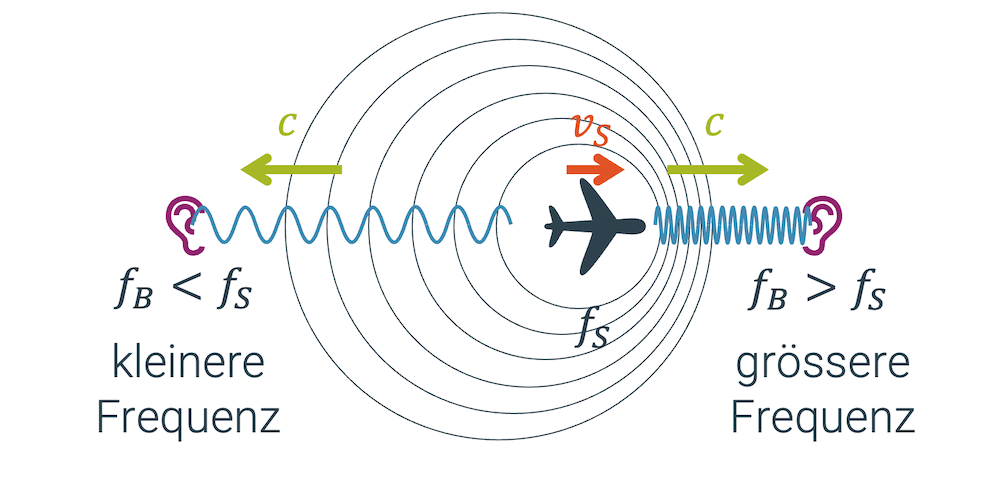
Wird die Schallquelle bewegt (\(v_S>0\)), so werden die Wellenlängen in Wegrichtung der Schallquelle zusammengedrängt, d.h. sie werden kürzer. Die Wellenlängen hinter der Schallquelle werden gestreckt. Die Schallwellen bewegen sich noch immer mit der gleichen Wellengeschwindigkeit \(c\).
Wir können uns das so vorstellen. Wir tippen mit dem Finger auf die Wasseroberfläche und sehen die kreisförmigen Wasserwellen weggehen. Wenn wir mit dem Finger immer ein bisschen mehr nach rechts tippen, verschieben wir das Zentrum der Kreise immer mehr nach rechts. Tatsächlich entstehen rechts engere Wellenkämme und links sind sie weiter auseinander.
Jetzt wenden wir die Beziehung zwischen der Wellengeschwindigkeit \(c\) und der Wellenlänge \(\lambda\) an:
\[ c = \lambda \cdot f \]
Aufgelöst nach der Frequenz gibt das:
\[ f = \frac{c}{\lambda} \]
Wenn die Schallgeschwindigkeit \(c\) für alle Schallwellen in alle Richtungen gleich ist, die Wellenlängen links aber grösser sind, dann wird ein Beobachter links eine kleinere Frequenz \(f_B<f_S\) erfahren, d.h. er hört einen tieferen Ton. Der Beobachter rechts wird eine höhere Frequenz vernehmen, als die Schallquelle effektiv abgibt (\(f_B>f_S\)).
Wenn wir beispielsweise an einem Fussgängerstreifen stehen und die Autos an uns vorbeifahren, dann hören wir immer einen “Wrummm”-Ton, der von hoch zu tief wechselt. Noch eindrücklicher ist es mit einer Sirene, die an uns vorbeifährt. Ihr Ton ist beim sich Nähern hoch und beim Wegfahren tief. In Wirklichkeit ist der emittierte Ton natürlich immer gleich hoch. Die Frequenzunterschiede, die der Beobachter hört, sind auf den Doppler-Effekt zurückzuführen.
Herleitung
Wir werden hier den klassischen Fall der bewegten Schallquelle anschauen: Die bewegte Schallquelle und der ruhende Beobachter (fahrender Wagen mit Sirene). Die Herleitung der anderen Fälle erfolgt analog.
Die Schallquelle gibt im Stillstand eine Welle der Länge \(\lambda_S\) ab. Für den Beobachter wird diese Wellenlänge verkürzt, weil sich die Schallquelle mit der Geschwindigkeit \(v_S\) dem Beobachter nähert. In einer Periode \(T\) verkürzt sich die Wellenlänge um den Weg, den die Schallquelle in dieser Zeit zurücklegt:
\[ \Delta \lambda = v_S \cdot T \]
Damit ist die vom Beobachter empfangene Wellenlänge \(\lambda_B\):
\[ \lambda_B = \lambda_S – v_S \cdot T \]
Jetzt können wir mit der Beziehung \(c = \lambda \cdot f\) die Wellenlängen mit den Frequenzen ersetzen:
\[ \frac{c}{f_B} = \frac{c}{f_S} – v_S \cdot T \]
Für die Periode \(T\) setzen wir den Kehrwert der Frequenz ein (\(T=\frac{1}{f_S}\)). Nach \(f_B\) aufgelöst, erhalten wir:
\[ f_B = \frac{c}{\big(\frac{c}{f_S}\big) – \big(v_S \cdot \frac{1}{f_S}\big)} \]
\[ f_B = \frac{c}{\frac{1}{f_S} \cdot (c-v_S)} \]
\[ f_B = f_S \cdot \frac{c}{c – v_S} \]
Damit haben wir die vom Beobachter empfangene Frequenz \(f_B\) in Abhängigkeit der Geschwindigkeit der Schallwelle \(f_S\). Wir sehen auch, dass unsere Formel nur bis für Geschwindigkeiten der Schallwelle unterhalb der Schallgeschwindigkeit gültig ist. Sobald die Schallquelle die Schallgeschwindigkeit erreicht, werden die Schallwellen zusammengedrückt, so dass ihre Wellenlänge eigentlich null beträgt.
Verschiedene Situationen mit Doppler-Effekt
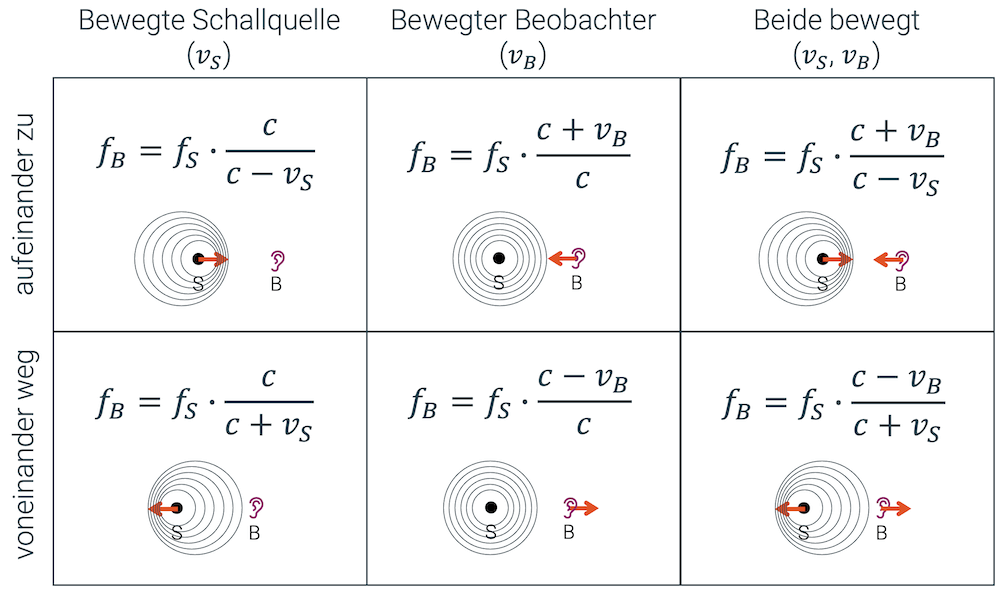
Die Situation der bewegten Schallquelle am Beispiel eines Sirenenwagens ist die bekannteste Form des Doppler-Effekts. In der nachfolgenden Tabelle ist dieser Fall mit den beiden Ausprägungen in der linken Spalte festgehalten.
Statt einer bewegten Schallquelle gibt es auch den bewegten Beobachter (mittlere Spalte). Ein Beispiel dafür ist das Vorbeifahren an einem Ton, z.B. der Zug, der an einem Bahnübergang mit Haltesignal vorbeifährt. Auch hier wird der Beobachter zuerst eine hohe und dann eine tiefere Frequenz vernehmen.
Schliesslich gibt es natürlich noch den Fall, in welchem beide sich bewegen: Die Schallquelle geht auf den Beobachter zu oder geht von ihm weg (rechte Spalte).
Warum wird zwischen einer bewegten Schallquelle und einem bewegten Beobachter unterschieden? Das ist gar nicht so offensichtlich, denn aus der Kinematik wissen wir, dass bei zusammengesetzten Bewegungen es reicht, die Relativgeschwindigkeit anzuschauen: Mit welcher Geschwindigkeit bewegen sich die beiden aufeinander zu oder voneinander weg?
Beim Doppler-Effekt reicht allein die Relativgeschwindigkeit nicht, denn die Luft als Übertragungsmedium muss berücksichtigt werden. Wenn ein Krankenwagen auf uns mit 50 km/h zufährt, dann sind Beobachter und Luft in Ruhe. Wenn der Beobachter mit 50 km/h an der Schallquelle vorbeifährt, dann sind dieses Mal Schallquelle und Luft in Ruhe.
Doppler-Effekt ohne Medium
Christian Doppler vermutete, dass der von ihm beschriebene Effekt sich wohl auch auf andere Wellenarten übertragen lässt. Wenn bei Schallwellen die Frequenz die Höhe des Tons ausmacht, so bestimmt die Frequenz bei elektromagnetischen Wellen die Art der Welle und bei Lichtwellen die Farbe.
Tatsächlich wird in der Astronomie sehr viel mit der sog. Rotverschiebung bzw. dem Gegenstück Blauverschiebung gearbeitet. Wir können bei gewissen Rotverschiebungen auf die Geschwindigkeit der Lichtquelle (Sterne bzw. Galaxien) schliessen.
Im Gegensatz zum Doppler-Effekt von Schallwellen, brauchen elektromagnetische Wellen kein Medium für deren Übertragung, so dass wir hier mit der Relativgeschwindigkeit arbeiten können. Es kommt nicht darauf an, ob sich der Beobachter bewegt oder die Quelle, sondern nur wie sie sich relativ zueinander bewegen.
Der Doppler-Effekt für elektromagnetische Wellen wird auch der Medizin verwendet, um z.B. die Fliessgeschwindigkeit in Blutgefässen zu messen. Eine andere Anwendung ist das Feststellen von Geschwindigkeitsübertretungen durch Radarfallen.
Eine unsichtbare elektromagnetische Welle wird zum fahrenden Fahrzeug geschickt, wo sie zurückreflektiert wird. Wenn das Fahrzeug also elektromagnetische Wellen wieder zurückschickt, handelt es wie eine bewegte Quelle von elektromagnetischer Strahlung.
Steht die Radarfalle vor dem Fahrzeug, sind die ankommenden Wellen in ihrer Wellenlänge verkürzt und der Sensor kann aufgrund der Frequenzdifferenz die Fahrzeuggeschwindigkeit berechnen. Das Ganze funktioniert auch bei einem Radar hinter dem Fahrzeug. Hier wird die Wellenlänge verlängert (bzw. die Frequenz verkleinert).
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.