
Beschreibung von harmonischen Schwingungen
Harmonische Schwingungen haben den charakteristischen sinus-förmigen Verlauf über die Zeit. Natürlich könnte auch der Kosinus eingesetzt werden, denn dieser unterscheidet sich vom Sinus nur darin, dass er dem Sinus um einen Viertel einer Periode voraus ist.
Wie im einleitenden Artikel zu den Schwingungen beschrieben, entsteht eine Schwingung, wenn eine Trägheit mit einer rückstellenden Grösse kombiniert werden. In mechanischen Systemen ist die Trägheit meistens durch die Masse gegeben und die rückstellende Grösse ist die sog. Rückstellkraft.
“Eine harmonische Schwingung entsteht nur dann, wenn die Rückstellkraft genau proportional ist zu der Auslenkung.”
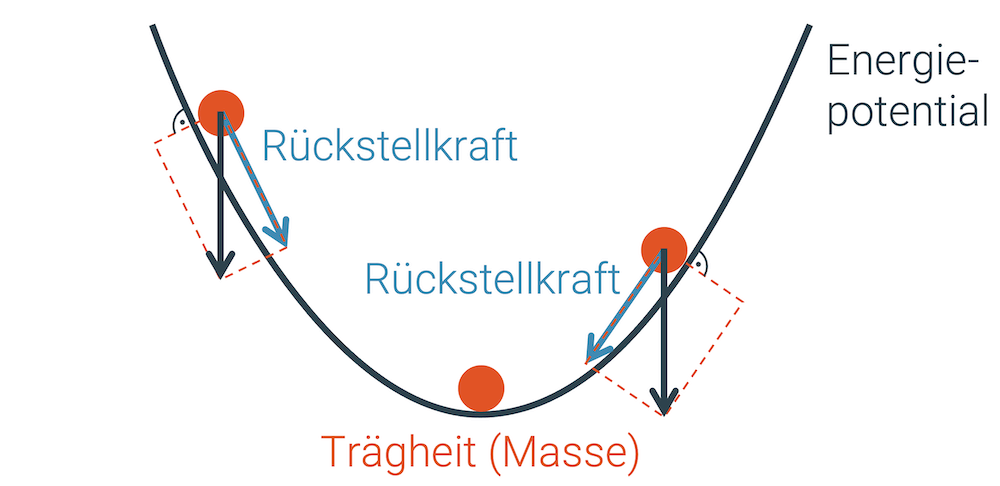
Wenn die Rückstellkraft genau proportional ist zur eigentlichen Auslenkung, entsteht eine harmonische Schwingung, die mathematisch mit einem Sinus beschrieben werden kann.
Ist diese genaue Proportionalität nicht gegeben, wird das System trotzdem schwingen, aber die Schwingung wird keinen Sinusverlauf zeigen und gilt deshalb nicht als harmonisch.
Experiment: Federpendel und Kreisscheibe
Ein bekanntes Physik-Experiment demonstriert sehr schön, dass ein vertikales Federpendel tatsächlich eine harmonische Schwingung macht. Der Schatten der schwingenden Masse bewegt sich auf und ab, treu zu einem Sinus. Dass dem so ist, kann mit einem zweiten Schatten gezeigt werden, nämlich dem Schatten einer gleich grossen, an einer Drehscheibe befestigten Masse.
Im Experiment sind die Frequenzen der Schwingung des Federpendels und diejenige der Kreisbewegung perfekt abgestimmt. Wir können beobachten, wie beide Schatten schön synchron auf- und abbewegen.
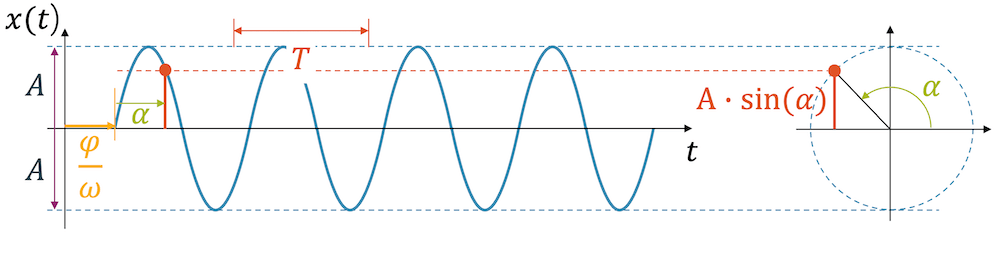
Warum beweist das den sinusförmigen Verlauf? Der Schatten der Masse auf der Kreisscheibe übernimmt die “Höhe” oder \(y\)-Koordinate der kreisenden Masse. Wir erinnern uns, dass diese Höhe im Einheitskreis genau dem Sinus des Winkels \(\alpha\) entspricht. Wenn die Kreisscheibe nun einen Radius \(A\) hat, dann ist die Schattenbewegung entsprechend um den Betrag \(A\) multipliziert. Es ist die Amplitude unserer Schwingung.
Herleitung der Eigenfrequenz
Wir werden hier die Eigenfrequenz \(\omega_0\) eines Federpendels herleiten und sehen, wie ein harmonisches Schwingungssystem mathematisch beschrieben wird. Ein Federpendel besteht aus einer trägen Masse \(m\), die an eine Feder mit Federkonstante \(k\) befestigt ist.
Wenn die Feder mit einer Kraft auf die Masse wirkt, beschleunigt sie diese. Das physikalische Gesetz dazu ist Newtons Zweites Gesetz:
\[ F = m \cdot a \]
Da wir die Position der Masse als Schwingung beschreiben möchten, legen wir die \(x\)-Achse in die Bewegungsrichtung unserer Masse und beschreiben ihre Position mit einer Funktion der Zeit \(x(t)\). Die Geschwindigkeit ist die Veränderung der Position pro Zeit, d.h. die erste zeitliche Ableitung (\(\frac{d}{dt}\)) von \(x\). In der Physik wird die zeitliche Ableitung mit einem Punkt geschrieben, um sie von der örtlichen Ableitung (\(\frac{d}{dx}\)) zu unterscheiden, die mit dem üblichen Apostroph-Stich notiert wird.
\[ v = \frac{d}{dt}x(t) = \dot{x}(t)\]
Die Beschleunigung ist dann die Veränderung der Geschwindigkeit mit der Zeit, d.h. wir leiten nochmals ab:
\[ a = \frac{d^2}{dt^2} x(t) = \ddot{x}(t) \]
Wir setzen das in Newtons Zweites Gesetz ein und erhalten:
\[ F = m \cdot \ddot{x}(t) \]
Verantwortlich für die Kraft \(F\) ist die Feder und gemäss Hooke’schem Gesetz gilt, dass die Kraft gleich der Federkonstanten mal die Auslenkung der Feder ist. Wir setzen das negative Vorzeigen, weil die Kraft bei einer Auslenkung von \(x\) z.B. nach rechts, immer entgegengesetzt zeigt, d.h. in diesem Beispiel nach links:
\[ F = -k \cdot x(t) \]
Wir setzen beide Ausdrücke für \(F\) gleich und erhalten die folgende Gleichung, die eine sog. Differentialgleichung ist, denn sie beinhaltet eine unbekannte Funktion \(x(t)\) und deren Ableitungen:
\[ m \cdot \ddot{x}(t) = -k \cdot x(t) \]
\[ \ddot{x}(t) = -\frac{k}{m} \cdot x(t) \]
Jetzt kommt ein kleiner Kunstgriff, der aber bald klar sein wird. Wir substituieren den Bruch mit \(\omega_0^2\) und erhalten eine schöne einfache Differentialgleichung:
\[ \omega_0^2 = \frac{k}{m} \]
\[ \ddot{x}(t) = -\omega_0^2 \cdot x(t) \]
Differentialgleichungen können nicht einfach gelöst werden. Man muss die Lösungen gewissermassen ”erraten”. Wir wählen dazu einen sog. Ansatz für \(x(t)\) und schauen, ob er die Differentialgleichung erfüllt.
Da wir eine Schwingung erwarten, liegt der folgende Ansatz für die Position der Masse nahe:
\[ x(t) = A \cdot \sin(\omega_0 t) \]
Die Ableitungen sind:
\[ \dot{x}(t) = \omega_0 \cdot A \cdot \cos(\omega_0 t) \]
\[ \ddot{x}(t) = -\omega_0^2 \cdot A \cdot \sin(\omega_0 t) \]
\[ \ddot{x}(t) = -\omega_0^2 \cdot x(t) \]
Jetzt sehen wir, dass unser Ansatz die Differentialgleichung erfüllt! Er ist also unsere Lösung:
\[ x(t) = A \cdot \sin(\omega_0 t) \quad \text{mit} \quad \omega_0=\sqrt{\frac{k}{m}} \]
Es ist eine harmonische Schwingung mit der Eigenfrequenz \(\omega_0\). Wenn wir die Feder steifer wählen (grösseres \(k\)), erhöht sich die Eigenfrequenz. Wenn wir die Masse \(m\) vergrössern, wird die Eigenfrequenz kleiner und das System schwingt langsamer (träger).
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.