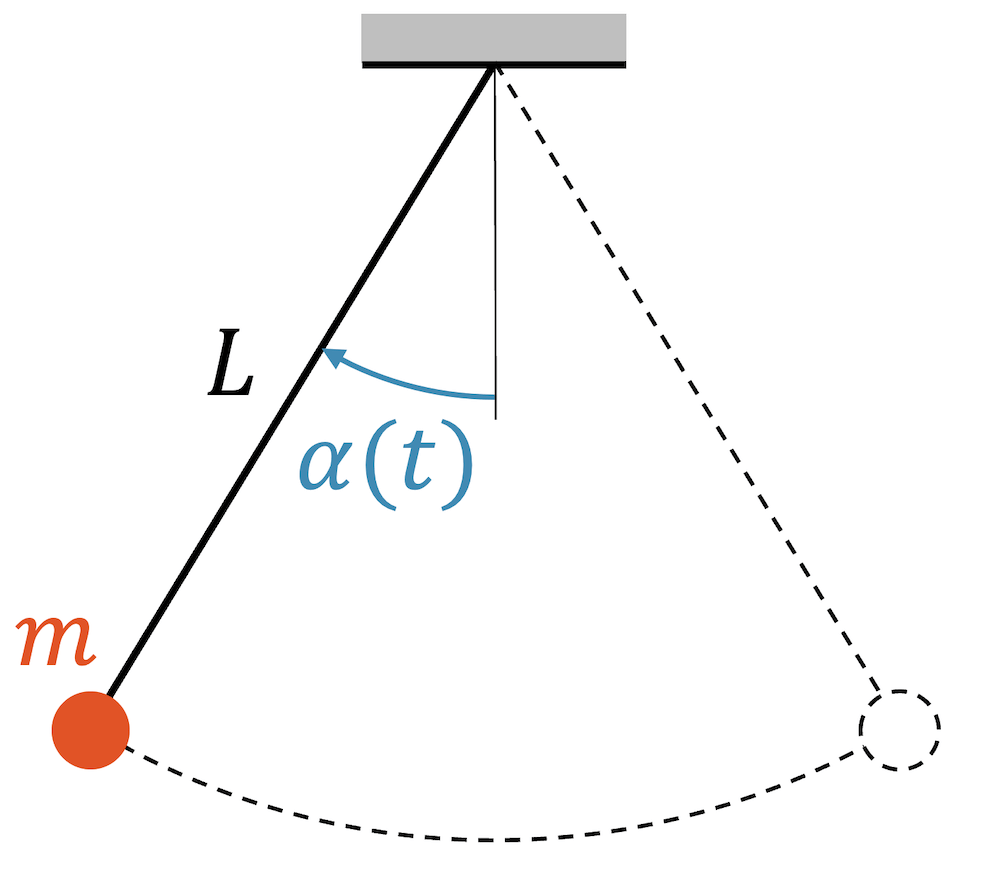
Das Fadenpendel ist ein wichtiger Typ von Schwingungssystemen, bei welchem die Rückstellkraft durch die Erdanziehung, d.h. durch die Gewichtskraft gegeben ist. Die schwingende Grösse ist die Höhe der Masse \(h\), meist wird jedoch der Auslenkungswinkel \(\alpha(t)\) als schwingende Grösse genommen.
Ein Schwingungssystem mit einem schwingenden Faden oder Arm kann als Fadenpendel verstanden werden. Die Rückstellkraft ist proportional zur Gewichtskraft und somit zur Masse (und Erdbeschleunigung).
Die Eigenfrequenz eines solchen Schwingungssystems ist hauptsächlich abhängig von der Fadenlänge \(L\), nicht aber von der Masse \(m\):
\[ \omega_0 = \sqrt{\frac{g}{L}} \]
Natürlich ist jedes Pendel, z.B. bei einer Wanduhr, ein Fadenpendel. Kinder auf der Schaukel bilden im physikalischen Sinn auch ein Fadenpendel. Da wird auch klar, dass die Masse des Kinds keine Rolle spielt. Kleine und auch grosse Kinder, selbst Erwachsene werden auf einer Schaukel immer mit der gleichen Frequenz schaukeln, da in beiden Fällen \(L\) und \(g\) gleich sind.
Herleitung der Schwingungsfunktion
Wenn wir einen beliebigen Winkel \(\alpha\) nehmen, können wir die senkrecht wirkende Gewichtskraft in zwei Komponenten \(F_{g\perp}\) und \(F_{g\parallel}\) aufteilen.
Die Teilkraft \(F_{g\perp}\) steht senkrecht zur Bewegung der Masse. Sie zeigt in Richtung des Fadens. Der Faden oder das Seil ziehen als Reaktion mit gleichem Betrag zurück (Newtons Drittes Gesetz). Diese Kraft wirkt deshalb nicht als Rückstellkraft.
Die zweite Komponente \(F_{g\parallel}\) ist hingegen die Rückstellkraft. Sie wirkt “gegen die Auslenkung” \(\alpha\) und versucht sie wieder zu korrigieren, was eine Rückstellkraft typischerweise tut.
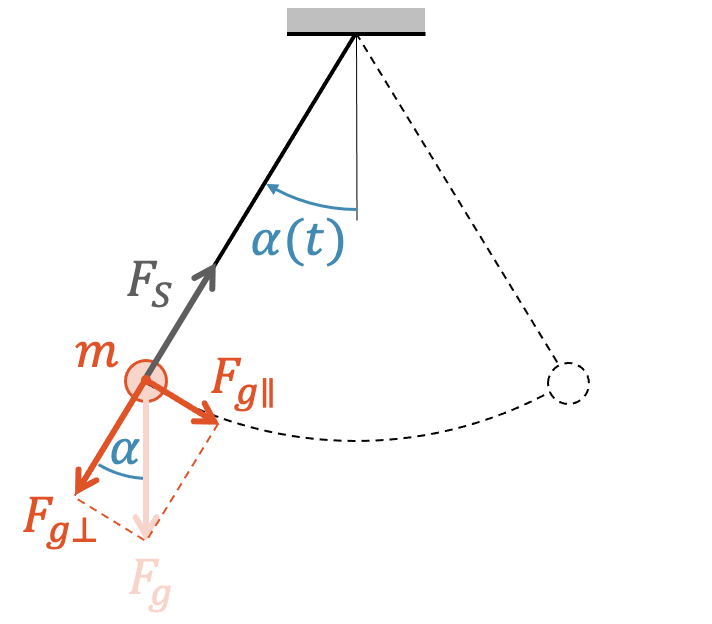
Aus einfachen trigonometrischen Betrachtungen heraus, können wir schreiben:
\[ F_{g\parallel} = F_g \cdot \sin(\alpha) \]
Beachte, dass für die Gleichgewichtsposition in der Mitte (\(\alpha = 0\)) wir keine Rückstellkraft haben, weil dann die Gewichtskraft zu 100% von der Fadenkraft kompensiert wird.
Ist die Masse einmal ausgelenkt, wirkt die Rückstellkraft beschleunigend, d.h. wir benutzen Newtons Zweites Gesetz:
\[ F_{g\parallel} = m \cdot a \]
Darauf folgt:
\[ \require{cancel} a = \frac{F_{g\parallel}}{m} = \frac{F_g \cdot \sin(\alpha)}{m} = \frac{\cancel{m}g \cdot \sin(\alpha)}{\cancel{m}} \]
Die Masse \(m\) hat sich hier heraus gekürzt – mehr dazu später. Das Ende des Fadenpendels beschreibt eine Kreisbahn, d.h. wir können für die Bahngeschwindigkeit \(v\) schreiben:
\[ v = L \cdot \omega \]
Dabei ist die Länge des Fadens \(L\) der Radius unserer Kreisbahn und \(\omega\) ist die Winkelgeschwindigkeit der Kreisbewegung. Die Winkelgeschwindigkeit ist ja nichts anders als die Änderung des Winkels mit der Zeit:
\[ \omega = \frac{\Delta \alpha}{\Delta t} = \frac{\text{d}}{\text{dt}}\alpha(t) \]
Für die Beschleunigung brauchen wir nur die Geschwindigkeit mit der Zeit abzuleiten, weil sie ja die Änderung der Geschwindigkeit mit der Zeit ist:
\[ a = \frac{\text{d}}{\text{dt}} v = \frac{\text{d}}{\text{dt}} \Big( L \cdot \omega \Big) \]
\[ a = \frac{\text{d}}{\text{dt}} \Big( L \cdot \frac{\text{d}}{\text{dt}}\alpha(t) \Big) = L \cdot \ddot{\alpha}(t) \]
Der Winkel \(\alpha\) hat in der Zeichnung oben eine Richtung (nach links). Wir müssen das so verstehen: Wenn der Winkel zunimmt, dann bewegt sich die Masse nach links. Die Beschleunigung aufgrund der Kraft wäre aber, wenn schon, nach rechts gerichtet. Wenn wir also von der gleichen Beschleunigung \(a\) reden möchten, müssen wir ein Minuszeichen einführen:
\[ a = -\frac{F_{g\parallel}}{m} = -L \cdot \ddot{\alpha} \]
Wir können jetzt die Beschleunigung \(a\) ersetzen mit dem Ausdruck \(a=g \cdot \sin(\alpha)\) von oben und erhalten eine sog. Differentialgleichung:
\[ g \cdot \sin\Big(\alpha(t)\Big) = -L \cdot \ddot{\alpha}(t) \]
Die Lösung dieser Differentialgleichung sind alle Funktionen \(\alpha(t)\), die die Schwingung eines Fadenpendels beschreiben. Das Problem ist, dass das eine nicht-lineare Differentialgleichung ist und die ist so eigentlich gar nicht lösbar. Wir müssen deshalb eine Vereinfachung vornehmen.
Für kleine Winkel \(\alpha\) gilt die lineare Approximation der Sinus-Funktion:
\[ \sin(\alpha) \approx \alpha \]
Die Differentialgleichung wird zu:
\[ g \cdot \alpha(t) = -L \cdot \ddot{\alpha}(t) \]
Wir dividieren durch \(L\) und erhalten:
\[ \ddot{\alpha}(t) = -\frac{g}{L} \cdot \alpha(t) \]
Beachte, dass die folgende Differentialgleichung sehr einfach lösbar ist:
\[ \ddot{\alpha}(t) = -\omega_0^2 \cdot \alpha(t) \]
Die Lösungen sind nämlich die Sinus- bzw. Kosinusfunktion, die beide das Gleiche repräsentieren, bis auf eine Phasenverschiebung von 90°. Mit dem Ansatz \(\alpha(t) = A \cdot \sin(\omega_0 t)\) sehen wir schnell, dass wir diese Lösung auf beiden Seiten der Differentialgleichung einsetzen können und die Differentialgleichung erfüllt wäre!
Damit gilt für die Eigenfrequenz der harmonischen Schwingung:
\[ \omega_0 = \sqrt{\frac{g}{L}} \]
Die allgemeine Lösung der Differentialgleichung ist somit:
\[ \alpha(t) = A \cdot \sin(\omega_0 t) \]
Je grösser die Länge des Fadens, desto kleiner ist die Eigenfrequenz dieser Schwingung. Unsere Erdbeschleunigung ist zwar fast eine Konstante, aber auf einem anderen Planeten oder auf dem Mond wäre das anders. Ein Pendel schwingt auf dem Mont deutlich langsamer, weil die Rückstellkraft kleiner ist.
Erstaunlich ist auch, dass die Eigenfrequenz von der Masse unabhängig ist! Das hat damit zu tun, dass die Gewichtskraft z.T. als Rückstellkraft wirkt. Diese Rückstellkraft ist bei doppelter Masse zwar doppelt so gross ist. Für eine gleiche Beschleunigung der Masse muss sie auch doppelt so gross sein! (Newtons Zweites Gesetz)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.