
Ein schwingfähiges System, d.h. mit Rückstellkraft und Trägheit kommt dann in Schwingung, wenn ihm Energie zugeführt wird. Diese Energie steht meistens in einer bestimmten Energieform bereit. Durch das Schwingen wird die Energie in eine andere Energieform umgewandelt.
Bei mechanischen Systemen ist das meistens kinetische Energie, d.h. etwas kommt in Bewegung. Nach dem Überschwingen bremst das System wieder ab und die kinetische Energie wird wieder in eine andere Energieform umgewandelt, meistens potenzielle Energie.
Ein Schwingungssystem kommt in Schwingung, wenn ihm Energie zugeführt wird. Diese Energie wird abwechselnd von der einen Energieform in die andere Energieform umgewandelt und wieder zurück.
Das System schwingt zwischen den beiden Energieformen hin und her. Die Summe der beiden Energieformen, die totale Energie \(E_{tot}\) bleibt aber konstant. Betragsmässig entspricht sie der anfänglich zugeführten Energiemenge.
Beispiel: Fadenpendel
Beim Fadenpendel schwingt eine Masse \(m\) an einem Faden der Länge \(L\) hin und her. Ein Pendel einer Wanduhr gilt auch als Fadenpendel, obwohl die Masse an einem Stift angemacht ist.
Das Fadenpendel schwingt nur, wenn wir die Masse anfangs etwas auslenken. Dadurch heben wir die Masse an und verrichten an ihr Hubarbeit. Sie erhält dadurch einen gewissen Betrag an potenzieller Energie \(E_{pot}\) und wir haben damit Energie in das Schwingungssystem eingebracht.
Sobald wir die Masse loslassen, fällt sie zurück zum tiefsten Punkt und wird durch den Fall beschleunigt. Potenzielle Energie wird dabei in kinetische Energie \(E_{kin}\) umgewandelt. Im tiefsten Punkt ist die potenzielle Energie komplett umgewandelt worden. Der gleiche Betrag steht jetzt als kinetische Energie zur Verfügung.
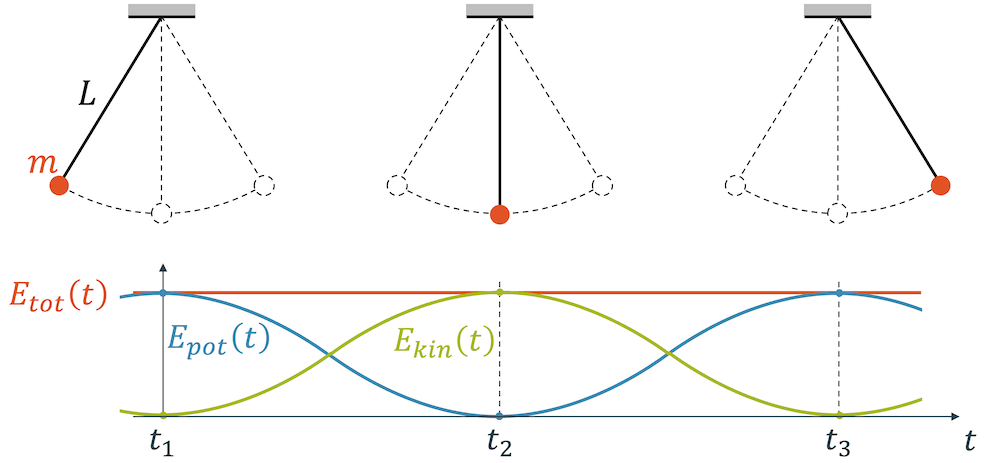
In Summe hat sich aber energetisch nicht geändert. Die totale Energie \(E_{tot}\) ist immer noch gleich gross wie zu Anfang, als sie zu 100% aus der potenziellen Energie der anfänglichen Auslenkung bestand. Die einzelnen Energieformen \(E_{pot}\) und \(E_{kin}\) schwingen ihrerseits hoch und runter. Die Energiesumme \(E_{tot}\) ist aber konstant.
Sobald die Schwingung einer gewissen Reibung unterliegt, wird ein Teil der Energie mittels Reibungsarbeit in Wärme (thermische Energie) umgewandelt, die an der Schwingung nicht mehr beiträgt. In so einem Fall haben wir eine abnehmende Amplitude, eine mit der Zeit abklingende Schwingung. Es handelt sich dann um eine gedämpfte Schwingung.
Beim Fadenpendel wird potenzielle Energie \(E_{pot}\) in kinetische Energie \(E_{kin}\) umgewandelt und umgekehrt. Die Summe der Energie \(E_{tot}\) bleibt im reibungslosen Fall konstant.
Beispiel: Federpendel
Die Analyse des Federpendels zeigt sehr schnell, wie ähnlich es mit dem Fadenpendel ist. Auch hier wechseln sich zwei Energieformen gegenseitig ab und die Summe der beiden Energieformen \(E_{tot}\) bleibt auch hier konstant.
Die eine Energieform ist wieder die kinetische Energie \(E_{kin}\) der Geschwindigkeit der Masse. Die andere Energieform ist die in der Feder gespeicherte Energie. Diese wird auch potenzielle Energie \(E_{pot}\) genannt, wobei sie aber nichts mit einer potenziellen Energie aufgrund einer Gravitationskraft zu tun hat.
Beim Federpendel ist die Rückstellkraft die Federkraft, gegen die wir die Masse auslenken. Wir verrichten dabei Spannarbeit und bringen so Energie ins System.
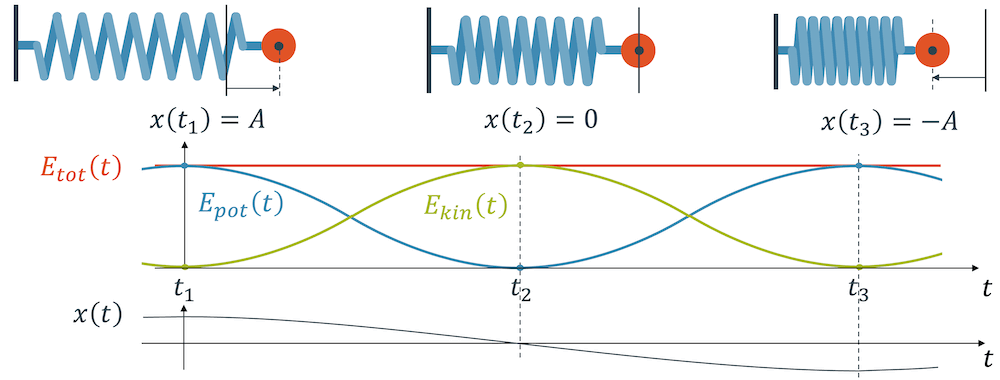
Beim Federpendel wird potenzielle Energie \(E_{pot}\) in der Feder (aufgrund von Federkraft) in kinetische Energie \(E_{kin}\) umgewandelt und umgekehrt. Die Summe der Energie \(E_{tot}\) bleibt im reibungslosen Fall konstant.
Schwingung der Energieformen
Wie wir beim Federpendel im obigen Bild festgestellt haben, schwingt die Energie mit der doppelten Frequenz gegenüber der sichtbaren Schwingung der Masse. Im obigen Bild sehen wir die Sequenz für eine halbe Periode des Federpendels. Wir müssten nochmals die Rückbewegung der Masse darstellen, um eine ganze Periode der Schwingungsbewegung zu haben.
Der Schwingungsverlauf der Energien hat aber die doppelte Frequenz bzw. die halbe Periode. Wir sehen, dass die potenzielle Energie in beiden Fällen maximal ist: Links bei voll gestreckter Feder und rechts bei voll gestauchter Feder.
Die Energien schwingen ebenfalls, jedoch mit doppelter Frequenz bzw. halber Periode gegenüber der Schwingungsbewegung.
Wir schauen uns die Sache jetzt analytisch an und nehmen dazu die Formel für die Berechnung der Spannarbeit an einer Feder von der Ausdehnung \(s_1\) zur Ausdehnung \(s_2\):
\[ W = \frac{1}{2}k s_2^2 – \frac{1}{2} k s_1^2 \]
Wir dehnen die Feder jetzt aber aus der Gleichgewichtslage (entspannt) zur allgemeinen Position \(x(t)\):
\[ W = \frac{1}{2} k x^2(t) \]
Das ist die Arbeit \(W\), die an der Feder verrichtet worden ist, d.h. diese Energie hat die Feder erhalten. Sie speichert sie in Form von potenzieller Energie.
Für \(x(t)\) setzen wir eine allgemeine harmonische Schwingung ein:
\[ x(t) = A \cdot \sin(\omega t) \]
Da die Spannarbeit \(W\) vollends als potenzielle \(E_{\text{pot}}\) in der Feder gespeichert wird, schreiben wir:
\[ E_{\text{pot}}(t) = \frac{A^2 k}{2} \cdot \sin^2 (\omega t) \]
Für das Quadrat des Sinus’ setzen wir die folgende trigonometrische Identität ein:
\[ \sin^2(x) = \frac{1-\cos(2x)}{2} \]
Wir erhalten:
\[ E_{\text{pot}}(t) = \frac{A^2 k}{4} \cdot \Big ( 1 – \cos (2\omega t) \Big) \]
Ausmultipliziert erhalten wir:
\[ E_{\text{pot}}(t) = \frac{A^2 k}{4} – \frac{A^2 k}{4} \cdot \cos (2\omega t) \]
Die potenzielle Energie \(E_{\text{pot}}\) in der Feder des Federpendels oszilliert mit doppelter Frequenz \(2\omega\) und innerhalb des Intervalls:
\[ \Big[ 0, \frac{A^2 k}{2} \Big] \]
Sie wechselt sich mit der kinetischen Energie \(E_{\text{kin}}\) ab.
Wir die Schwingung gedämpft, wird ein Teil der Energie, die im schwingenden System “eingeschlossen” ist, immerzu ein bisschen in Form von Wärme abgeführt. Es entsteht der charakteristische Verlauf einer gedämpften Schwingung mit abnehmender Amplitude.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.