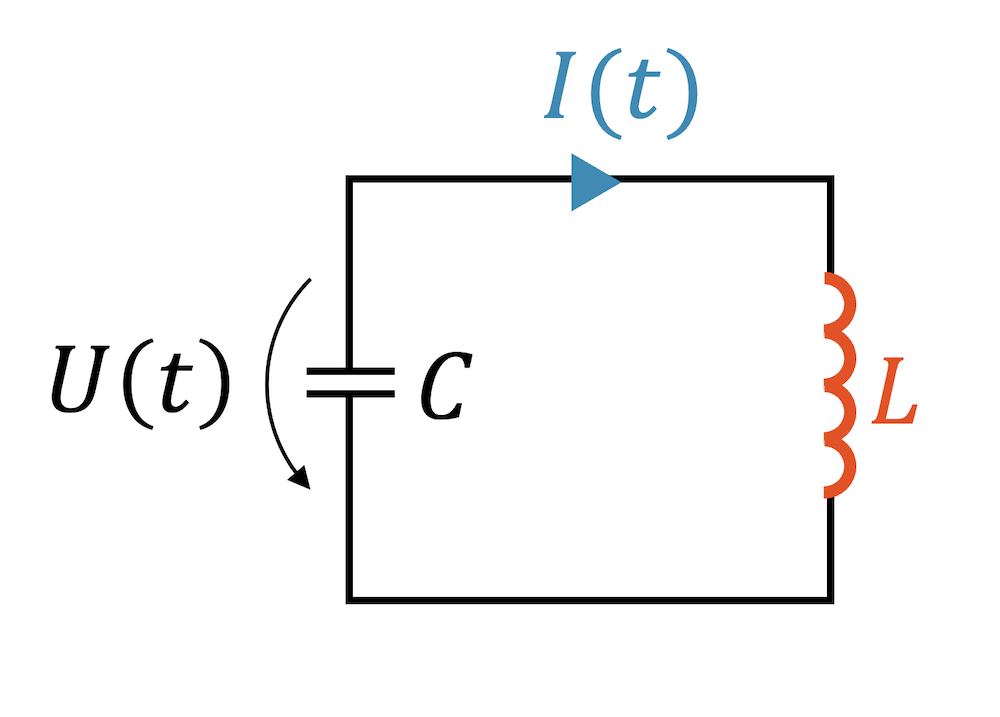
Der elektrische Schwingkreis ist ein nicht-mechanisches Schwingungssystem, bei welchem die Spannung \(U\) oder der elektrische Strom \(I\) mit einer Eigenfrequenz \(\omega_0\) schwingt. Bei vernachlässigbarem elektrischen Widerstand schwingt der elektrische Schwingkreis harmonisch:
\[ U(t) = U_0 \cdot \sin(\omega_0 t) \]
\[ I(t) = I_0 \cdot \sin(\omega_0 t) \]
Die Eigenfrequenz eines solchen Schwingkreises wird durch die Selbstinduktivität \(L\) der Spule und durch die Kapazität \(C\) des Kondensators bestimmt:
\[ \omega_0 = \frac{1}{\sqrt{LC}} \]
Elektrische Schwingkreise werden oft auch Resonanzkreise genannt, denn die Eigenfrequenz, mit welcher sie schwingen, auch ihrer Resonanzfrequenz entspricht.
Aufgebaut wird ein elektrischer Schwingkreis mit einer Spule der Selbstinduktivität \(L\) und einem Kondensator der Kapazität \(C\). Die Energie, die im Schwingkreis steckt, wechselt zwischen der Spule und dem Kondensator. Die Ladungen fliessen dazu hin und her und bauen im Kondensator ein elektrisches Feld auf und ab und in der Spule ein magnetisches Feld. Dieses Auf- und Entladen geschieht durch einen Wechselstrom \(I(t)\).
Die Anwendungen solcher Schwingkreise sind sehr vielfältig. Einerseits werden sie gebraucht, um Wechselströme bzw. -spannungen einer bestimmten Frequenz zu erzeugen.
Andererseits eignen sie sich gut als Frequenzfilter, denn ein Schwingkreis kommt nur dann in Resonanz, wenn er mit seiner Eigenfrequenz angeregt wird. Stimmt die Frequenz nicht, kommt er nicht in Fahrt. Der Schwingkreis kann so auf eine bestimmte Frequenz eingestellt werden, auf welche er reagieren wird. Die anderen Frequenzen wird er ignorieren. In der Funktechnik wird das ausgenutzt, um z.B. ein einzelnes Signal zu empfangen, das auf einer bestimmten Frequenz moduliert worden ist.
Herleitung der Schwingungsfunktion
Wir wissen, dass ein Strom durch eine Spule ein magnetisches Feld im Inneren der Spule aufbaut. Wenn wir diesen Strom ändern, ja sogar oszillieren lassen, dann wird auch das magnetische Feld auf- bzw. abgebaut und der magnetische Fluss nimmt zu oder ab. Aus dem Induktionsgesetz folgt, dass ein sich ändernder magnetischer Fluss eine elektrische Spannung induziert.
Zusammengefasst: Die zeitliche Änderung des Stroms durch die Spule bewirkt eine Spannung. Für die Spule gilt:
\[ U = -L \cdot \frac{\text{d}I}{\text{dt}} = -L \cdot \dot{I} \]
Das Minuszeichen ist beim Induktionsgesetz üblich, da die induzierte Spannung \(U\) gewissermassen der Richtung des Strom \(I\) entgegengesetzt ist (Lenz’sche Regel). Der Strom \(I\) ist die Ladung \(Q\), die pro Zeit \(t\) fliesst. Wir schreiben deshalb:
\[ I = \frac{\Delta Q}{\Delta t} = \frac{\text{d}Q}{\text{dt}} \]
Die im Kondensator gespeicherte Ladung \(Q\) ist der Spannung \(U\), die am Kondensator anliegt, proportional, mit dem Proportionalitätsfaktor \(C\), der die Kapazität des Kondensators bemisst:
\[ Q = C \cdot U \]
Wenn wir das oben einsetzen wollen, brauchen wir die zeitliche Ableitung der Ladung. Dazu leiten wir einfach beide Seiten der Gleichung nach der Zeit \(t\) ab und behandeln die Kapazität \(C\) als Konstante, da sie sich mit der Zeit nicht ändert:
\[ \dot{Q} = C \cdot \dot{U} \]
Jetzt setzen wir das oben in den Ausdruck für \(I\) ein:
\[ I = \dot{Q} = C \cdot \dot{U} \]
Jetzt nehmen wir den Ausdruck, den wir oben für die Spannung erhalten haben, leiten ihn nach der Zeit ab und setzen ihn in diese Gleichung für den Strom \(I\) ein.
\[ U = -L \cdot \dot{I} \]
\[ \dot{U} = -L \cdot \ddot{I} \]
\[ I = C \cdot \dot{U} = C \cdot (-L \cdot \ddot{I}) \]
Dividiert durch \(C\) und \(L\) und die Seiten vertauscht, erhalten wir die Differentialgleichung für den Strom \(I(t)\):
\[ \ddot{I}(t) = -\frac{1}{LC} \cdot I(t) \]
Welche Funktion ergibt sich selbst mit einem negativen Vorzeichen? Die Sinus- und die Konsinusfunktion haben diese Eigenschaft! Wir nehmen deshalb den Ansatz \(I(t) = I_0 \cdot \sin(\omega_0 t)\) und erhalten:
\[ \ddot{I}(t) = -\omega_0^2 \cdot I(t) \]
Die Differentialgleichung ist erfüllt, wenn
\[ \omega_0^2 = \frac{1}{LC} \]
\[ \omega_0 = \frac{1}{\sqrt{LC}} \]
Der Strom \(I(t)\) schwingt harmonisch mit der Eigenfrequenz \(\omega_0\), die je grösser \(L\) und \(C\) sind, umso kleiner ausfällt. Das erscheint uns intuitiv richtig, denn wenn wir einen sehr grossen Kondensator und eine sehr grosse Spule nehmen, dann muss soviel Ladung hin und her bewegt werden, dass das nicht ganz so schnell gehen kann und die Eigenfrequenz deshalb klein sein muss.
Wir können mit der Wahl des Kondensators und der Spule die gewünschte Eigenfrequenz des Schwingkreises einstellen.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.