
Die Rotationsenergie ist die kinetische Energie der Masse eines Körpers, der um seinen Schwerpunkt rotiert. Bei einer allgemeinen Bewegung besteht die kinetische Energie aus einem translatorischen Anteil, der durch die Bewegung des Schwerpunkts entsteht und einem Rotationsanteil, der Rotationsenergie genannt wird.
Die Rotationsenergie berechnet sich aus dem Trägheitsmoment \(I\) und der Winkelgeschwindigkeit \(\omega\):
\[ E_{rot} = \frac{1}{2} \; I \; \omega^2 \]
Dabei wird eine Analogie zur translatorischen kinetischen Energie \(E_{kin} = \frac{1}{2} m v^2\) offensichtlich, in welcher das Trägheitsmoment die Rolle der Masse übernimmt.
Die Rotationsenergie ist unbedingt vom Drehimpuls zu unterscheiden, der mit der Energie zwar verknüpft ist, jedoch eine eigene Erhaltungsgrösse darstellt.
Definitionen
Abkürzung: \(E_{rot}\)
Einheit: \([\,E_{rot}\,] = \text{J}\) (Joule)
Herleitung
Bei der Diskussion der kinetischen Energie haben wir gelernt, dass eine Masse \(m\), die sich mit einer Geschwindigkeit \(v\) bewegt, kinetische Energie besitzt:
\[ E_{kin} = \frac{1}{2}mv^2 \]
Was passiert aber, wenn sich der Körper mit der Masse \(m\) nicht bewegt (\(v=0\)), sondern um seine eigene Achse rotiert. Da der Schwerpunkt in Ruhe ist, erhalten wir mit der obigen Gleichung eine kinetische Energie, die null ist! Ein rotierender Körper hat aber sicherlich mehr Energie als ein nicht rotierender Körper. Ein Jo-Jo kann sich z.B. an seiner eigenen Schnur wieder hochwickeln und damit die vorhandene Energie in potentielle Energie umwandeln. Ein nicht-rotierendes Jo-Jo könnte das nicht. Die Energie eines rotierenden Körpers um seinen Schwerpunkt heisst Rotationsenergie.
Das Problem entsteht, weil die Masse des Körpers in einem Punkt konzentriert wird, dem Schwerpunkt. Das ist für die meisten Bewegungen sehr praktisch. Für die Rotation um den eigenen Schwerpunkt verlieren wir aber jegliche Information über die Energie, da ein rotierender, unendlich kleiner Punkt nicht von einem nicht-rotierenden Punkt unterschieden werden kann.
Betrachten wir deshalb die Masse \(m\) in zwei Punkte aufgeteilt, je mit der Masse \(\frac{1}{2}m\) ausgestattet und im Abstand \(r\) vom Drehzentrum.
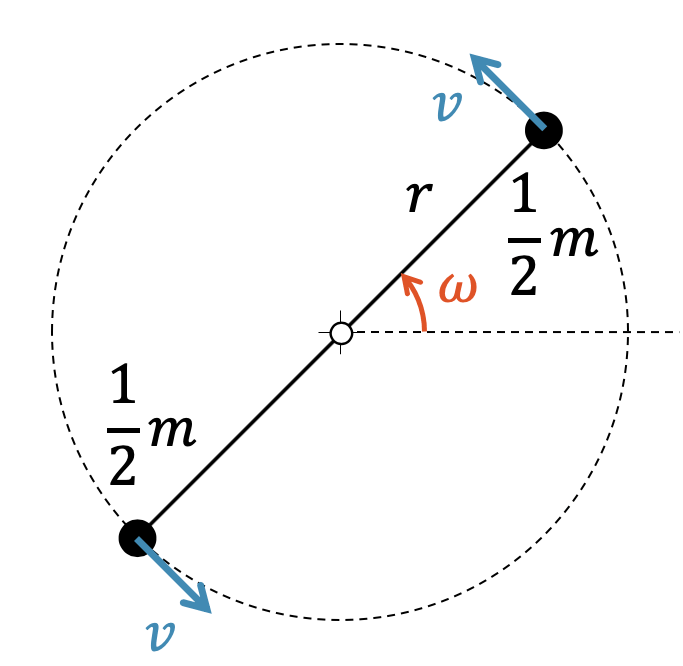
Wir können jetzt den beiden Massen je eine kinetische Energie zuordnen, denn sie sind auf einer Kreisbahn und haben die Geschwindigkeit \(v\). Die Rotationsenergie des Zwei-Masse-Systems ist somit die Summe der kinetischen Energien für zwei Teilmassen. Beachten Sie auch, dass die beiden Teilmassen nur \(\frac{m}{2}\) betragen:
\[ E_{rot} = 2 \cdot \frac{1}{2}\Big(\frac{m}{2}\Big)v^2 = \frac{1}{2}mv^2 \]
Wir setzen jetzt für die Geschwindigkeit den Ausdruck \(v=r \omega\) ein:
\[ E_{rot} = \frac{1}{2} m \cdot (r \omega)^2 = \frac{1}{2} m r^2 \omega^2 \]
Aus einer Tabelle entnehmen wir, dass ein Körper der Masse \(m\) in einem Abstand \(r\) ein Trägheitsmoment \(I = mr^2\) hat. Wir setzen diesen Ausdruck oben ein und erhalten für die Rotationsenergie:
\[ E_{rot} = \frac{1}{2} \Big(m r^2\Big) \omega^2 = \frac{1}{2} \; I \; \omega^2 \]
Beachten Sie die Analogie zum Ausdruck der (translatorischen) kinetischen Energie:
\[ E_{rot} = \frac{1}{2} \; I \; \omega^2\quad \quad \leftrightarrow \quad \quad E_{kin} = \frac{1}{2} \; m \; v^2 \]
Die für die Trägheit verantwortliche Masse \(m\) wird bei einer Rotation durch das Trägheitsmoment \(I\) ersetzt. Statt der Geschwindigkeit \(v\) haben wir die Winkelgeschwindigkeit \(\omega\). Wir können von nun an unser Verständnis für die kinetische Energie damit erweitern, dass für jede allgemeine Bewegung eines Körpers, die kinetische Energie aus einem translatorischen Anteil aus der geradlinigen Bewegung des Schwerpunkts \(v\) und einem Anteil aus der Rotationsbewegung \(\omega\) besteht.
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.