Wilhelm Conrad Röntgen (1845 – 1923) war ein deutscher Physiker, der 1868 sein Studium als Maschineningenieur an der ETH Zürich abschloss. Im Jahre 1895 entdeckte er die nach ihm benannten Röntgenstrahlen. Seine Apparatur hatte die Strahlen erzeugt, zuerst noch unbemerkt, da für den Menschen nicht sichtbar. Er fand dann aber heraus, dass seine Fotoplatten offenbar durch eine unsichtbare Strahlung belichtet worden waren.
Image, public domain
Heutzutage sind Röntgenstrahlen nicht mehr wegzudenken. Sie haben eine ausserordentliche Bedeutung in der Medizin, aber auch in der Astronomie, Materialforschung und -analyse. Auch in der Biochemie werden Röntgenstrahlen für die Kristallographie von Proteinen eingesetzt.
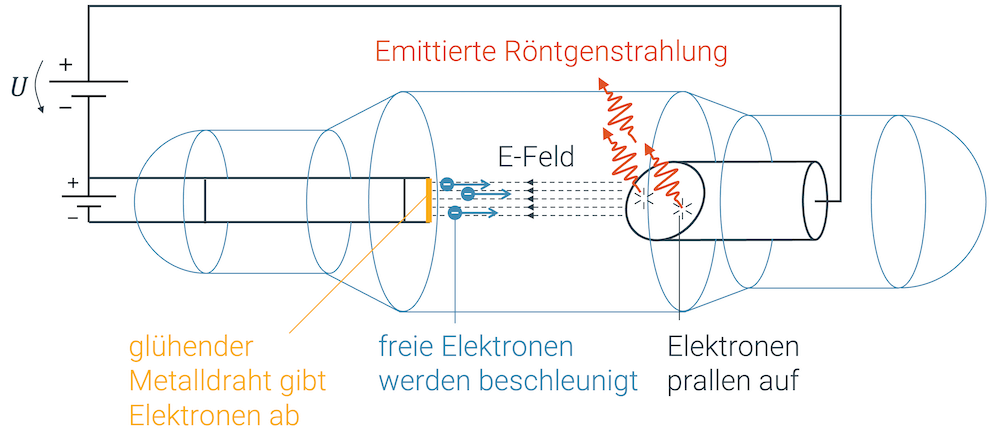
Die von Röntgen entwickelte Röntgenröhre besteht aus einem evakuierten Glasrohr in welchem auf der einen Seite ein glühender Metalldraht (Kathode) angebracht ist. Auf der anderen Seite steht die Anode, die durch eine Anschrägung die Röntgenstrahlen nach aussen leitet. Zwischen Kathode und Anode wird eine hohe Spannung \(U\) angebracht. Die Kathode wird an den negativen Pol und die Anode an den positiven Pol angeschlossen.
Wegen der hohen Temperatur im Glühdraht, werden Elektronen aus dem Glühdraht ”herausgeschüttelt”. Die Energie der Gitterbewegung ist so stark, dass sie gewisse Metallatome ionisieren vermag, d.h. einzelne Elektronen werden herausgeschlagen. Diese nunmehr freien Elektronen befinden sich jetzt im elektrischen Feld zwischen Kathode und Anode und werden mit der Coulombkraft zur Anode hin angezogen bzw. beschleunigt.
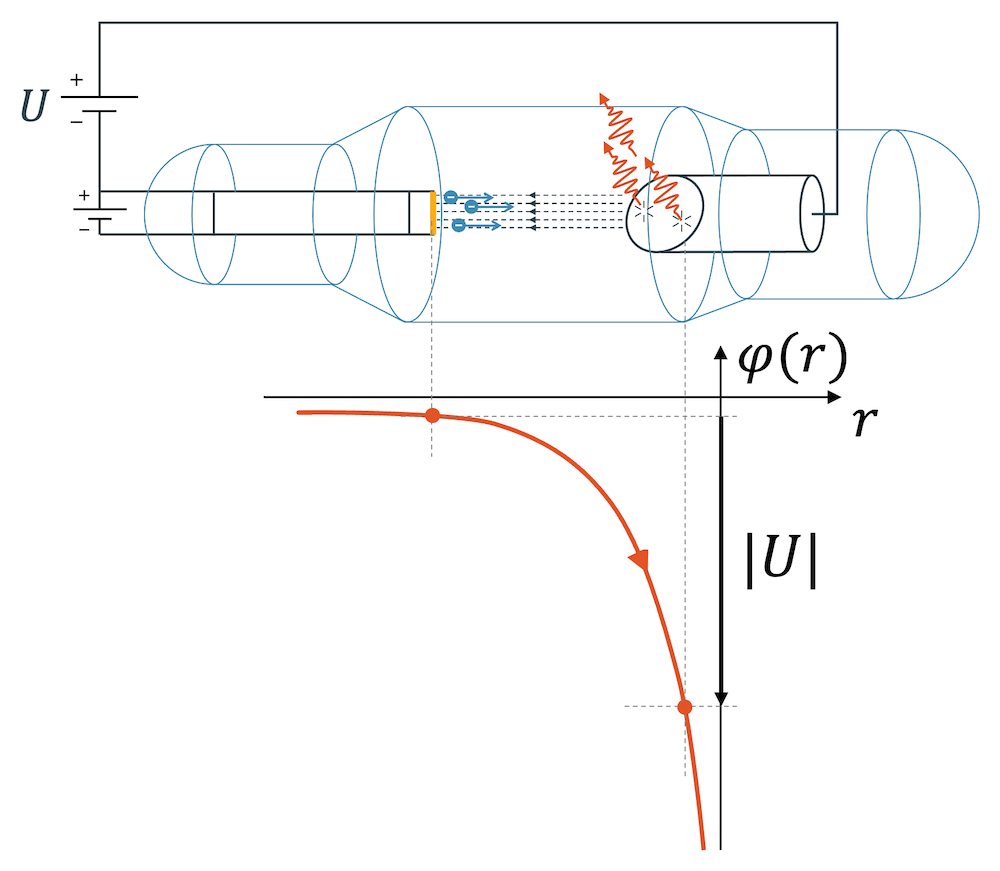
Wir können mit Hilfe des elektrischen Potenzials uns vorstellen, dass die Elektronen der Kathode gegenüber der Anode mit Energie ”aufgeladen” sind. Sie sind gewissermassen auf einer hohen Klippe und fallen hinunter. Die angelegte Spannung \(U\) bestimmt die Differenz zwischen dem Potenzial der Kathode und dem der Anode. Die Spannung macht gewissermassen die Höhe der Klippe aus. In der Röntgenröhre ist diese Spannung sehr hoch (ein paar Kilovolt) und die Elektronen der Kathode sind damit gegenüber der Anode sehr stark ”aufgeladen”. Einmal aus dem Glühdraht befreit, werden sie sehr stark beschleunigt und prallen mit grosser kinetischer Energie auf die Anode.
Durch den Aufprall wird die kinetische Energie der Elektronen in Wärme und Strahlung umgewandelt. Moderne Röntgenröhren haben deshalb meistens eine rotierende Scheibe als Anode. So kann der eben beschossene Teil wegrotiert und gekühlt werden.
Beispiel
Wie viel beträgt die kinetische Energie eines Elektrons, das in einer Röntgenröhre mit einer Spannung \(U = 2\,\text{kV}\) beschleunigt wurde und wie gross ist die Geschwindigkeit beim Aufprall auf der Anode?
Ladung des Elektrons: \(q_e = 1.602 \cdot 10^{-19}\,\text{C}\)
Masse des Elektrons: \(m_e = 9.109 \cdot 10^{-31}\,\text{kg}\)
Wir nehmen die Definition der Spannung und formen sie nach der Energiedifferenz auf:
\[ U = \frac{\Delta E_{pot}}{q_e} \qquad \rightarrow \qquad \Delta E_{pot} = q_e \cdot U \]
Da die potenzielle Energie des Elektrons vollständig in kinetische Energie umgewandelt wird, können wir schreiben und einsetzen:
\[ \Delta E_{kin} = \Delta E_{pot} = q_e \cdot U = 1.602 \cdot 10^{-19}\,\text{C} \cdot 2\,\text{kV} \]
\[ \Delta E_{kin} = 3.204 \cdot 10^{-16}\,\text{J} \]
Für die kinetische Energie können wir schreiben:
\[ \Delta E_{kin} = \frac{1}{2} m_e v^2 \]
Wir lösen nach der Geschwindigkeit \(v\) auf und setzen Energie und Masse ein:
\[ v = \sqrt{\frac{2 \cdot \Delta E_{kin}}{m_e}} = \sqrt{\frac{2 \cdot 3.204 \cdot 10^{-16}\,\text{J}}{9.109 \cdot 10^{-31}\,\text{kg}}} = 2.65 \cdot 10^7\,\frac{\text{m}}{\text{s}} \]
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.



Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.